
| En Français | Home/Contact | Billiards | Hydraulic ram | HNS | Relativity | Botany | Music | Ornitho | Meteo | Help |

See Contents.
The site hosts several additional short and synthetic topics. See Contents.


Bardula is a pseudonym created by a Belgian artist who currently lives and works in France.
Bardula creates luminous paintings including the hypnotic paintings "Blue Interferences" and "Blue ice" (see Figures 1 and 2 above).
Sources :
Light ZOOM Lumière.
Bardula.






Here is a selection of the best motion illusions (see above Figure 1 cf. [GomboDigital], Figures 2 to 5 cf. [Sélection.ca] and Figure 6 cf. [Akiyoshi Kitaoka]) :
1. Rotating vortex (Vectordivider image via Getty Images)
2. Rotating spirals (Vectordivider image via Getty Images)
3. Mesmerizing effect (Mark Grenier image via Shutterstock)
4. Scroll (Guten Tag Vector image via Shutterstock)
5. Glitter Grid (Mark image via Shutterstock)
6. "Expanding pupils" (Image from Akiyoshi Kitaoka)
Sources :
Sélection du Reader's Digest (Canada) - 24 illusions d'optique complètement étourdissantes.
GomboDigital - 5 illusions d'optique qui vont vous scotcher/.
Akiyoshi Kitaoka - Anomalous motion illusions 35.




The Author of this site has made four wind sculptures installed in his garden in Berrac (Gers).
Description :
Design :
These sculptures are made with recycled products (aluminum rails for thermal insulation frame, PVC camping bowls, plastic jerrycan sides, tennis ball, rebar, etc.).
All moving parts are carried on ball bearings.
All the fixed elements are assembled by stainless steel screws.
The sculptures are fixed to the ground by a vertical mast (galvanized steel fence post or old steel water pipe).



Pierre Luu is a French sculptor who has created sculptures with unpredictable movements, driven by wind or water, including the "wind turbine with random motion" (see Figures above, and video "Mobile eolien art cinétique" in [Pierre Luu]).
Description :
Figure 1 above : general view (cf. [Art et Eau]).
Figure 2 above : zoom on blades twist angle (video clip 0:12).
Figure 3 above : zoom on blades lenght (video clip 0:22).
The "wind turbine with random motion" is made up of 5 moving parts in unstable equilibrium (cf. [Pierre Luu - Quelque chose ne tourne pas rond][Art et Eau - Quelque chose ne tourne pas rond]).
The balance is all the more unstable as there is no weather vane to orient the sculpture in the wind direction. The blue ball is aesthetic and symbolizes the Earth (cf. my email of March 5, 2023 from Pierre Luu to Régis Petit).
The two blades are of different size with a secondary rotation nested within the primary rotation (cf. [Pierre Luu - Eolide].
The sculpture slowly comes to life and changes shape thanks to the wind action. The movement is maintained by inertia due to the balance of the masses (cf. [Art et Eau - Quelque chose ne tourne pas rond]).
The sculpture unfolds in an enigmatic choreography and only finds temporary stability when the blades reach a certain speed (cf. [Pierre Luu - Quelque chose ne tourne pas rond]).
Design :
The whole is designed in a search for balance between the masses, the gravity centers, the surfaces exposed to the wind and the relative angles of the surfaces (cf. [Pierre Luu - Quelque chose ne tourne pas rond]).
The mobile elements are fixed by ball bearings for all sculptures in project version (cf. email of March 7, 2023 from Pierre Luu to Régis Petit). This combination allows fluid rotations and movements even in light winds (cf. [Pierre Luu - Fragments mobile éolien).
Material : stainless steel and composite materials (cf. [Art et Eau - Quelque chose ne tourne pas rond]).
Height : 3 m 50 (cf. [Art et Eau - Quelque chose ne tourne pas rond]).
Sources :
Pierre Luu - Mobile eolien art cinétique (YouTube, 01:57).
Pierre Luu - Un art en mouvement - Sculptures éoliennes et mobiles.
Pierre Luu - Un art en mouvement - Quelque chose ne tourne pas rond.
Pierre Luu - Un art en mouvement - Fragments mobile éolien.
Pierre Luu - Un art en mouvement - Eolide.
Pierre Luu - Un art en mouvement - Solaris : sculpture éolienne et solaire autonome en énergie.
Art et Eau - Ellipse, quelque chose ne tourne pas rond.



Jeff Kahn is an American sculptor who created kinetic sculptures, titled "Invisible Forces", from aluminum and stainless steel.
These sculptures explore balance and gravity and how almost imperceptible air currents interact with them. They are extremely sensitive to the surrounding environment (light breezes, sun heat, weight of the morning dew). See above Figures 1, 2 and 3 showing three particular sculptures : "Astrolabe", "Naked Alien" and "I Ching".
Jeff Kahn's studio is located in Lenhartsville, Pennsylvania, USA.
Sources :
Jeff Kahn - Bio.
Jeff Kahn - Catalog.
Jeff Kahn - Videos.



Anthony Howe is an American sculptor who has created hypnotic mobile sculptures including "Di-Octo" in 2014 (see Figures 1, 2 and 3 above, and "Di-Octo" video in [Anthony Howe] and [KULTT]).
Anthony Howe currently lives in Eastsound, Orcas Island, San Juan County, Washington State (USA).
Description :
Di-Octo is a half-octopus, half-star, wind-driven and near-silent mobile sculpture.
The original Di-Octo, designed and made by Anthony Howe, has been industrialized in two identical copies by Show Canada Inc (Laval steelworks in Quebec) as follows (cf. email of March 10, 2023 from David Boulay (Show Canada Inc) to Régis Petit) :
Design :
Di-Octo is 8 meters high, 3 meters in diameter, weighs 725 kilograms and requires only 2 km/h of wind for its moving parts to activate (cf. [Concordia University]).
Di-Octo is composed of 36 arms each carrying 16 very thin steel domes and rotating around a vertical circular ring. The inter-arm connections are of the intermediate wheel type with drive fingers. See detail in Figure 3 above (cf. [Show Canada]).
The arms always turn in the same direction, regardless of the wind direction. This is due to the domes shape (cf. email of March 19, 2023 from David Boulay to Régis Petit).
Di-Octo is entirely made of 316 stainless steel, which gives it better corrosion resistance as well as non-magnetic properties (cf. [Show Canada]).
Other similar sculptures :
Anthony Howe designed and made other sculptures similar to Di-Octo (cf. [Anthony Howe, https://www.howeart.net/about]) :
Sources :
Anthony Howe.
Anthony Howe - Shindahiku (Fern pull).
The DC Blike Blogger - Shindahiku (Fern Pull).
KULTT - Les sculptures hypnotiques d'Anthony Howe.
Anthony Howe - Di-Octo (Youtube 1:10).
Anthony Howe - Di-Octo (long version) (Youtube 1:33).
Université Concordia - Di-Octo : captivant, cinétique et unique.
Show Canada.
JuanG3D : Di-Octo 3D Model.
What's on - Check out these alien-esque kinetic sculptures in Dubai.
UAE - Famous American artist brings kinetic sculptures to Dubai.
reddit - "Octo II", Anthony Howe, stainless steel, 2013..


Jennifer Townley is a Dutch artist who has created hypnotic mobile sculptures including "Asinas" in 2015 (see Figure 1 above, and video "Asinas").
When viewed at a standstill from the front, it looks like a double helix like the usual representation of DNA.
Description (cf. [Jennifer Townley]) :
"Asinas" is a mobile sculpture composed of two helixes that intertwine and slide into each other, producing a fluid and natural movement.
The two helixes slowly rotate in opposite directions and at slightly different speeds, gradually transforming the sculpture.
A demonstration of how this sculpture works helps to better understand this description (see video "Asinas Working Demonstration" in [Amogh Jadhav] and video "SolidWorks Mechanical Sculpture" in [tecnoloxia.org]).
Design :
The sixty-five white wooden bricks that form the two helixes increase in size towards the middle of the sculpture, giving it a conical shape.
Each brick has the shape of a Z with 90 degree angles. The bricks of a helix are fixed on the rotation axis. The bricks of the other helix are connected to one another through small spacers (see Figure 2 above from [Amogh Jadhav]).
The bricks are made from painted wood. The frame is made of steel as well as all the parts connecting the gears to their axes, the bearings to the frame, etc.
Then there are all the other parts : an electric motor, heavy steel spur gears and sprockets, two belts and lots of bearings (cf. [The Plus Paper]).
Sources :
Asinas - Jennifer Townley - 2015 - Kinetic art (Youtube 2:31).
Jennifer Townley - Asinas.
L'Usine Nouvelle - Hypnotiques, ces sculptures cinétiques vous étonneront.
Amogh Jadhav - Asinas.
Amogh Jadhav - Asinas Working Demonstration (Youtube 2:14).
tecnoloxia.org - As esculturas cinéticas de Jennifer Townley.
MadCadSkills : Jennifer Townley - SolidWorks Mechanical Sculpture (Youtube 3:43).
The Plus Paper - Asinas : Fluent Movement ( http://www.thepluspaper.com/2015/03/23/asinas-fluent-movement/ ).
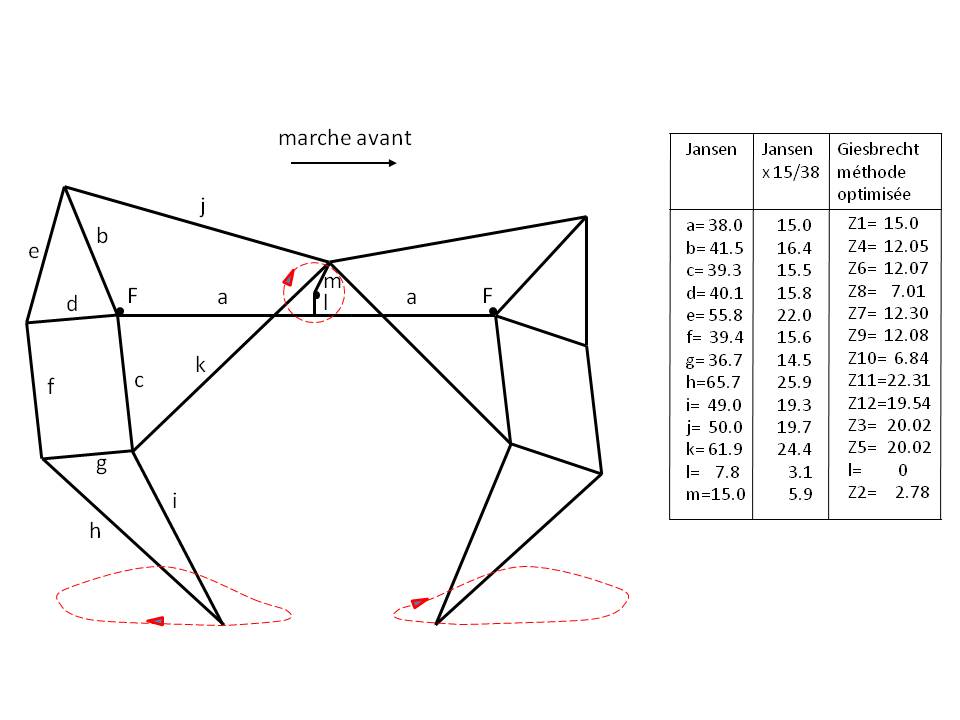
Theo Jansen is a Dutch sculptor who in 1991 created strange creatures including the walking robot (see Figures 1 and 2 above).
Working :
This walking robot is a mechanism with very light legs which can move on a horizontal plane under the wind action or on an inclined plane under the action of its own weight (see video cf. [Jansen, Plaudens Vela]).
The only actuator in the robot is a central crankshaft making the connection between the legs and the robot body (see red while on Figure 2, and also [Exergia]).
For a robot with three pairs of legs, the crankshaft has three cranks offset successively by 120° to have a constant movement of the robot during the propulsion phase (see Figure 2).
Body description :
The robot body consists of a horizontal platform (length 2a) and vertical fixed supports (length l) carrying the crankshaft (eccentricity m). See Figure 3 above.
The double length (a) of the platform is calculated to ensure non-collision between the front legs and the rear legs.
The length (l) of the supports can be modified to ensure an overall horizontal movement of the robot. Increasing or decreasing the length (l) amounts to pivoting all the bars of each leg around each fixed point F.
Legs description :
Each leg consists of ten articulated bars (bars b to k) of which two form a rigid link (bars e and h)). See Figure 3 above.
The two legs of the same pair are identical and mirror each other on each side of the crankshaft.
The foot of each leg describes an ovoid curve whose lower part is almost flat and horizontal, thus allowing the foot to be in contact with the ground during the propulsive phase.
In the return phase, the foot lifts off the ground and the robot can step over small obstacles without lifting its body too much.
The table of Figure 3 gives the length of each bar according to different authors :
Sources :
Jansen - Plaudens Vela.
Jansen - plaudens vela 1 (Youtube 0:53).
Wikipedia - Mécanisme de Jansen.
Exergia - Simulation von Theo Jansen's Strandbeest.
Giesbrecht Daniel - Design and optimisation of a one-degree-offreedom eight-bar leg mechanism for a walking machine.
The following files describe the monumental and architectural heritage of 140 municipalities located less than 20 km from the towns of Lectoure or Condom in Gers (France), and including Gers Lomagne and its surroundings.
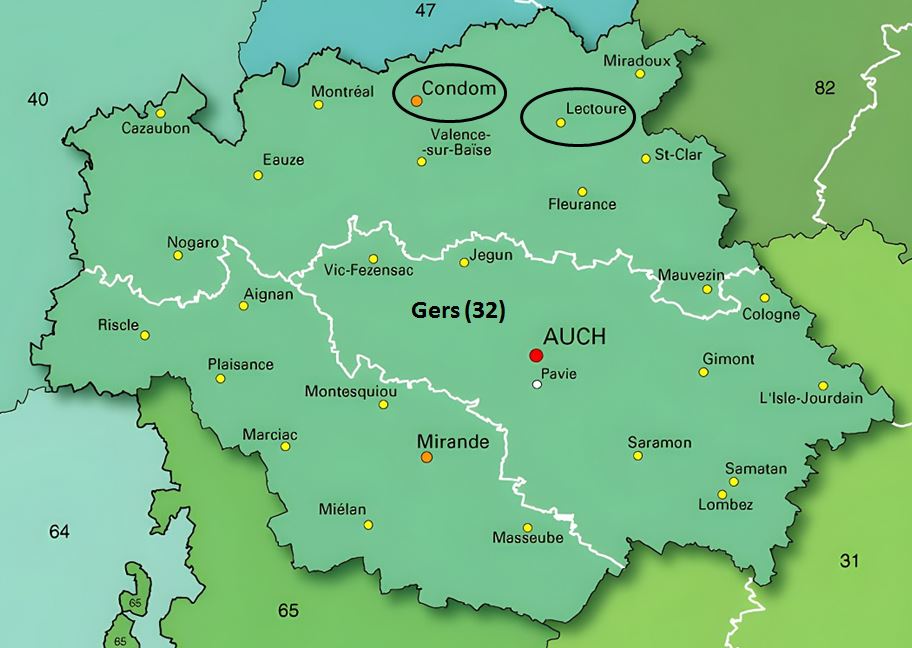
List of municipalities :
The municipalities are listed alphabetically, each followed by the department number: Gers (32 by default), Lot-et-Garonne (47), Tarn-et-Garonne (82).
Each pdf file weighs approximately 500 KB, the heaviest being Lectoure (3.3 MB).
Sources :
- Wikipedia, Descriptif de chaque commune dont département, toponymie, histoire, maire, nombre d'habitants, altitude, lieux et monuments.
- Ministère de la Culture, Immeubles protégés au titre des Monuments Historiques, par département et par commune. N'inclut pas les sites protégés.
- Ministères Ecologie Energie Territoires, Liste des servitudes des sites et monuments du Gers jusque janvier 2015, par commune et incluant la protection des sites et des monuments au titre des Monuments Historiques.
- SDAP renommé STAP (Services Territoriaux de l'Architecture et du Patrimoine), Liste des monuments historiques et des sites du Lot-et-Garonne, par commune et jusqu'en 2006.
- DREAL Midi-Pyrénées (Direction Régionale de l'Environnement, de l'Aménagement et du Logement Midi-Pyrénées), Bilan des sites classés et inscrits du Tarn-et-Garonne, avril 2013, par commune.
- Ministère de la Culture, Base Mérimée du patrimoine monumental français, par commune et par monument incluant date d'origine, lieu, descriptif et propriété.
- Comet Anaïs Villages et bourgs de la Gascogne gersoise à la fin du Moyen Age (1250-1550), par commune, Thèse d'histoire, 2017, Volume 1 : Synthèse (405 p), Volume 2 : Figures (442 p), Volume 3 : Notices (680 p), Volume 4 : Atlas (391 p).
- Google, Recherche par commune (histoire, origine du nom, bastide, castelnau, castrum, fortification, rempart, château, fossé, vestige) ou par monument (protection récente des monuments et des sites au titre des Monuments Historiques)
- Google Images et Google Vidéos, Recherche par commune (monument, "carte postale", vidéo Youtube).
- IGN (Institut Géographique National, renommé Institut National de l'information Géographique et forestière), Géoportail, par commune (situation graphique des lieux-dits et des rues).
- Google, Google Maps, par commune (situation GPS des lieux-dits, rues principales, photos par Street View).
- Google, Recherche par commune (cadrans solaires, moulins, pigeonniers, puits, fontaines, lavoirs).
- Mapio, Photos d'internautes avec titre et géolocalisation précise. Recherche par Région, Département, Arrondissement, Commune.
See detail.
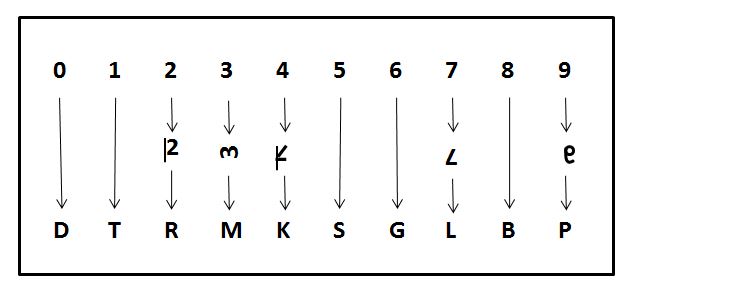

B4.1. Introduction :
Mnemonics encompasses all the techniques designed to facilitate the memorization and recall of information through mental associations.
Among these methods, the number articulation method [WIK] stands out for its effectiveness in remembering numbers. This system is based on a fixed correspondence between the numbers 0 to 9 and consonant sounds. For example, 3 corresponds to the sound "m". By freely adding vowels, sequences of numbers are transformed into concrete words that are easier to memorize. For example, the number 42 can become the word mouton (m = 3, t = 1).
The recall table of figures (from 0 to 9) was developed in the 19th century by Aimé Paris [PAR, p.28] and then adopted identically by Abbé François-Napoléon-Marie Moigno [WIK]. A different, simpler version was later proposed by Joe Bertin [BER] in 2028, and adopted almost identically by Régis Petit in 2025.
The recall table of numbers from 00 to 99 assigns a specific word to each of these numbers.
The steps of the number articulation method are as follows :
1. Associate each number from 0 to 9 with a consonant sound, according to a code to be memorized (see Recall table of figures).
2. Convert the sequence of numbers to be memorized into a sequence of sounds, according to this code.
3. Form a sequence of words from these sounds by adding vowels, so as to phonetically create a sentence, or mentally create a vivid and memorable story.
4. To reproduce the numbers, proceed in reverse : story, words, sounds, numbers.
Example of a story in French that you can create yourself to remember the first decimals of the number Pi = 3, 14 15 92 65 35 89 79 32 38... :
- According to the recall table of figures by Aimé Paris : "assis par TeRre sur une modeste ToiLe, je suis en PaNne et GèLe. Au loin, près d'une MeuLe de foin, se trouve une VamP portant une CaPe de MoiNe et des MouFles."
- According to the recall table of figures by Régis Petit : "sur mon TanK, à côté d'une TaSse, d'une PoiRe et d'une GouSse d'ail, j'écoute la MeSse, quand surgit un BiP sonore. J'éclaire avec ma LamPe et vois une MaRe avec un MeuBle en plein milieu."
Applications :
Among the applications where the number articulation method provides real benefits, we can cite :
- Telephone numbers encoded into 5 concrete words of two digits each (example : 06 12 34 56 78)
- Anniversary dates encoded into 4 concrete words (example : 24 02 1958)
- Access codes (PIN code, building door code, safe code, alarm code, etc.) encoded into 2 or 3 concrete words depending on their length
- Social security numbers encoded into an initial digit (gender : 1 male, 2 female) followed by 7 concrete words (example : 1 58 02 XX XX XX XX XX)
B4.2. Recall tables of figures from 0 to 9 :
The recall table of figures from 0 to 9 is not unique and depends on its author :
- Aimé Paris's table has the merit of codifying all common consonant sounds. The association between figure and sound(s) must be memorized.
- Joe Bertin's table associates a consonant letter with each figure, which provides a visual aid that greatly facilitates sound memorization.
- Régis Petit's table reproduces Joe Bertin's table, modifying the letters associated with the figures 2 and 4, which improves the visual aid (see Figure above).
The different tables are as follows :
Table legend : (*) according to the orthographic writing of the phonemes.
| Figure | Song (*) and image according to Aimé Paris [PAR, p.28][WIK][APP] | Other image according to Régis Petit | Song (*) and image according to Joe Bertin [BER] | Song (*) and image according to Régis Petit |
|---|---|---|---|---|
| 0 | "s" or "z", one of the loops of the letter s | SanS aide | "d", letter D | "d", letter D |
| 1 | "t" or "d", single leg of the letter t | TenDu ou Tout Droit | "t", letter T | "t", letter T |
| 2 | "n" ou "gn", double leg of the letter n | Na ! (attitude enfantine de provocation) | "n", letter N sideways | "r", letter R without a vertical bar |
| 3 | "m", triple leg of the letter n | Maman | "m", letter M sideways | "m", letter M sideways |
| 4 | "r", upside-down or mirrored letter r | trois Ratures faites avec Rage | "r", letter R mirrored | "k", letter K (with a block of three strokes) |
| 5 | "l", similar to the letter L in French cursive round writing [LIV1][LIV2] | Ligne verticale ratatinée | "s", letter S | "s", letter S |
| 6 | "ch" or "j", similar to the letter j in French cursive round writing [LIV1][LIV2] | Chat qui Jaillit | "g" ou "j", letter G | "g" ou "j", letter G |
| 7 | "k" or "g", gallows shape similar to the letter q or g | Coups Guerriers (indiqués par deux Coupures) | "l", letter L upside-down | "l", letter L upside-down |
| 8 | "f" or "v", similar to the letter F in French cursive round writing [LIV1][LIV2] | FèVe (sous forme de petit enFant) | "b", letter B | "b", letter B |
| 9 | "p" or "b", mirrored letter p or upside-down letter b | Petit Bébé (en position foetale avec sa grosse tête) | "p", letter P mirrored | "p", letter P mirrored |
B4.3. Recall tables of numbers from 00 to 99 :
Anyone can freely construct their own recall table of numbers from 00 to 99, based on a given recall table of figures.
The recall tables of numbers from 00 to 99 proposed below were created by Régis Petit. The first is based on Aimé Paris's coding of figures, the second on Régis Petit's coding of figures.
These two tables are designed according to the following rules for easy memorization of concrete words :
Concrete word = common or proper noun, with a single syllable of the CVC or CSVC type, such as :
C = consonant associated with the figure in the recall table of figures.
V = vowel that can be (*) : "é" "è" "eu" "in" "a" "an" "ou" "o" "on" "i" "u"
S = semi-consonant at the onset of a V vowel, which can be (*) : "w" "y" "u+"
The V or SV nucleus of the syllable is chosen primarily from the sounds (*) : "é" "è", "eu", "in"; "a", "an" ; "ou", "w" V ; "o", "on" ; "i", "y" V ; "u", "u+" V
(*) according to the orthographic writing of the phonemes.
Exceptions to these rules are in italics in these tables.
| Number | Concrete word conforming to Aimé Paris's coding of figures | Concrete word conforming to Régis Petit's coding of figures |
|---|---|---|
| 00 | Sas | Dinde |
| 01 | Soute | Datte |
| 02 | Scène | Dard ou Dur |
| 03 | Somme | Dame |
| 04 | Serre ou Soeur | Dock ou Duc |
| 05 | Selle | Danse |
| 06 | Souche | Danger ou Dingue |
| 07 | Sac | Dalle |
| 08 | Soif | Dab ou Daube |
| 09 | Sep | Dieppe ou Dupe |
| 10 | Tasse | Tiède |
| 11 | Tête ou Tente | Tête ou Tente |
| 12 | Tonne | Terre |
| 13 | Tome | Tome |
| 14 | Terre | Tank |
| 15 | Toile | Tasse |
| 16 | Tache | Tige ou Tag |
| 17 | Tank | Toile |
| 18 | Touffe | Tombe |
| 19 | Taupe | Taupe |
| 20 | Nasse | Rade |
| 21 | Natte | Rate |
| 22 | Nonne | Rire |
| 23 | Nem | Rame |
| 24 | Nerf | Rack |
| 25 | Nul | Race |
| 26 | Niche | Rage ou Reg |
| 27 | Nuque | Râle |
| 28 | Nef | Rab ou Robot |
| 29 | Nappe | Rampe ou Repas |
| 30 | Messe | Mode |
| 31 | Meute ou Motte | Meute ou Motte |
| 32 | Moine | Mer ou Mare |
| 33 | Môme | Môme |
| 34 | Mer ou Mare | Mec |
| 35 | Meule ou Malle | Messe |
| 36 | Mèche | Mage ou Mangue |
| 37 | Mec | Meule ou Malle |
| 38 | Moufle | Meuble |
| 39 | Myope | Myope |
| 40 | Race | Coude |
| 41 | Rate | Quinte ou Côte |
| 42 | Reine | Coeur |
| 43 | Rame | Came |
| 44 | Rire | Cake |
| 45 | Râle | Caisse |
| 46 | Roche | Cage |
| 47 | Rack | Cale |
| 48 | Rouf ou Rêve | Cube |
| 49 | Râpe | Coupe ou Cape |
| 50 | Laisse | Soude |
| 51 | Latte | Soute |
| 52 | Laine | Serre ou Soeur |
| 53 | Lame | Somme |
| 54 | Lard | Sac |
| 55 | Lille | Sas |
| 56 | Louche | Singe ou Sangle |
| 57 | Lac | Sel |
| 58 | Lymphe | Sabre |
| 59 | Loupe | Soupe |
| 60 | Chasse | Jade ou Guide |
| 61 | Jante ou Chatte | Jatte ou Goutte |
| 62 | Jeune ou Chaîne | Jour ou Gare |
| 63 | Gym ou Chaume | Gym ou Gamme |
| 64 | Jour ou Chair | Jonque |
| 65 | Gel ou Châle | Gousse |
| 66 | Juge | Juge ou Gong |
| 67 | Jonque ou Chèque | Gel ou Gueule |
| 68 | Chef | Jambe |
| 69 | Jupe ou Chappe | Jupe ou Guêpe |
| 70 | Caisse | Lad ou Lande |
| 71 | Quinte ou Côte | Latte |
| 72 | Canne | Lard |
| 73 | Came | Lame |
| 74 | Coeur | Lac |
| 75 | Cale | Laisse |
| 76 | Couche | Linge ou Langue |
| 77 | Cake | Lille |
| 78 | Coiffe | Lobe |
| 79 | Coupe ou Cape | Lampe |
| 80 | Fesse | Bande |
| 81 | Fête | Bête |
| 82 | Fouine | Beurre |
| 83 | Femme | Boum |
| 84 | Fer | Banque |
| 85 | Foule ou Fil | Bosse |
| 86 | Fiche ou Vache | Bouge ou Bague |
| 87 | Fac | Balle |
| 88 | Fief | Bob |
| 89 | Vamp | Bip |
| 90 | Pince | Panda ou Poudre |
| 91 | Patte | Patte |
| 92 | Panne | Poire |
| 93 | Pomme | Pomme |
| 94 | Père | Pack ou Pique |
| 95 | Pelle | Panse |
| 96 | Pêche | Page |
| 97 | Pack ou Pique | Pelle |
| 98 | Pouf | Pub ou Poubelle |
| 99 | Pape ou Poubelle | Pape |
B4.4. Sources :
[APP] Apprendre5minutes, Comment mémoriser facilement les chiffres ou les nombres
[BER] Joe Bertin, Astuce de mémorisation : la table de rappel
[LIV1] French Handwriting Schoolbook, écriture ronde française
[LIV2] pilllpat (agence eureka), album Alphabete
[PAR] Aimé Paris, Exposition et pratique des procédés mnémotechniques à l'usage des personnes qui veulent étudier la mnémotechnie en général comme un moyen d'abréger l'étude de toutes les connaissances humaines, Paris, 1825
[WIK] Wikipedia, Code chiffres-sons
B5.1. Introduction :
A palindrome is a form of linguistic symmetry where a sentence (which can be as short as a single word) reads or sounds the same in both directions. See Attributed palindromic sentences, Anonymous palindromic sentences, Palindrome cities and Palindrome first names.
Orthographic palindromes are based on the order of letters in writing, as in "C'est sec".
The same applies to word palindromes that are based on the order of words in writing, as in "Un pour tous, tous pour un" or in "La juste est juste là" (for a non-strict palindrome).
The same applies to syllabic palindromes at the syllable pronunciation level, as in "Laconique Nicolas", corresponding to the syllabic sequence "la" "ko" "ni" "ke" "ni" "ko" "la".
The same applies to phonetic palindromes at the phoneme pronunciation level, as in "Il aima Amélie", corresponding to the phonetic sequence "i" "l" "é" "m" "a" "a" "m" "é" "l" "i".
The same applies to numeric palindromes at the writing level, as in the date "02/02/2020".
The same applies to Rotational palindromes at the writing level, as the word "inoui".
The same applies to mirror palindromes which read identically after reflection in a mirror.
The same applies to musical palindromes at the level of the notes of the musical phrase.
The palindromes listed below are exclusively orthographic palindromes in the French language, where case (upper/lower case), diacritical marks (accent, diaeresis, cedilla, tilde, etc.), spaces and punctuation marks (period, comma, dash, parentheses, etc.) are not taken into account.
B5.2. Attributed palindromic sentences :
The most beautiful palindromic sentences in the French language, attributed to an author, are the following :
A Cuba, Anna a bu ça (Gérard Durand).
A Laval, elle l'avala (Michel Laclos).
A l'étape, épate-la ! (Louise de Vilmorin).
A révéler mon nom, mon nom relèvera (Edmond Rostand, dans Cyrano de Bergerac).
Ce satrape repart à sec (Pierre Bailly).
C'est sec (Roger Cornaille).
Eh ! ça va la vache ? (Louise de Vilmorin).
Elisa, là, à l'asile (Lennig Gullon).
Elu par cette crapule (Charles Cros).
Emile-Eric, notre valet, alla te laver ton ciré élimé (Georges Perec).
Engage le jeu que je le gagne (Alain Damasio).
En nos repères, n'insère personne (Dominic Bergeron).
En route je tourne (Roger Cornaille).
Eric, notre valet, alla te laver ton ciré (Jacques Capelovici).
Esope reste ici et se repose (Jacques Capelovici).
Etel, un port trop nu, l'été (Claude Gaignière).
Et la Marine va venir à Malte (attribué à Victor Hugo).
Et Luc colporte trop l'occulte (Michel Laclos).
Karine égarée rage en Irak (Gérard Durand).
Karine libre à Erbil en Irak (Christophe L.)
La Marine en ira mal (attribué à Victor Hugo).
La mariée ira mal (Louise de Vilmorin).
L'âme des uns n'use de mal (Etienne Pasquier).
L'amer vin enivre mal (Jean T.).
La mère Gide digère mal (Louis Scutenaire).
L'âme sûre ruse mal (Louise de Vilmorin).
L'ami naturel ? Le rut animal ! (Louise de Vilmorin).
Lune de ma dame d'été, été de ma dame de nul (Louise de Vilmorin).
Nier est effet serein (Stéphane Susana).
Noël a trop par rapport à Léon (Sylvain Viart).
Oh ! cet écho (André Tomkins).
Par-delà le drap (Patrick Hospital).
Rions noir (Jacques Bens).
Rue Verlaine gela le génial rêveur (Jacques Perry-Salkow).
Ta bête te bat (Louise de Vilmorin).
Un art luxueux ultra nu ! (Matthieu Godbout).
Un émir fada, venu du Nevada, frime nu (Gérard Durand).
B5.3. Anonymous palindromic sentences :
The most beautiful palindromic sentences in the French language, without a known author, are the following :
A l'autel elle alla, elle le tua là.
Bon sport, trop snob.
Car, tel Ali, il a le trac.
Ce mec.
essayasse.
Etna : lave dévalante.
Etre là, alerte.
Et se resservir, ivresse reste.
Et Tesio, né borné et naïf, emporte une vedette devenue trop méfiante en robe noisette (Francis Pacherie).
Ici.
Il a pâli.
Il a sali.
Karine alla en Irak.
L'âge légal.
La malade pédala mal.
L'âme d'Eve rêve de mal.
La mère puce récupère mal.
L'âne vénal.
malayalam (langue parlée en Inde).
mon nom.
Nie, reste net, serein.
Ni lac, ni patelin, ni le tapin câlin.
Oh ! Cela te perd, répéta l'écho.
ressasser.
Réussir à Paris : suer.
rotavator.
S'engager à revers : rêver à regagnes !
Sexe vêtu, tu te vexes ?
Ta belle porte s'use trop, elle bat.
Trace là mon nom à l'écart.
Un drôle de lord nu.
Un ému a son os au menu.
Un enfer bref. Né nu.
Un été nu.
Un rêve de ver nu.
Un roc lamina l'animal cornu.
Un roc si biscornu.
Zeus a été à Suez.
B5.4. Palindrome cities :
The main palindrome cities of the world are the following :
Allemagne : Burggrub (Bavière), Hammah (Basse-Saxe), Mussum (Rhénanie-du-Nord-Westphalie), Woddow (Brandenburg), Zeez (Mecklenburg-Vorpommern)
Angola : Seles (Cuanza Sul)
Arabie Séoudite : Al'Ula (Madinah)
Argentine : Neuquén (Patagonie)
Australie : Aramara (Queensland), Arrawarra (Nouvelle-Galles-du-Sud), Civic (Territoire de la Capitale Australienne), Glenelg (Adélaïde, Australie-Méridionale), Hattah (Victoria), Lal Lal (Victoria), Parap (Territoire du Nord), Paraparap (Victoria), Tumut (Nouvelle-Galles-du-Sud)
Belgique : Eke, Ellemelle (Province de Liège), Ere
Brésil : Aba (Bahia), Acaiaca (Minas Gerais), Aia (Ceara), Mutum (Minas Gerais)
Burkina Faso : Bob (Région du Centre-Ouest)
Canada : Elôle (Québec), Kinikinik (Alberta), Laval (Québec), Navan (Ontario), Salas (Nouvelle-Ecosse), Wakaw (Saskatchewan)
Chili : Lolol (O'Higgins)
Chine : Nan'an (Fujian)
Danemark : Dragsgard, Vellev
Egypte : Aga (gouvernement de Daqahliyya)
Espagne : Aba (Pays basque), Aja, Aya, Oco, Ollo (Navarre), Oro, Oso (Catalogne), Salas (Asturie), Saras, Senés (Andalousie), Sotos
Etats-Unis : Ada (Oklahoma, Oho, Minnesota), Ala (Alabama), Anna (Ohio, Texas, Illinois), Ava (Missouri, Illinois, New York), Capac (Michigan), Civic (Canberra), Eleele (Hawaï), Hannah (Michigan, Dakota du Sud, Caroline du Nord), Harrak (Oklahoma, Washington), Ixixi (Alaska), Kanakanak (Alaska), Kinikinik (Colorado), Level (Ohio, Maryland), Noxon (Montana), Otto (plusieurs Etats), Oto (Iowa), Remer (Minnesota), Renner (Texas), Wassamassaw (nom d'une région de Caroline du Sud)
Ethiopie : Asasa, Asosa
Finlande : Asa (Laponie), Esse, Ii (Ostrobotnie), Orö
France : Afa, Callac, Esse, Eve, Eze, Laval, Noron, Noyon, Oô, Sajas, Sanas, Saras, Savas, Sées, Selles, Senones, Serres, Sos, Sus
Grèce : Sedes, Serres
Groenland : Qaanaaq (Région Qaasuitsup)
Hongrie : Tat, Tét, Pap, Ziliz
Inde : Ara (Bihar), Aramara, Atta (Uttar Pradesh), Aya (Maharashtra), Gadag (Karnataka), Idappadi (Tamil Nadu), Itamati (Odisha), Rapar (Gujarat), Nawagawan
Iran : Barab, Basab, Kahak, Karak, Kuruk, Naran, Qoroq, Sarras, Selles, Sis, Sus, Tabbat
Irlande : Navan (Comté de Meath)
Israël : Akka, Na'an
Italie : Ala (Trentin-Haut-Adige), Ateleta (Abruzzo), Erre (Podesteria, ancien nom), Onano (Latium), Onno (Lombardie), Sennes (Tyrol du Sud), Siris (Calabre)
Japon : Aka (Fukuoka), Akasaka (Tokyo, Okayama), Ama (Shimane), Awa (Tokushima), Ono (Préfecture de Hyogo)
Mali : Tamahamat, Tassassat
Maroc : Akka, Assa
Mauritanie : Tétêt (Région de l'Adrar)
Niger : Tabadabat, Tassessat
Nigeria : Aba (Etat d'Abia), Abiriba, Apapa, Elele (Rivers), Irri, Ososo, Oyo (Etat d'Oyo)
Nouvelle-Zélande : Aka Aka (Auckland)
Pays-Bas : Ede (Province de Gueldre), Ee (Province de Groningue), Epe (Province de Gueldre)
Pologne : Wolow (Basse-Silésie)
République tchèque : Vokov
Roumanie : Anina (Judet de Caras-Severin)
Royaume-Uni : Anna (Suffolk), Eve (Ecosse), Eye (Cambridgeshire, Suffolk), Glenelg (Ecosse), Notton (West Yorkshire, Angleterre)
Russie : Aga (République de Sakha) Tommot (Iakoutie), Ulu (Iakoutie), Yessey (Krasnoïarsk)
Sénégal : Matam (Région de Matam)
Suède : Abba (Province de Dalécarlie), Dörröd, Kivik, Murum
Suisse : Planalp (Obwald)
Thaïlande : Nan (Province de Nan)
B5.5. Palindrome first names :
The main palindrome first names are the following :
Legend : (*) indicates the most common palindrome first names in France (born in France or listed in the INSEE "First Names" database since 1900).
Female first names :
Ada (*), Adda
Aa
Anevena
Anina
Anona
Arezera
Afifa
Aviva
Aia, Aya
Arora
Atta
Ece
Elle (*)
Eve (*)
Hawah, Hawwah
Immi
Ireri
Ivi
Izzi
Layal
Lenel
Malayalam
Maram
Okko
Viv
Male first names :
Aba, Abba
Alla
Aoloa
Bob (*)
Did
Efe
Lehel
Nan
Natan (*), Nattan
Nayan
Neven
Odo
Oto, Otto (*)
Reber
Reinier
Sabas
Savas
Talat, Tanat
Unisex first names :
Aja (*)
Ama (*), Amma
Ana (*), Anna (*), Anena, Hannah (*)
Ara
Asa
Ava (*), Awa
Axa
Aza, Azza, Aziza
Civic
Ebbe
Ede
Eme, Emme (*)
Görög
Kajak, Kayak
Lil (*), Lyl
Noon
Nosson
Ono
Siris
Uru
Yay
Zaz
B5.6. Word palindromes :
Word palindromes are phrases that read identically from right to left and from left to right at the word level, regardless of case (upper/lower case) and punctuation marks (period, comma, dash, parentheses, etc.), as in the following examples :
Un pour tous, tous pour un
Papa aime maman, maman aime papa
Nous avions les avions, nous !
Pierre baise à Baise-Pierre
Some word palindromes, less strict, allow the omission of diacritical marks (accent, diaeresis, cedilla, tilde, etc.), as in the following examples :
La juste est juste là
La foule, foule-là !
Saint-Pierre a marié Marie à Pierre Saint
B5.7. Numeric palindromes :
The major numeric palindrome are the following [PAL][VIL] :
02-02-2020
21-12-2112
121 = 38 + 83 = 121
12 345 678 987 654 321 which is the square of palindromic number 111 111 111
982 623 644 294 744 275 088 611 239 676 071 787 170 676 932 116 880 572 447 492 446 326 289 which is the square of non-palindromic number 31 346 828 297 209 660 045 268 842 120 992 233 (July 5, 2024 - Patrick De Geest)
1 030 607 060 301 which is the cube of palindromic number 10 101
1 331 000 039 930 000 399 300 001 331 which is the cube of palindromic number 1 100 000 011
10 662 526 601 which is the cube of non-palindromic number 2 201
B5.8. Rotational palindromes :
Rotational palindromes (also called "rotational ambigrams") are words or phrases that read identically after rotating the entire set halfway.
This property applies exclusively to the following characters [AMB][DEL] :
Digits : 0, 1, 8, which remain invariant under rotation, and 6/9 which are rotation pairs of each other.
Punctuation marks : - : () [] {} which remain invariant under rotation.
Symbols : + - / x = ≠ ∞ \ ∫ ⊗ # $ % § | θ ι ο χ which remain invariant under rotation.
Capital letters : H, I, N, O, S, X, Z, which remain invariant under rotation, and M/W which are rotation pairs of each other.
Lowercase letters : i, l, o, s, x, z, which remain invariant under rotation, and a/e, b/q, d/p, h/y, m/w, n/u, which are rotation pairs of each other.
The most beautiful rotational palindromes are the following :
NON
SOS
SONOS
NOW NO SWIMS ON MON (qui signifie "Maintenant plus de piscine le lundi")
NeW MaN
aie
axe
aune
yeah
apode
inoui
sales
saxes
suons
nounou
salles
saisies
saillies
elle alla
andin basnoda a une épouse qui pue (Georges Perec).
Note that some words can give rise to another word by rotating it halfway. Examples :
91 = 90 + 01 / 10 + 06 = 19
NOM/WON
NOS/SON
las/sel
epis/sida
eues/sana
iles/sali
oued/pano
sans/sues
ailes/salie
aillé/allié
esses/sassa
assassins/suissesse
le pou / nodal
Also note that some words can give rise to the same word or another word by rotating them a quarter turn. Examples :
Counterclockwise (where the capital letters C E H I M N O X Z become respectively U W I H E Z O X N) :
OHIO/OHIO
MON/ZOE
ZOE/WON
con/cou
Clockwise (where the capital letters E H I N O U W X Z become respectively M I H Z O C E X N) :
OIE/OHM
ZOE/NOM
B5.9. Mirror palindromes :
Mirror palindromes are words or phrases that exhibit axial symmetry, either horizontally or vertically, and read identically when viewed in a mirror held horizontally or vertically.
Horizontal symmetry reverses top and bottom, while preserving left and right and the order of the letters. BEC in a horizontal mirror remains BEC.
Vertical symmetry reverses left and right as well as the order of the letters within the word, while preserving top and bottom. TOUT in a vertical mirror becomes TUOT.
These symmetry properties applie exclusively to the following characters [AMB][DEL] :
Horizontal symmetry :
Numbers : 0, 1, 3, 8
Punctuation marks : . - : () [] {}
Symbols : + - x = > < ∑ ∞ ∫ ⊗ | € ε θ ι κ ο χ
Uppercase letters : B, C, D, E, H, I, K, O, X
Lowercase letters : c, i, k, l, o, x
Vertical symmetry :
Numbers : 0, 1, 8
Punctuation marks : . - : " '
Symboles : + - ± x = * ∏ ∞ ⊗ ° _ | γ θ ι ν ο π τ υ χ ψ ω
Uppercase letters : A, H, I, M, O, T, U, V, W, X, Y
Lowercase letters : i, l, m, o, u, v, w, x
Examples of mirror palindromes with horizontal symmetry :
BEC
BICHE
DIODE
EXCEDEE
kilo
Examples of mirror palindromes with vertical symmetry :
TOT
AVIVA (3ème personne du singulier du passé simple du subjonctif du verbe aviver
MAOAM (marque de bonbons pâte à mâcher d'origine allemande)
MATAM (ville du Sénégal)
TAMAT (3ème personne du singulier de l'imparfait du subjonctif du verbe tamer)
TATAT (3ème personne du singulier de l'imparfait du subjonctif du verbe tâter)
TAXAT (3ème personne du singulier de l'imparfait du subjonctif du verbe taxer)
HAITI, AH !
MOT A TOM
wow (interjection d'origine anglaise exprimant la surprise ou l'émerveillement)
B5.10. Musical palindromes :

Musical palindromes are sound sequences constructed to remain identical when played in either direction, according to two possible types of symmetry :
- Retrograde (B), which consists of replaying the sequence of notes (A) in reverse order in time. Example (see Figure above) : The original sequence Do Ré Mi Fa Sol La Si La Sol Fa generates the inverse sequence Fa Sol La Si La Sol Fa Mi Ré Do.
- Inversion (C), which consists of replaying the sequence of notes by reversing the direction of the intervals between these notes around an imaginary horizontal axis. Example (see Figure above, with Do chosen as the reference point for the horizontal axis) : The sequence Do Ré Mi Fa Sol La Si La Sol Fa generates the inverse sequence Do Sib Lab Sol Fa Mib Réb Mib Fa Sol.
- The retrograde of inversion (D), which consists of combining these two processes. Example (see Figure above) : The combination of the two previous examples generates the sequence Sol Fa Mib Réb Mib Fa Sol Lab Sib Do.
Warning : Palindromic inversion (C) is different from inversion of an interval or chord in music.
Depending on the composer, pieces A, B, C and D can be mixed in sequence or superimposed. For example :
In Guillaume de Michaut ("My End Is My Beginning") : Superimpose A + B + C', where the Tenor voice is an integral part of A.
In J.S. Bach (Musical Offering, Canon Cancrizans, or Canon Per Motum Contrarium) : Superimpose A + B or sometimes superimpose A + D
In Haydn (Symphony No. 47, Minuet of the Palindrome) : Sequence A then B then C then superimpose A + D
B5.11. Sources :
[AMB] Wikipedia - Ambigramme
[DEL] Jean-Paul Delahaye, Ambigrammes, revue Pour la Science, N° 323, Septembre 2004
[DUR] Gérard Durand, Palindromes en folie
[PAL] The Palindrome, Palindrome ?
[QUI] Quillbot, Palindromes
[RED] reddit, Quelle est la plus grande ville du monde qui porte un nom palindromique ?
[STA] StarinuX, Liste de palindromes
[VIL] Gérard Villemain, Langue - Palindromes - Villes
[VIL] Gérard Villemain, Formes- Palindromes - Introduction
[VIL] Gérard Villemain, Formes - Palindromes - Dates
[VIL] Gérard Villemain, Formes- Palindromes - Carrés
[VIL] Gérard Villemain, Formes- Palindromes - Cubes
[WIK] Wikipedia, Palindrome
[WIK] Wikipedia, Liste des palindromes en français
[WIK] Wikipedia, Palindrome (multilangues)
Contents :
B6.1. Magic tricks with ropes or rubber bands :
Here are some spectacular tricks using ropes, rubber bands or just your hands.
B6.1.1. Hands turned over :
This trick is a popular cognitive psychology experiment.
A spectator is asked to interlace their fingers, palm to palm, in an inverted position, and then turn them over.
This slightly uncomfortable position exposes both rows of fingers to the upwards (see Figure above).
A specific finger is then pointed out without being touched, and the spectator is asked to raise it quickly and without thinking.
The spectator then frequently raises the opposite, symmetrical finger.
This error arises from a conflict between an internal representation of the fingers, disrupted by the unusual posture, and the automatic motor commands, designed for hands in a normal position. Vision could correct this, but not quickly enough when an immediate response is required.
B6.1.2. Battery swap between two hands :

This dexterity trick involves swapping two round AA batteries from one hand to the other without dropping them or using any special effects.
The manipulation is simple and quick, but difficult for a spectator to reproduce.
The steps are as follows (see Figure above, cf. [PRA][ASH]) :
1. Hold a round AA battery in the crook of each thumb and index finger, pinching the battery in the middle, slightly angled towards the wrist, with the bottom (negative pole) facing the palm.
2. Position your hands facing the spectator, palms hidden, in head-to-tail position, with your fingers horizontal and in a vertical plane.
3. Rotate your right hand a quarter turn counterclockwise.
4. Bring your hands together, keeping your fingers parallel, with your right thumb sliding under your left thumb.
5. Place each thumb on the bottom of each battery and loop each miidle finger over the other end of the batteries (positive pole).
6. Pinch each battery between your thumb and middle finger, then gently separate your hands.
7. Rotate both hands slightly to present the two batteries vertically to the spectator.
8. Return the batteries to their initial position (step 1) by reversing the steps.
Note : Instead of pinching the batteries between thumb and middle finger, you can also do it between thumb and index finger (as shown in the Figure above), but this finger position during the cross-locking (step 5) is more forced and less comfortable.
B6.1.3. The traveling ring :

1. This spectacular trick requires a ring and a cut not-too-bright rubber band approximately 10 cm long (see Figure above, cf. [MIR]).
2. Coil the rubber band in your left hand, leaving about 1 cm of the end sticking out. Pinch the end firmly between your thumb and index finger, then pass the rubber band through the ring.
3. Grasp the rubber band between the thumb and index finger of your right hand, tender it to the maximum, and tilt it slightly upwards. The ring will naturally stop against your left hand.
4. Without moving either hand, the ring will then begin to slowly slide up the rubber band.
Solution : After stretching the rubber band, let it slide gently between the thumb and index finger of your left hand, causing the ring to slide up.
B6.1.4. Bouncy rubber band between fingers :
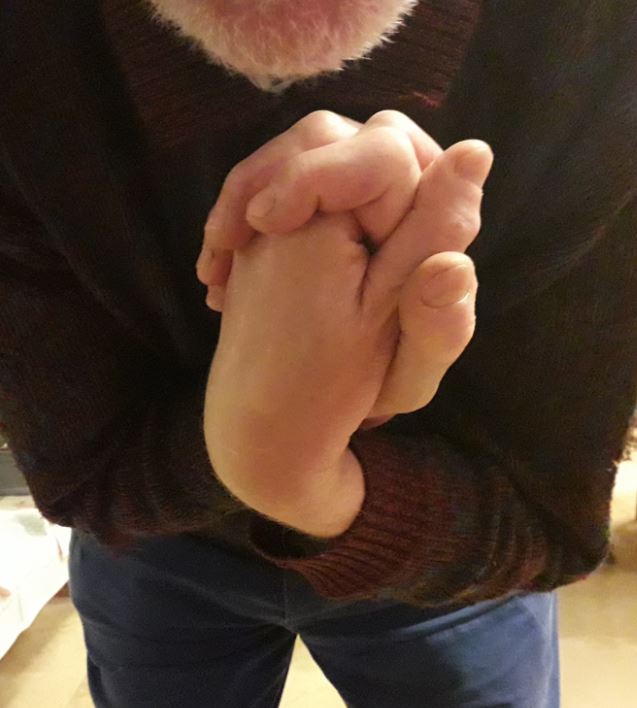
This magic trick requires a small, brightly colored rubber band.
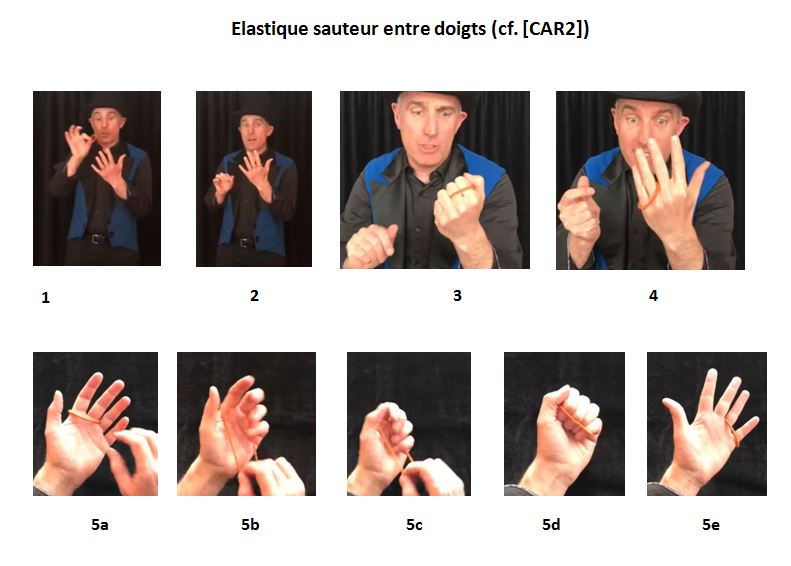
The steps are as follows (see Figure above, cf. [CAR2]) :
1. Facing the spectator, hold the rubber band above a vertical hand.
2. Loop the rubber band around the index and middle fingers of this hand.
3. Press your fingers and thumb against the rubber band and close your fist, saying this aloud.
4. Blow on your fingers and reopen your fist. The rubber band will suddenly jump and wrap around the other two fingers.
Explanation : Just before closing your fist, grasp the rubber band between the thumb and index finger of your other hand (5a), pull it quickly down to the base of your palm (5b), close your fist (5c), and place the rubber band at the base of your four fingernails, starting with your little finger and working towards your index finger (5d). Then open your fist (5e).
Improved solution : To better conceal this secret manipulation, before closing the fist, grasp the rubber band, pull it back with your index finger while pressing your palm against your wrist, thumb and other fingers facing the spectator, close your fist, lower your arms under the table, place the rubber band on your fingers, re-press the wrist, and show the whole thing unchanged to the spectator. Then open your fist.
B6.1.5. Bouncy rubber band between hands :
This magic trick requires two rubber bands of the same color and quite long.
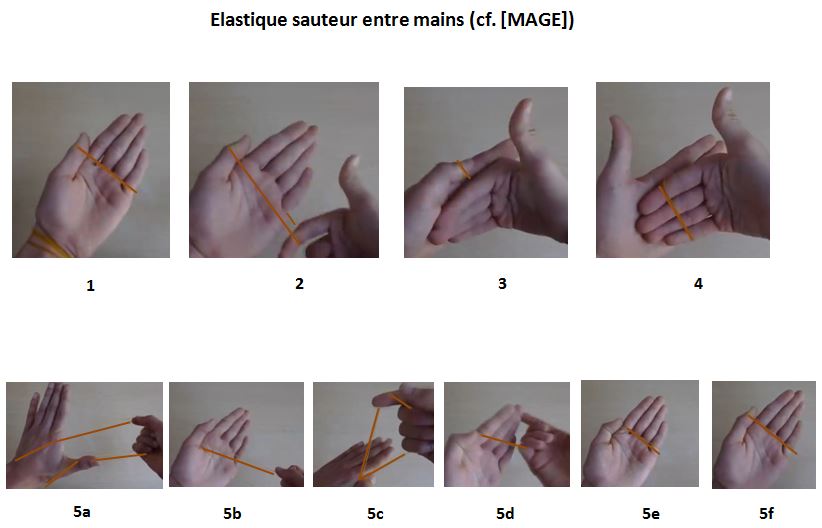
The steps are as follows (see Figure above, cf. [MAGE]) :
1. Present your open palm to the spectator, with a rubber band around the top of your thumb and the base of your other four fingers.
2. Using the index finger of your other hand, gently peel the rubber band away from your palm to clearly demonstrate that it is normal.
3. Present your other hand upside down and tap your fingers together.
4. Raise your thumb. The rubber band will suddenly jump onto the four fingers of your other hand.
Solution : Prepare the rubber band as follows :
5a. Place the rubber band around your wrist, on the palm side, then in the hollow between your thumb and your index finger.
5b. Press your thumb firmly against your index finger to secure the rubber band, then turn your hand over so your palm is facing up.
5c. Pass the rubber band between the top of your thumb and index finger, maintaining pressure.
5d. Turn your hand over so your palm is facing down, then pass the loop of the rubber band around your four fingers.
5e. Turn your hand over again, palm up, with the rubber band positioned at the base of your four fingers.
5f. Pull the rubber band slightly to pass it over the top of your thumb.
5g. Place a second rubber band around your wrist to conceal the secret preparation.
The preparation is now complete, and the trick can begin in front of a spectator.
B6.1.6. Intertwined rubber bands :

This magic trick requires two small, identical rubber bands of the same color.
The steps are as follows (see Figure above, cf. [JER]) :
1. Hold one rubber band vertically between the thumb and forefinger of your left hand, and another between the thumb and middle finger of your right hand, with the two rubber bands intertwined.
2. Move both hands by bringing them together and moving them apart, and also by rotating them in opposite directions, to show the spectator that the system is locked.
3. Suddenly separate your hands. Both rubber bands will be released.
Solution :
4a. As you rotate your hands, pass your right index finger, which is free, through the loop of your right thumb.
4b. Push your right index finger in and pass it behind the left rubber band.
4c. Remove your right middle finger from the right rubber band.
4d. The rubber band will automatically move over your right index finger.
4e. Immediately press the rubber band against the other one to simulate the lock.
4f. Suddenly move your hands apart.
Improved solution (cf. [PAU][VAL]) :
In step 1, hold the rubber band horizontally (and not vertically), which avoids passing behind the left rubber band in step 4b.
B6.1.7. String handcuffs puzzle :

This spectacular trick is the following :
1. Two people are standing facing each other (see Figure above, cf. [EIT]).
Each person's wrists are connected by a rope approximately 1 meter long, forming a loose loop around each wrist and secured with a knot that is assumed to be unbreakable.
The two ropes are intertwined, thus connecting the two people.
How can they separate without cutting the rope, without untying the knots, and without the rope slipping down their hands ?
Solution :
2. Make a Bight (loop in the shape of an elongated U) with your own rope behind your partner's rope.
3. Pass the Bight through the loop around your partner's wrist, from the arm towards the fingers.
4. Pass the Bight over your partner's hand.
5. Pull on the rope : it miraculously comes undone, and the two people are then completely separated.
B6.1.8. Escape with bound hands :
This magic trick requires only a rope approximately 70 cm long.
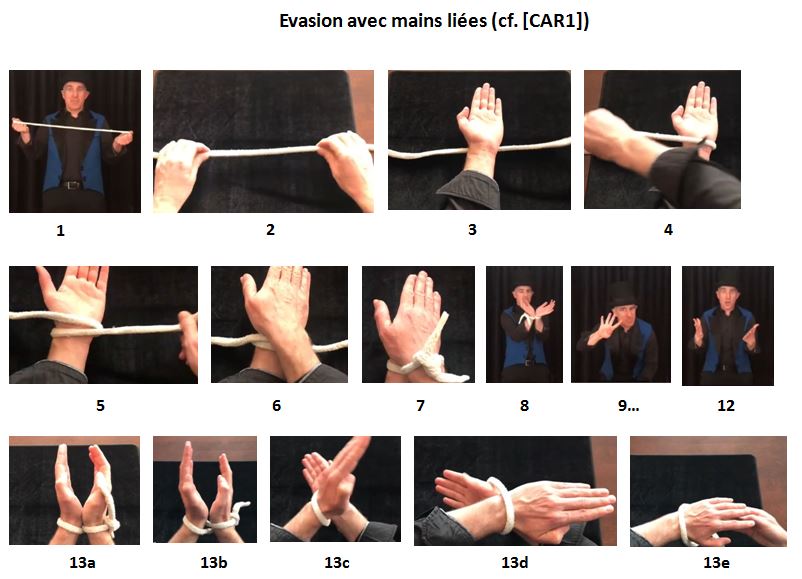
The steps are as follows (see Figure above, cf. [CAR1]) :
1. Place a table between you and the spectator and show a "very strong rope" stretched taut between your two hands.
2. Lay the rope on the table, parallel to the spectator.
3. Place your left hand in the middle of the rope, palm facing up.
4. Bring the right end of the rope over your left wrist, and in front of the left end.
5. Bring the left end of the rope over your right wrist, without crossing the other end.
6. Place your right hand on top of your left hand, palm facing down.
7. Ask the spectator to take the two free ends and tie them together above your hands with three tight knots.
8. Raise your arms, showing your hands tied together.
9. Lower your hands behind the table and then immediatly... raise your free right hand.
10. Lower your free hand behind the table and then immediatly... raise both hands again.
11. Repeat steps 9 to 10.
12. Lower your hands behind the table and then immediatly... raise both hands.
Explanation : Behind the table, rotate each wrist a quarter turn in the opposite direction (13a, 13b, 13C, 13d) and take the right hand out of the loop (13e). Reverse the movement to reattach both hands.
Note : a more sophisticated version of this trick exists (see [HAF]).
B6.2. Magic tricks with playing cards :
Here are some spectacular card tricks that can be done by children.
B6.2.1. The thieving Jacks :

This trick requires a 32-card deck :
1. Take three Jacks from a deck of cards and leave the deck face down on the table.
2. Tell the story : "Three thieves want to break into a house...
3. The first finds a basement window and goes through the cellar (place a Jack under the deck).
4. The second climbs onto the roof and goes through the attic (place a Jack on top of the deck).
5. The third finds an open window and goes down to the ground floor (insert a Jack into the deck)."
6. Ask the spectator to "cut" the deck.
7. Announce that the three Jacks will be together and fan out the deck to verify this.
Solution : Prepare the deck by placing a Jack (the fourth) on top. The three Jacks reunited at the trick end are not the same, but this often escapes the spectator.
B6.2.2. The four Kings :

This trick is a variant of the "Three thieves" trick. It requires a 32-card deck :
1. Fan out the four Kings in front of the spectator.
2. Stack them on top of the remaining deck.
3. Take the four top cards one by one and insert them into the deck.
4. Ask the spectator to "cut" the deck into two approximately equal parts.
5. Announce that the four Kings will be together and fan out the deck to verify this.
Solution : Before starting the trick, discreetly add a stack of four more cards under the fan of the four Kings, well hidden by the first King (see Figure above).
B6.2.3. The four Aces :

This trick requires a 32-card deck :
1. Give the spectator a deck of cards to shuffle, then take the deck back, and present it vertically, facing the spectator.
2. Ask him to take one of the Aces and place it face down against his chest.
3. Pass the deck behind your back, then show it to the spectator again, asking him to replace his Ace in the deck.
4. Give the deck back to the spectator to shuffle, then take the deck back, and remove the chosen Ace.
Solution :
- Prepare the deck by setting the "point" of each Ace in the card center in the same orientation (spades, hearts, clubs), the Ace of diamonds being symmetrical (see Figure above).
- Behind your back, turn the deck of cards halfway around (top/bottom reversed).
- The chosen Ace is the Ace of diamonds if no "point" is reversed, and the Ace with a reversed "point" otherwise.
- Warning : Remove the chosen Ace from the deck, thumb pointing towards you, then present the card to the spectator, thumb pointing towards him (this reverses the card's orientation so the trick can be repeated). Then place the card back in the deck, thumb pointing towards the spectator.
Note : In terms of face cards (Jack, Queen, King, and Joker), numbered cards (from Ace to Ten), and possible indexes placed in opposite corners, standard post-19th-century French 54-card decks generally feature cards that are symmetrical by rotating them a half turn. There are 18 exceptions : the two Jokers (red and black), the four Sevens (one for each suit), and four triplets of cards (spades, hearts, clubs) corresponding to Aces, Threes, Fives, and Nines.
B6.2.4. The found card : :

This trick is a spectacular and little-known generalization of the "Four Aces" trick. It requires a 32-card deck :
1. Give the spectator a deck of cards to shuffle, then take the deck back, and present it vertically, facing the spectator.
2. Ask him to take any card and place it face down against his chest.
3. Pass the deck behind your back, then present it to the spectator again, asking him to replace his card in the deck.
4. Give the deck back to the spectator to shuffle, then take the deck back, present it fanned out, quickly scroll through the cards one by one, and remove the chosen card.
Solution :
- Not every deck of cards has perfect printing in the center of each card. The white band separating the top edge of the card from the top of its printed portion (the short side of the rectangle surrounding each face card, or the head of each number) is not identical at the top and bottom of the card. With few exceptions, each card therefore has a small band and a large band.
- Prepare the deck by setting the small band on the same side throughout. If the band is almost identical at the top and bottom of the card, discard the card from the deck.
- Behin your back, turn the deck of cards halfway around (top/bottom reversed).
- When scrolling through the cards, aim for the top band. The chosen card is the one whose band suddenly changes size (small/large) due to a stroboscopic effect.
- Warning : Remove the chosen card from the deck, thumb pointing towards you, then present the card to the spectator, thumb pointing towards him (this reverses the card's orientation so the trick can be repeated). Then place the card back in the deck, thumb pointing towards the spectator.
B6.2.5. Magical memorization :

This spectacular trick requires a 32-card deck :
1. Shuffle the deck.
2. Pass the deck behind your back, move the bottom card to the top, and present the deck vertically, facing the spectator.
3. Announce the card and repeat from step 2.
4. Continue in this way with all the cards in the deck.
Solution :
- At the end of the shuffle, discreetly memorize the last card on the bottom of the deck.
- While presenting the deck to the spectator, memorize the bottom card that is facing you.
B6.2.6. The 27-card trick :

This purely mathematical trick requires a 32-card deck :
1. Make a deck of exactly 27 cards.
2. Fan out the deck to the spectator. Ask him to mentally remember a card C and then to give a number N from 1 to 27. Secretly calculate the number R = N - multiples of 9, adjusting R between 1 and 9 (examples : if N = 18, then R = 9 ; if N = 22, then R = 4).
3. Turn the deck face down and arrange the cards face up on the table in three columns of nine cards each, placing them in horizontal rows of three, from left to right and from top to bottom (see Figure above).
4. Ask the spectator to point to the column containing his card, then stack the cards, face up and column by column, picking up the designated column in the position p = R - multiples of 3, adjusting p between 1 and 3 (example: if R = 4, then p = 1). More simply, column p is immediately visible without any calculation by distributing R in a 3x3 square, in horizontal rows of 3, from left to right and from top to bottom (see Figure above).
5. Turn the deck face down again and form three columns of nine cards each again, as before, and ask for the column again. Stack the cards, face up and column by column, picking up the designated column in position q = 1 + Int[(R - 1)/3] (example : if R = 4, then q = 2). More simply, column q is immediately visible without any calculation by distributing R in a 3x3 square, in vertical columns of 3, from top to bottom and from left to right (see Figure above).
6. Turn the deck face down again and form three columns of nine cards each again, as before, and ask for the column again. Locate card C in position R of this column. Stack the cards, face up and column by column, picking up the designated column in position r = 1 + Int[(N - 1)/9] (example : if N = 22, then r = 3). More simply, column r is immediately visible without any calculation by distributing N in a 9x3 rectangle, in vertical columns of 9, from top to bottom and from left to right (see Figure above).
7. Turn the deck face down and place the cards one by one face down on the table, counting from 1. On the Nth card, announce card C and turn it face up.
Demonstration :
Let p, q and r be the order numbers (between 1 and 3) in which the designated column is picked up at each spread of the cards in three columns.
Let Np, Nq and Nr be the position in the deck (between 1 and 27) of the first card in the block containing card C, after picking up the designated column p, q or r, and reforming the deck.
At each spread, the exact position of card C in the deck is not determined, but rather the position of the first card in the block containing it. The size of this block is divided by 3 at each step.
At the first spread, the deck of 27 cards is divided into 3. After picking up column p and reforming the deck, card C is mechanically located in a continuous block of 9 cards, the position of the first card of which is :
Np = 1 + 9(p - 1), corresponding to the interval Ip = [Np, Np + 8].
Examples :
If p = 1, Ip = [1, 9].
If p = 2, Ip = [10, 18].
If p = 3, Ip = [19, 27].
At the second spread, this block of 9 cards is divided into 3. After picking up column q and reforming the deck, card C is mechanically located in a continuous block of 3 cards, the position of the first card of which is :
Nq = 9(q - 1) + 1 + (Np - 1)/3 = 1 + 9(q - 1) + 3(p - 1), corresponding to the interval Iq = [Nq, Nq + 2].
Examples :
If p = 1 et q = 1, Iq = [1, 3].
If p = 1 et q = 2, Iq = [10, 12].
If p = 2 et q = 1, Iq = [4, 6].
If p = 2 et q = 2, Iq = [13, 15]
If p = 3 et q = 1, Iq = [7, 9]
At the third spread, this block of 3 cards is divided into 3. After picking up column r and reforming the deck, card C is mechanically located in a block of only 1 card, whose position is :
Nr = 9(r - 1) + 1 + (Nq - 1)/3 = 1 + 9(r - 1) + 3(q - 1) + (p - 1), corresponding to the interval Ir = [Nr, Nr].
Examples :
If p = 1, q = 1 et r = 1, Ir = [1, 1].
If p = 1, q = 1 et r = 2, Ir = [10, 10].
If p = 1, q = 2 et r = 1, Ir = [4, 4].
If p = 1, q = 2 et r = 2, Ir = [13, 13].
If p = 2, q = 1 et r = 1, Ir = [2, 2].
If p = 2, q = 1 et r = 2, Ir = [11, 11].
If p = 2, q = 2 et r = 1, Ir = [5, 5].
If p = 2, q = 2 et r = 2, Ir = [14, 14].
If p = 3, q = 1 et r = 1, Ir = [3, 3].
Given the expression for Nr, the number N at the end of the trick satisfies the formula : N - 1 = 9(r - 1) + 3(q - 1) + (p - 1)
This trick is therefore simply a decoding of the number (N - 1) into base 3, column by column, where each column choice provides one of the three ternary digits.
Given this formula, the simplified expressions for p, q, and r are then as follows :
We set R = (N - 1) mod 9 + 1 = N - multiples of 9, adjusting R between 1 and 9
p = (N - 1) mod 3 + 1 = (R - 1) mod 3 + 1 = R - multiples of 3, adjusting p between 1 and 3 = column of the square p(R) in Figure above.
q = Ent[(N - 1)/3] mod 3 + 1 = Ent[(R - 1)/3] + 1 = column of the square q(R) in Figure above.
r = Ent[(N - 1)/9] + 1 = column of the rectangle r(N) in Figure above.
B6.3. Magic tricks with numbers :
Here are some spectacular number-based tricks.
B6.3.1. The Maurice Dagbert's trick :

[Heard on the radio in the 1980s]
A famous French calculating prodigy, Maurice Dagbert, presented this seemingly impossible problem :
"Choose an integer between 1000 and 3000 [2139 was given]. I will now calculate two lists of 17 integers each, such that :
- The sums of the numbers are equal to 2139,
- The sums of the squares of the numbers are equal,
- The sums of the cubes of the numbers are equal,
and so on up to the sixth power of the numbers.
Furthermore, all numbers will be different from each other, whether within a list or between lists."
For the number N = 2139 chosen, he then stated, after only a few minutes, the following two lists :
First list = [ 59, 63, 68, 82, 86, 100, 105, 109, 139, 143, 148, 156, 162, 173, 175, 185, 186 ]
Second list = [ 60, 61, 70, 79, 89, 98, 107, 108, 140, 141, 151, 153, 164, 170, 178, 183, 187 ]
A computer confirmed the calculations.
Explanation :
The problem can be written as the following system of equations S, with k = 6, n = 17, and Sum = N.
System S :
∑iai = ∑ibi = Sum
∑iai2 = ∑ibi2
∑iai3 = ∑ibi3
...
∑iaik = ∑ibik
where :
i = index from 1 to n
n = size of each list
k = power of the termes of last equation
Sum = sum of the terms of first equation
ai and bi = distinct integers to find for each of the two lists
First tip :
Each list of 17 numbers is actually a concatenation of two sublists of 8 and 9 numbers each, satisfying the following subsystems S1 and S2 :
Subsystem S1 = System S for k = 6, n = 8 and Sum = N1, corresponding to the following lists :
[ 59, 63, 68, 82, 86, 100, 105, 109 ] = [ 60, 61, 70, 79, 89, 98, 107, 108 ]
Subsystem S2 = System S for k = 6, n = 9 and Sum = N1, corresponding to the following lists :
[ 139, 143, 148, 156, 162, 173, 175, 185, 186 ] = [ 140, 141, 151, 153, 164, 170, 178, 183, 187 ]
Additional condition : N1 + N2 = N
Second tip :
Each subsystem is known in mathematics as the "PTE (or Prouhet-Tarry-Escott) Problem" [WIK1].
This problem has the remarkable property of being invariant under translation of variables [WIK1]. If we replace the variables ai and bi respectively with (α ai - β) and (α bi - β), where α and β are any two constants, then the new variables are solutions to the same problem by simply changing Sum to Sum* = (α Sum - n β).
This translation allows us to normalize the solutions, for example, by requiring that they be positive and that zero be included.
For S1, if we choose α1 = 1 and β1 = 84, we obtain the translated subsystem S1* as follows :
(1a) Subsystem S1* = subsystem S1 of sum N1* = N1 - 8 β1, corresponding to the following partial lists :
P1 = [ -25, -21, -16, -2, 2, 16, 21, 25 ]
Q1 = [ -24, -23, -14, -5, 5, 14, 23, 24 ]
This solution, called even-sized and symmetric [WIK1], is of the form [ -c4, -c3, -c2, -c1, c1, c2, c3, c4 ] for the first list and [ -d4, -d3, -d2, -d1, d1, d2, d3, d4 ] for the second.
This symmetry automatically makes equations in odd powers valid in subsystem S1a, which can be written as :
(1b) Subsystem S1* :
n = 4
∑ici2 = ∑idi2
∑ici4 = ∑idi4
∑ici6 = ∑idi6
corresponding to the following basic lists :
C1 = [ ci ] = [ 2, 16, 21, 25 ]
D1 = [ di ] = [ 5, 14, 23, 24 ]
For S2, if we choose α2 = 1 and β2 = 163, we obtain the translated subsystem S2* as follows :
(2a) Subsystem S2* = subsystem S2 of sum N2* = N2 - 9 β2, corresponding to the following partial lists :
P2 = [ -24, -20, -15, -7, -1, 10, 12, 22, 23 ]
Q2 = [ -23, -22, -12, -10, 1, 7, 15, 20, 24 ]
This solution, called odd-sized and symmetric [WIK1], is of the form [ -c5, -c4, -c3, -c2, -c1, d2, d3, d4, d5 ] for the first list and [ -d5, -d4, -d3, -d2, c1, c2, c3, c4, c5 ] for the second.
This symmetry automatically makes equations in even powers valid in subsystem S2a, which can be written as :
(2b) Subsystem S2* :
n = 5
∑ici = ∑idi
∑ici3 = ∑idi3
∑ici5 = ∑idi5
with d1 fictitious = 0
corresponding to the following basic lists :
C2 = [ ci ] = [ 1, 7, 15, 20, 24 ]
D2 = [ di ] = [ 0, 10, 12, 22, 23 ]
Furthermore, the symmetry of the solutions, for each subsystem S1a and S2a, makes the sums N1* and N2* zero, which can be written :
(3) N1 = 8 β1 and N2 = 9 β2
Hence the necessary condition : N = N1 + N2 = 8 β1 + 9 β2
Note that this condition is always attainable, since 8 and 9 are coprime.
Choice of a solution for subsystem S1b :
Subsystem S1b is that of the PTE problem of size n = 4 and specific powers k = 2, 4, and 6.
Several solutions have been known since 1913, including the following [SHU1] :
[ 2, 16, 21, 25 ] = [ 5, 14, 23, 24 ]
[ 7, 24, 25, 34 ] = [ 14, 15, 31, 32 ]
[ 7, 31, 36, 50 ] = [ 18, 20, 41, 49 ]
[ 9, 47, 49, 67 ] = [ 23, 31, 61, 63 ]
The first solution is the smallest solution in non-negative integers for these three powers [SHU2].
It is highly probable that Maurice Dagbert knew these solutions and used the first one.
Choice of a solution for subsystem S2b :
The S2b subsystem corresponds to the PTE problem of size n = 5 and specific powers k = 1, 3, and 5.
While published solutions are scarce, they can be found analytically. The approach involves pairing elements from the two lists and then solving the resulting quadratic system using an appropriate method, such as variable elimination or the method of discrete orthogonal moments [WIK2][SAY].
Both approaches rely on the analytical solution of an underdetermined quadratic system of rank 2 with 5 variables, producing a family of real solutions, complemented by a short phase of targeted successive trials aimed at achieving integer values that exactly satisfy the equations.
The steps are as follows :
1. We arbitrarily fix 5 small integer values δi (for example, between -3 and 3) such that ∑i[δi] = 0 with δi = ci - di
2. We set xi = mi2 with mi = ((ci + di)/2)2 corresponding to the local center of the variables ci and di, which induces : xi # ci2 # di2 # ci di
where the symbol "#" means "very little different"
3. Given the identities : (c3 - d3) = (c - d)(c2 + c d + d2) et (c5 - d5) = (c - d)(c4 + c3 d + c2 d2 + c d3 + d4), equations S2b become :
∑ici - ∑idi = ∑i[δi] = 0
(∑ici3 - ∑idi3 # 3 ∑i[δi xi]) = 0
(∑ici5 - ∑idi5 # 5 ∑i[δi xi2]) = 0
4. We solve the quadratic system (∑i[δi xi] = 0) and (∑i[δi xi2] = 0) using one of the methods mentioned above, which gives a family of real solutions.
Solution by elimination of variables :
We fix 3 free variables, for example x1, x2 et x3
We then eliminate x4 between the two equations, which gives an equation of the form : A x52 + B x5 + C, where A, B, and C are explicit quadratic polynomials in x1, x2 et x3
We find the real solution : x5 = [-B ± √(B2 - 4 A C)]/(2 A), and x4 is obtained from the equation (∑i[δi xi] = 0).
5. We look for xi close to the square of an integer or a half-integer, which gives di then ci = di + δi
6. We substitute ci et di into the exact equations (2b) for verification.
7. If the initial result is not verified, further tests are performed by modifying the parameters at two possible levels :
- Exploration of the 3 free parameters xi.
- Selection of the deviation vector δi.
It is highly probable that Maurice Dagbert himself obtained the basic lists (2b) using this simple method.
Calculation of β1 and β2 from a given N :
Condition (3) is a Diophantine equation that can be written more simply as :
(4) β1 = 9 u - N and β2 = N - 8 u, with u arbitrary
But it is also necessary to ensure the connection of the lists of subsystems S1 and S2, in order to give the illusion of two unique and increasing lists of 17 numbers each, which, considering lists (1a) and (2a), can be written as :
(25 + β1) less than and close to (-24 + β2)
(24 + β1) less than and close to (-23 + β2)
Given relations (4), these two relations are equivalent to :
(β2 - β1) = (2 N - 17 u) greater than and close to 47
which gives a maximum for u :
(5) u max = (2 N - 47)/17
For N = 2139, u max = 248,9
Maurice Dagbert chose u = 247, resulting in values of 84 and 163 for β1 et β2.
Construction of the lists of 17 numbers :
The two lists of 17 numbers provided by Maurice Dagbert are then established in four steps :
1. Calculation of u according to relation (5).
2. Calculation of β1 and β2 according to relations (4).
3. Memorization of three lists of gaps based on the gaps between consecutive numbers in each translated list P1, Q1, P2, Q2 (see relations (1a)(2a)) :
List of gaps E1 = [ 4, 5, 14, 4, 14, 5, 4]
List of gaps E2 = [ 4, 5, 8, 6, 11, 2, 10, 1 ]
List of gaps E3 = [ 1, 9, 9, 10, 9, 9, 1 ]
4. Creation of the two lists of 17 numbers based on these lists of gaps and the translations β1 and β2, according to the following distribution :
First list of 17 numbers = [P1, P2]
Second list of 17 numbers = [Q1, Q2]
with :
P1 = [ (β1 - 25), +E1 ] composed of 8 terms
P2 = [ (β2 - 24), +E2 ] composed of 9 terms
Q1 = [ (β1 - 24), +E3 ] composed of 8 terms
Q2 = [ (β2 - 23), +E2! ] composed of 9 terms
The symbol "!" means that the list must be read in reverse.
Note : There is another (more complicated) way to create the two lists of 17 numbers, based on memorizing the elementary lists C1, D1, C2, D2 (see relations (1b)(2b)) :
First list of 17 numbers = [ (β1 - C1!)4, (β1 + C1)4, (β2 - C2!)5, (β2 + D2°)4 ]
Second list of 17 numbers = [ (β1 - D1!)4, (β1 + D1)4, (β2 - D2°!)4, (β2 + C2)5 ]
The symbol "°" means that the fictitious term 0 in the list should be ignored.
The subscript at the bottom indicates, as a reminder, the number of terms in the quantity within the parentheses.
No duplicates in a list or between lists of 17 numbers :
This remarkable property results from three observations :
- By construction, the basic lists C1 and D1 have no duplicates, either internally or between themselves. Therefore, the same is true for the translated lists P1 and Q1, given their symmetries.
- Also by construction, the basic lists C2 and D2 have this same property. Therefore, the same is true for the translated lists P2 and Q2, given their symmetries.
- By deliberate choice, the lists P1 and P2 are disjoint, as are the lists Q1 and Q2 (see condition (5)).
Consequently, the two lists of 17 numbers cannot have any duplicates, either internally or between themselves, since they result from the simple concatenation of P1 and P2 for the first and of Q1 and Q2 for the second.
B6.4. Sources :
[ASH] ashmarlow52, Learn This Viral Battery Trick (Youtube, 01:07).
[CAR1] Carrefour francophone, Cours de Magie avec Magislain - Tour 4 : Evasion (Youtube, 03:16).
[CAR2] Carrefour francophone, Cours de magie avec Magislain - Tour 2 : L'élastique à travers les doigts (Youtube, 03:21).
[EIT] Joseph Eitel, The Handcuff Escape Puzzle.
[GAR] Nasr Garouachi, Cordes - Playlist.
[HAF] Nadjib Haffaf, Echapper à la corde facile - DIDACTICIEL (Youtube, 02:45).
[JER] Jérémie-L'école de la magie, 3 TOURS DE MAGIE AVEC 1 ELASTIQUE (Youtube, 08:20).
[MAGE] MagieExpliquée, Apprenez la Téléportation avec un simple Elastique - Secret Révélé (Youtube, 06:43).
[MIR] Minute Facile, Régis le magicien vous explique son incroyable tour de magie avec une corde (Youtube, 03:50).
[PAU] Paulo magie, apprenez un tour impressionnant avec 2 élastiques (Youtube, 05:26).
[PRA] pratiqueTV, Tour de passe passe avec des piles (Youtube, 01:50).
[SAY] Sayyouri M., Contributions en analyse d'image par les moments orthogonaux discrets, Thèse, 2014.
[SHU1] Chen Shuwen, Non-negative Integer Solutions of a1k + a2k + a3k+ a4k = b1k + b2k + b3k + b4k ( k = 2, 4, 6 ).
[SHU2] Chen Shuwen, On the Generalization of the Prouhet-Tarry-Escott Problem.
[TUT] TUTO MAGIE, TOUR DE MAGIE FACILE AVEC UN ELASTIQUE EXPLICATION (Youtube, 04:48).
[VAL] TUTUR VAL, 5 TOURS DE MAGIE AVEC DES ELASTIQUES (Youtube, 07:49).
[WIK1] Problème de Prouhet-Tarry-Escott.
[WIK2] Wikipedia, Suite de polynômes orthogonaux.
See detail.
Constellations, apparent groupings of stars forming imaginary figures in the sky, have fascinated humanity for millennia.
Today, 88 official constellations are used to map the sky. Some, such as The Little Bear or Cassiopeia, are visible all year round, while others, such as The Swan in summer or Orion in winter, are only revealed in certain seasons.
The zodiacal constellations, crossed by the Sun during the year, are part of these 88 official ones and play a special role in astrology.
Observing the sky also reveals remarkable stars, such as Sirius or Vega, real landmarks in the celestial vault. To make the most of them, it is then important to follow certain practical observation tips.
C4.1. General information [CHA][PER] :
Definitions :
- A constellation is an apparent grouping of stars in the night sky as seen from Earth.
- A circumpolar constellation is one that, for an observer at a given latitude (north or south), remains visible year-round.
- A seasonal constellation is a non-circumpolar constellation, therefore visible only during or around a given season, and absent from the night sky the rest of the year.
- The ecliptic is the plane of the Earth's orbit around the Sun or, as seen from Earth, the circle traced by the Sun on the celestial vault over the course of a year.
- The horizon is the horizontal circular line where the sky and the Earth (or the sea) appear to meet.
- The zenith is the point in the sky located exactly vertically above the observer's head.
- The North Celestial Pole is the point in the sky located above the northern horizon, at a height equal to the observer's latitude. For Paris (approximately 49° north latitude), on a rotating disk sky map, this point appears halfway between the center of the disk (zenith) and its northern edge (northern horizon). To use the disc correctly, it must be held above the head and the northern edge of the disc must be oriented towards geographic north, using a compass for example.
- Warning : On a sky map, the east and west directions are reversed compared to a traditional map, in order to correspond to the viewpoint of the observer holding their map towards the sky. Turning a map over (putting it upside down) while keeping north in front of you effectively reverses right and left.
- The North Star (Polaris) is an excellent representative of the celestial north pole, through which the Earth's own rotational axis passes. The angular difference between these two points (approximately 0°38' in 2025) is in fact imperceptible to the naked eye because the north celestial pole is only an abstract point in the sky, located very close to Polaris.
Movement and position of the constellations :
- The movement of the constellations is as follows : Due to the daily rotation of the Earth on its axis, all the constellations visible from the northern hemisphere describe a circle around Polaris in 24 hours, counterclockwise, but only the circumpolar ones remain visible at all times. The seasonal ones pass below the horizon during their rotation, rising in the east and setting in the west each day.
- The relative geometric position between constellations, as well as between stars in the same constellation, does not change significantly during the Earth's daily rotation (diurnal motion) or during its annual revolution around the Sun (seasonal motion). This is explained by the very great distance between Earth and the stars in these constellations. Only the portion of the sky visible from a given location on Earth at a given time changes.
- The "open hand" is a good guide to measuring the distance between two points in the sky : Hold your hand at arm's length, fingers spread, and consider the width extending from the tip of your thumb to the tip of your little finger. This width corresponds to an angular difference of about 20° measured from the observer.
Stars, planets, the Moon, artificial satellites, aircraft, shooting stars, star cluster :
- Stars twinkle. This phenomenon is due to the turbulence of the Earth's atmosphere that disrupts the light coming from these very distant point sources.
- The planets of the solar system, on the other hand, do not twinkle or twinkle very little. They are in fact much closer to Earth and appear to the naked eye as points of light just like stars, and to the telescope as small luminous discs.
- The planets and the Moon only pass through the constellations of the astronomical zodiac, never the circumpolar constellations or the non-zodiacal seasonal constellations. Indeed, the planets and the Moon always remain very close to the ecliptic, while these constellations are located far from the ecliptic (circumpolar ones around the celestial pole, north or south, non-zodiacal seasonal ones elsewhere in the sky).
- The planets and the Moon are not circumpolar : They rise and set every day, while gradually moving relative to the distant stars in the background sky. The Moon moves about 13° eastward each day relative to these stars and therefore takes 27.3 days to complete one apparent orbit around the North Star. The planets move much more slowly and take several years, depending on the planet, to complete one orbit.
- The Moon is absent from the night sky during nights close to the new moon at certain times (see
Tips for good observation), which allows optimal observation of the constellations.
- Artificial satellites in low Earth orbit appear as a white, non-blinking point of light that crosses the sky from west to east in a few minutes.
- Aircraft flying at high altitudes appear as a flashing white point of light (anti-collision strobe light), which moves more slowly than artificial satellites. At medium or low altitudes, aircraft are distinguished by several fixed colored points of light (position lights), in addition to the flashing white point, all of which can appear separate or merged depending on the distance from the observer.
- Shooting stars (or meteors) are luminous trails visible for one to two seconds. They come from dust clouds left by comets or asteroids. Each year, the Earth crosses the orbit of these clouds, causing their dust to burn up upon contact with the Earth's atmosphere. On average, 5 to 10 shooting stars are observed per hour, and up to 50 to 100 during peak activity of these meteorite clouds, particularly between mid-July and mid-August in the constellation of Perseus, and early to mid-December in the constellation of Gemini.
- A star cluster is a local grouping of stars bound together by gravity, born from the same region of gas and dust within the same galaxy. Seen from Earth, it appears projected into a constellation.
Brightest objects :
The brightest natural objects in Earth's night sky, visible from the Northern Hemisphere, are as follows, in descending order of brightness :
C4.2. List of constellations :
The International Astronomical Union (IAU) defined 88 official constellations in 1922 [IAU1]. They cover the entire celestial sphere, divided between the northern and southern hemispheres.
They are distributed as follows :
* 54 constellations visible totally or partially from Metropolitan France
- 7 constellations visible all year round
- 20 seasonal constellations visible during the extended summer (May to October)
- 15 seasonal constellations visible during the extended winter (November to April)
- 12 constellations that are difficult to see with the naked eye
* 34 constellations not visible from Metropolitan France
The 54 constellations visible totally or partially from Metropolitan France are as follows, listed in alphabetical order :
These constellations are described below, classifying them by period of year and then by position in the sky, according to the following definitions :
|
In synthesis, the constellations are then precisely located in the sky according to a neutral representation that uses neither cardinal points, nor relative directional notions, nor the observer's position on Earth, nor reference to the hour or day of the year. This method of celestial location, developed by the Author, relies exclusively on the following principles : - The initial identification of major stars or constellations, visible and recognizable without error to the naked eye. - The construction of imaginary straight lines between these celestial landmarks, allowing for recursive triangulation : Each new landmark is located by geometric alignment with the landmarks already identified, which gradually expands the mental map of the sky. - The estimation of apparent angular distances using the width of an open hand held at arm's length, used as a natural and universal unit of measurement. This pragmatic method is particularly suited to progressive learning of visual astronomy and celestial navigation without instruments. |
C4.3. Constellations visible all year round
:
The constellations visible from Metropolitan France all year round (circumpolar constellations) are as follows (see Figures below [IST][LES]) :
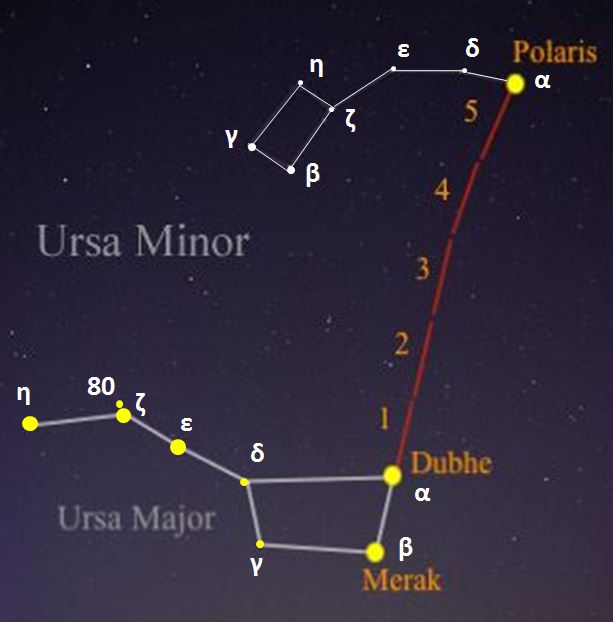





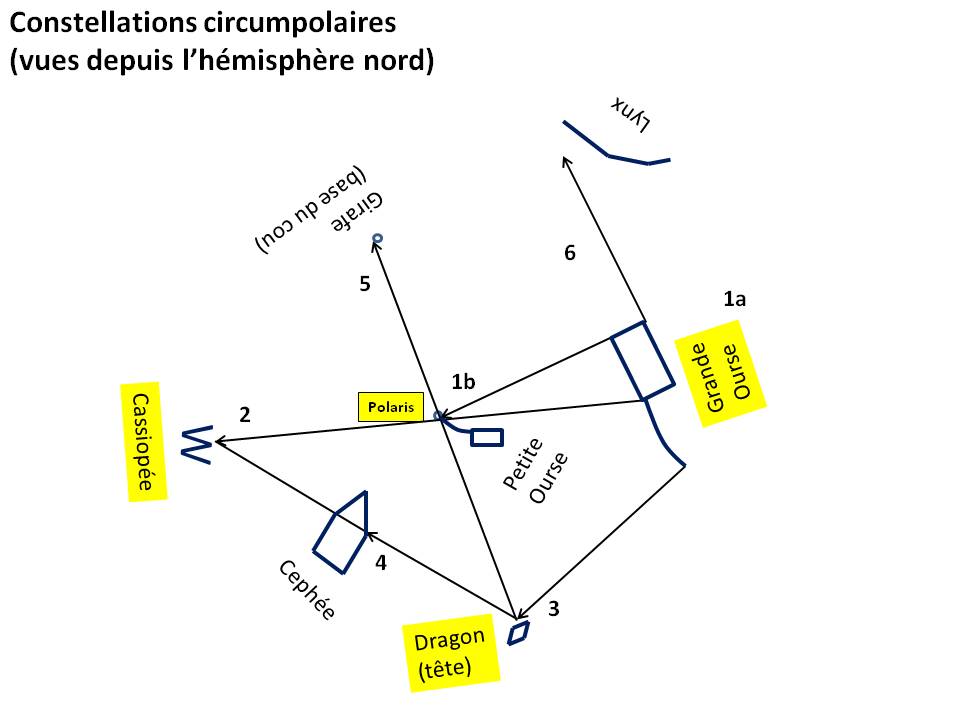
|
Synthesis : To find these constellations in the sky, the simplest method is as follows [DAR][CHA][PER], by referring to the maps above : - Map from July 25, 2025 at 00:00 for mainland France or latitudes from 40 to 55°N, with zenith at the center of the portion of visible sky [STE]. - Guide to locating circumpolar constellations (in neutral representation). 1a. Find The Great Bear : Large dipper with seven bright stars, located in the northern half of the sky. Its height is low (near the horizon) in autumn and winter, and very high (near the zenith) in spring and summer. Its length, from the handle end (η) to the outer edge (α or β) of the dipper, is one open hand width. 1b. Find the North Star Polaris : Bright star located near the Great Bear in the extension of the outer edge of the dipper, in the opposite direction to its bottom, at a distance equivalent to an open hand width or five times the distance between the two stars (α and β) on this edge (see Figure 1 above). Find The Little Bear : Small dipper with three bright stars, including Polaris (α) at the end of the handle and two stars (β and γ) at the outer edge of the dipper (see Figure 1 above). The four intermediate stars (δ, ε, ζ, η) are often not very visible. 2. Find Cassiopeia : Characteristic W shape, located opposite the center of the Great Bear (attachment point of the dipper handle) from Polaris. 3. Find The Dragon : Its head is a distorted square of four bright stars (γ β, ν, ξ) located near the Great Bear, two open hand widths apart, by drawing from the end (η) of the dipper handle a perpendicular in the direction in which the handle is curved. The body (δ, ζ, η, ι, α) and tail (λ) of the Dragon form a large inverted S (as seen in a mirror) of six bright stars that partially wraps between the Great Bear and the Little Bear. 4. Find Cepheus : Polygon with seven bright stars forming a child's house (rectangle α, β, ι, ζ) with pointed roof (γ), located halfway between Cassiopeia and The Dragon's head. 5. Find The Giraffe : Group of nine stars including a long neck (α, HD 42818, HD 49878, VZ) pointing towards Polaris. The brightest star (β) is located opposite the Dragon's head from Polaris. 6. Find The Lynx : Broken line of seven stars including three bright ones (α, 38, 10 UMa), fully visible in late winter and spring, located near the Great Bear, one open hand width apart, in line with the bottom of the dipper, in the opposite direction to the handle. |
C4.4. Summer seasonal constellations :
The seasonal constellations visible from Metropolitan France during the extended summer (May to October) are the following (see Figures below [IST][LES]) :

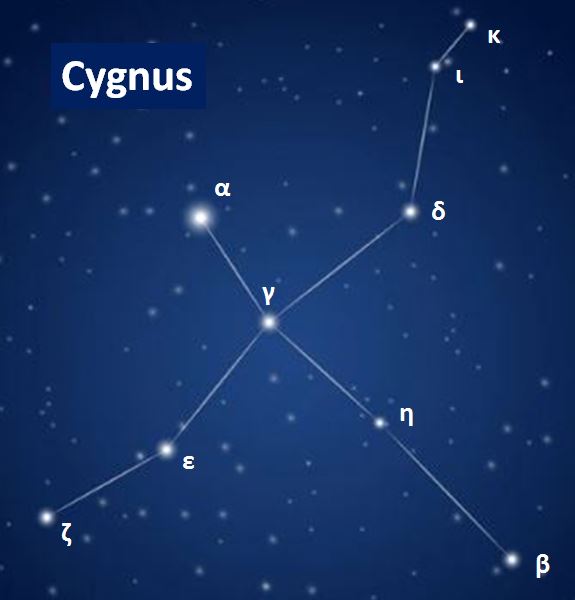
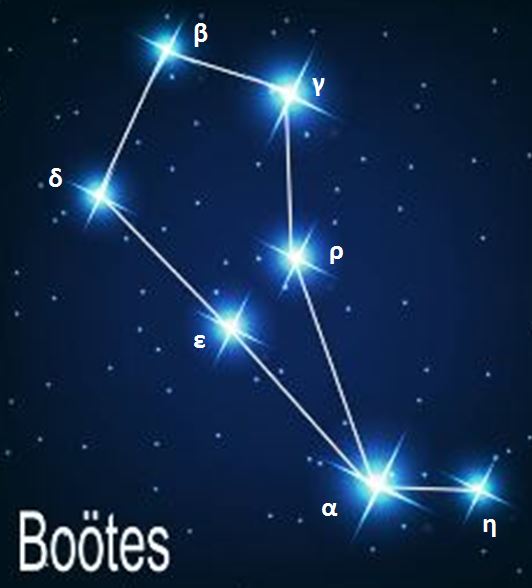

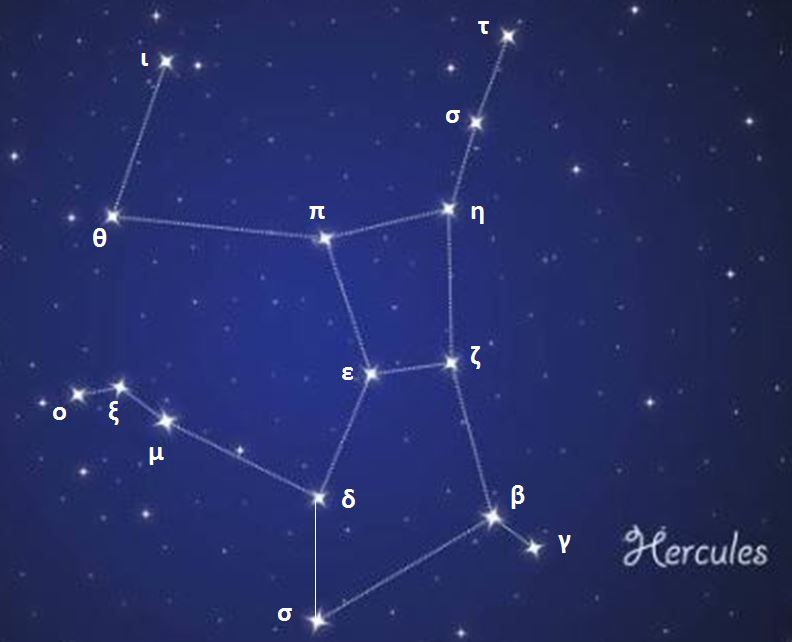
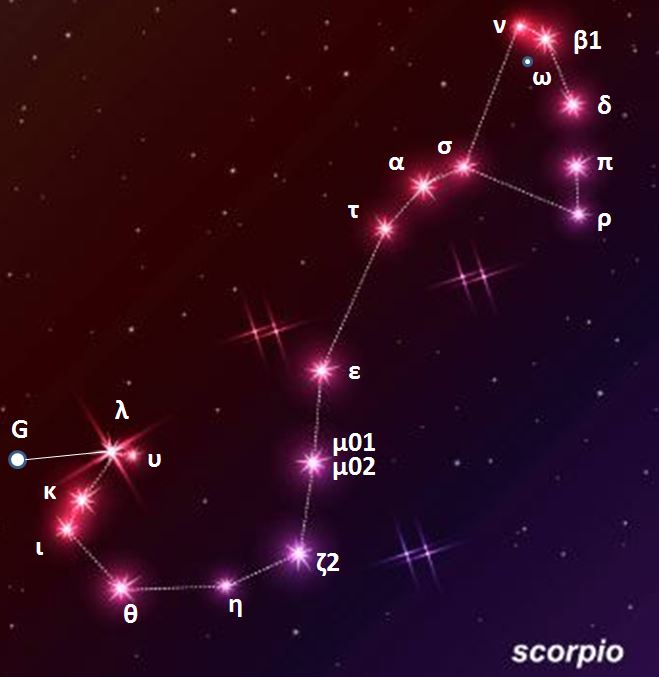
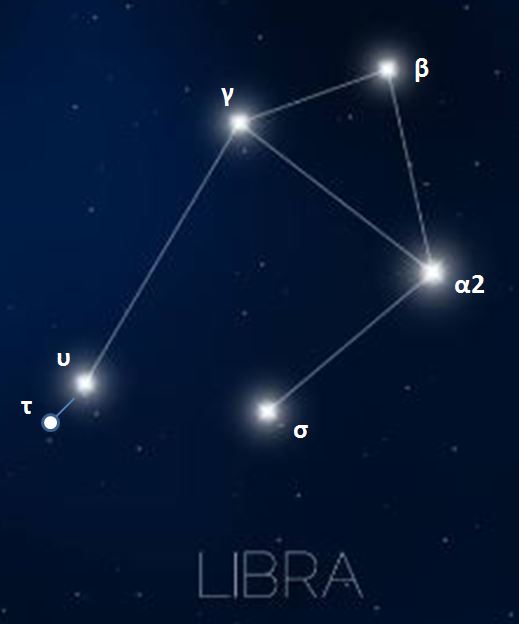
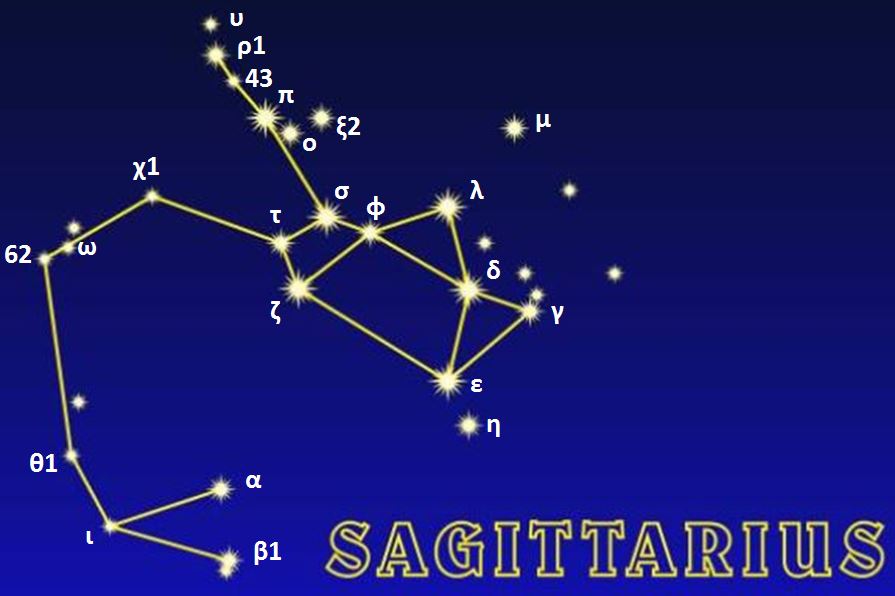
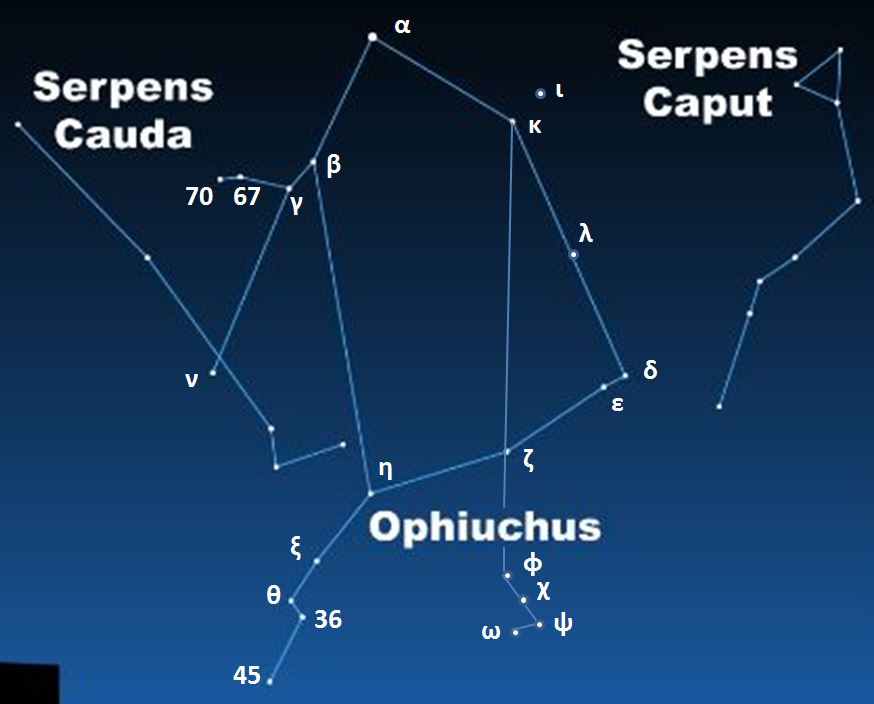
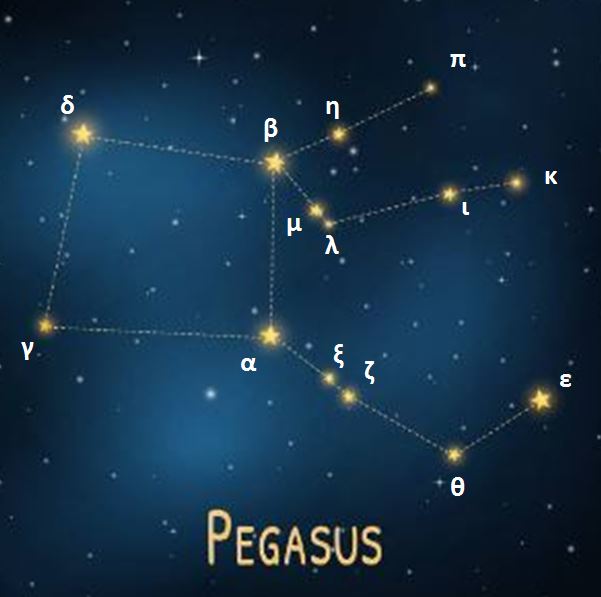
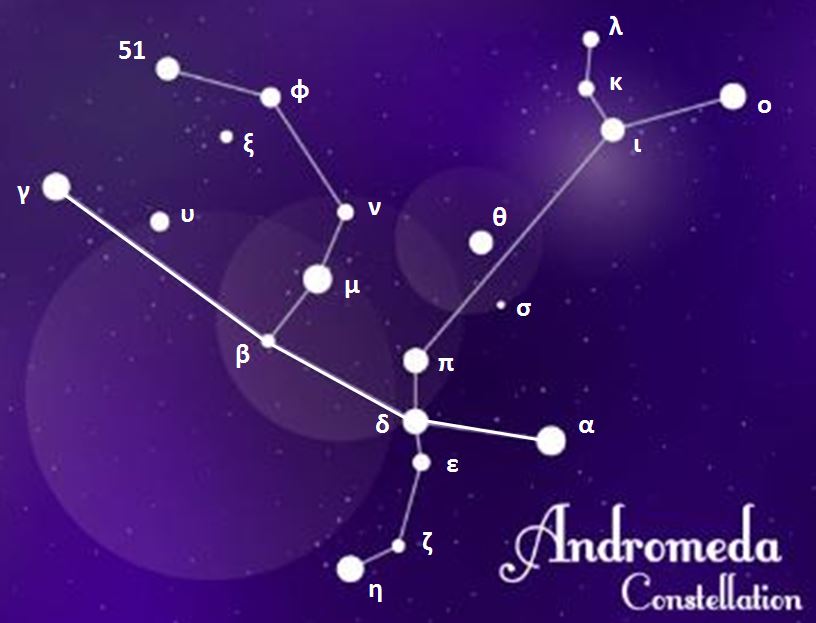

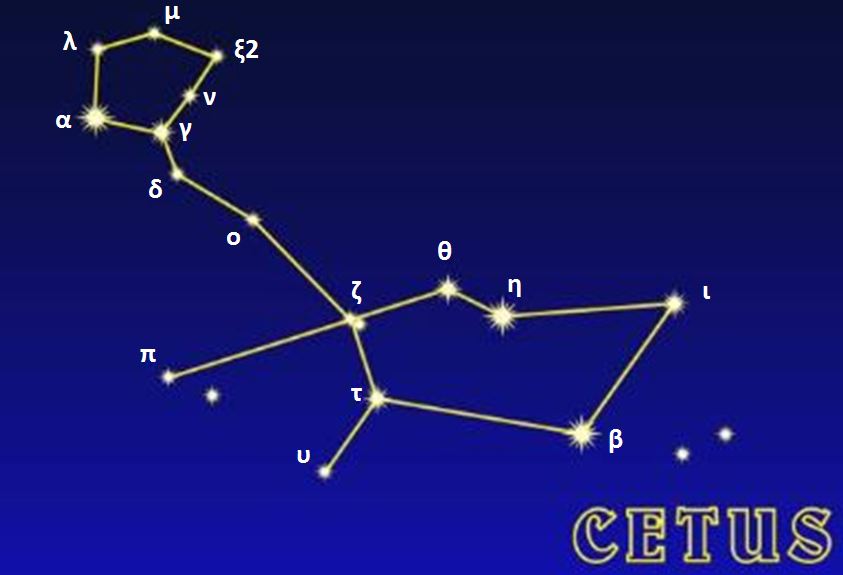

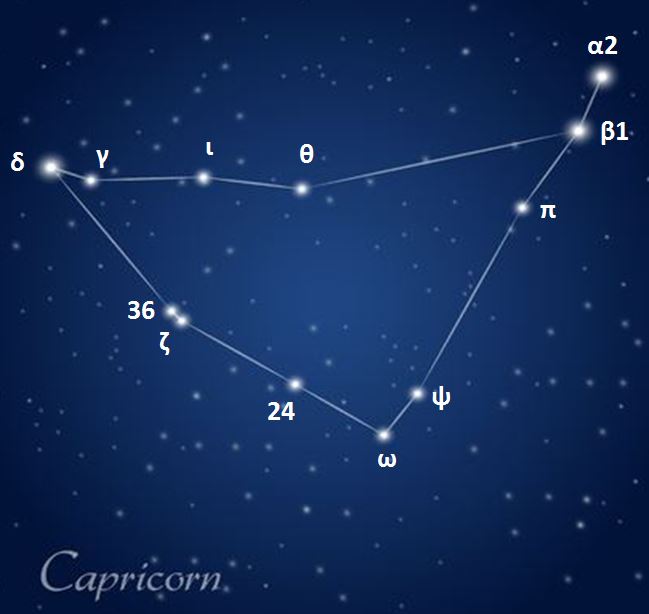

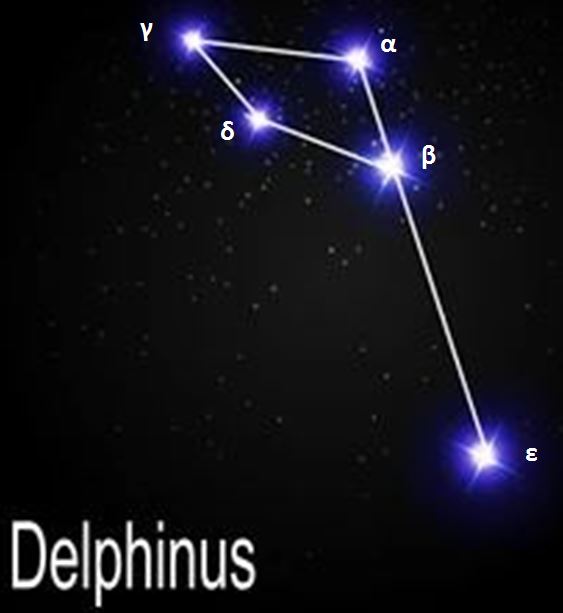
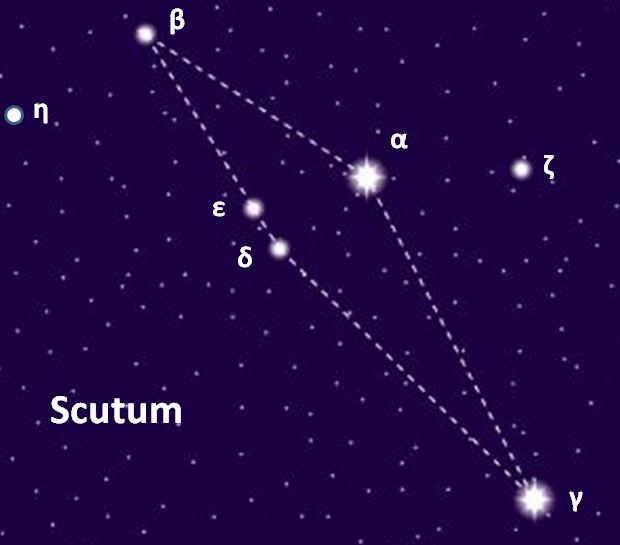
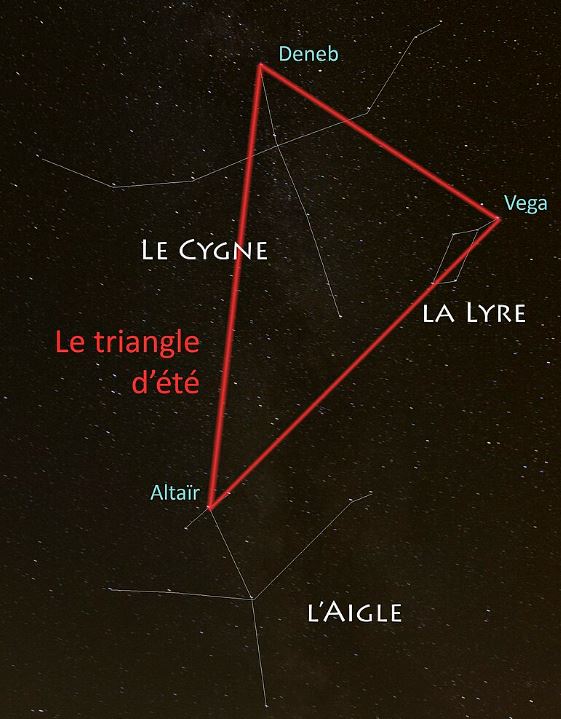

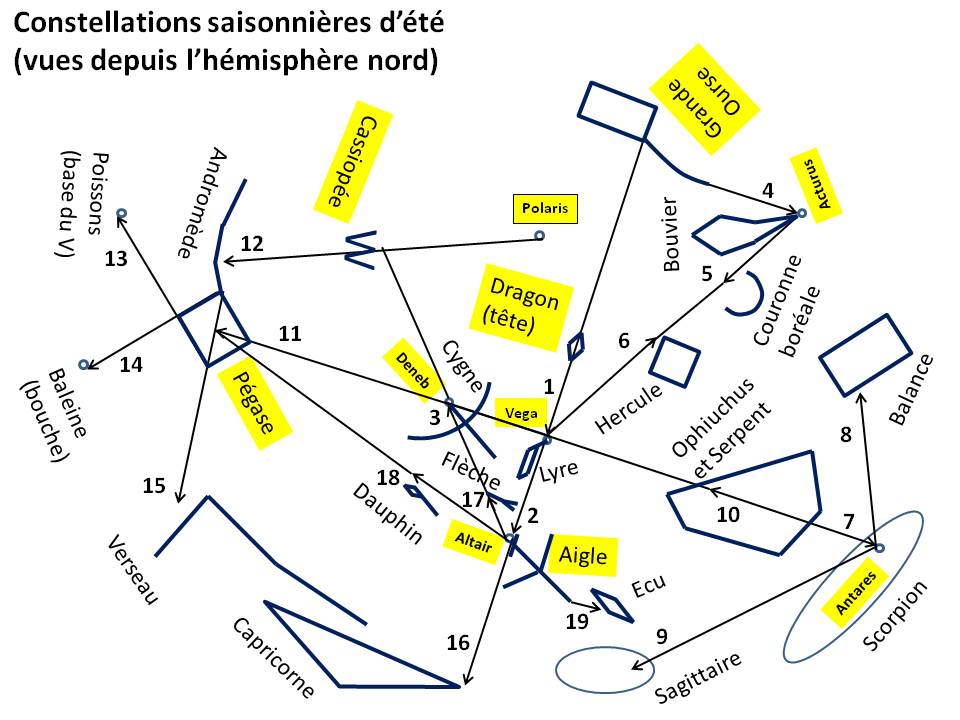
|
Synthesis : To find these constellations in the summer sky, the simplest method is the following [CHA][PER], by referring to the maps above : - Summer Triangle. - Map of July 25, 2025 at 00:00 for mainland France or latitudes from 40 to 55°N, with zenith at the center of the portion of visible sky [STE]. - Guide to locating summer seasonal constellations (in neutral representation). 0. Find the Summer Triangle located near the zenith around midnight in summer (July to September) : Quasi-equilateral triangle formed by three super-bright stars : Vega (Lyra), Altair (Eagle) and Deneb (Swan). The distance between each star is one width of an open hand. 1. Find the star Vega, a brightest star in the Summer Triangle, blue-white in color. Vega is located near the Dragon's head, on a line coming from the end of Great Bear's handle and passing through the Dragon's head. in line with and opposite the Great Bear. Find The Lyre : Small parallelogram of four stars including two bright ones (β, γ), connected to Vega (α) and extending this line from Vega. 2. Find the star Altair, a star of the Summer Triangle, flanked by two smaller stars (β and γ), located near Vega, one open hand width apart, on a line coming from the end of Great Bear's handle and passing through Vega. Find The Eagle : Large figure located to the left of this line when arriving at Altair (α), composed of a head (γ-α-β) centered on Altair, two straight wings (δ-ζ and δ-θ) turned towards the head, a linear body (α-δ-λ) and a tail (λ). 3. Find the star Deneb, a star of the Summer Triangle, located to the right of the line from Vega to Altair, and also halfway between Altair and Cassiopée. Find The Swan : Large cross composed of a tail (α, Deneb), a body (α-γ), two broken wings (γ-ε-ζ and γ-δ-ι) turned towards the tail, a long neck (γ-η-β) turned towards Altair, and a head (β). 4. Find the star Arcturus, a super-bright, orange star located in line with the handle of the Great Bear, one open hand width apart. Find The Herdsman : Group of seven bright stars in the shape of a kite, located to the right of this line before reaching Acturus (α). 5. Find The Northern Crown : Semicircle of seven stars including three bright ones (α, β, γ), located near Arcturus to the left of the line from Arcturus to Vega. 6. Find Hercules : Group of fourteen bright stars, four of which form a square (ε, ζ, π, η) located near Vega to the left of the line from Arcturus to Vega. 7. Find the star Antares, a super-bright, isolated, red star, located very low on the southern horizon, visible from May to August., on a line coming from Deneb and passing through Vega, three open hand widths apart from Vega. Find The Scorpion : Large S with nineteen bright stars surrounding Antares (α), the heart of the Scorpion, with its two small pincers (β1 - δ et ρ - π) located west of Antares (to the left of the line from Vega to Antares). 8. Find The Scales : Polygon with six bright stars, four of which form a rectangle (α2, β, γ, σ), located west of Antares (to the left of the line from Vega to Antares), one open hand width apart from Antares. 9. Find Sagittarius : Group of fifteen bright stars located east of Antares (to the right of the line from Vega to Antares), two open hand widths apart from Antares. 10a. Find Ophiuchus : Polygon of twelve bright stars, three of which form an irregular pentagon (α, β, η, ζ, δ) located halfway between Antares and Vega. 10b. Find The Serpent : Group of bright stars located on either side of Ophiuchus (six for The Serpent's Head forming a Y and one for The Serpent's Tail). 11. Find Pegasus : Group of eleven bright stars, four of which form a large empty square (α, β, γ, δ) located near Deneb, two open hand widths apart, on a line coming from Vega and passing through Deneb. 12. Find Andromeda : Group of eight bright stars touching Pegasus, four of which form a broken line located opposite Polaris from Cassiopeia. 13. Find The Fishes : Large V with three bright stars. Its base (α Piscium) is located in the extension of one of the sides of the large square of Pegasus as follows: 1. Identify the brightest star (δ) of the square, 2. Identify the corner (α) diagonally opposite, 3. Identify the next corner (γ) clockwise from α, 4. Extend the line α-γ over a distance equivalent to one open hand width. 14. Find The Whale : Polygon of six bright stars extended by a line of three other bright ones. The mouth (β) of the Whale, the brightest star, is located in the extension of one of the sides of the large square of Pegasus as follows : 1. Identify the brightest star (δ) of the square, 2. Identify the next corner (γ) counterclockwise from δ, 4. Extend the line δ-γ over a distance equivalent to one open hand width. 15. Find The Water Bearer : Group of eight bright stars, four of which form a broken line (δ, α, β, ε) located in the extension of a diagonal of the great square of Pegasus as follows : 1. Identify the brightest star (δ) of the square, 2. Identify the diagonally opposite corner (α), 3. Extend the line δ-α over a distance equivalent to one open hand width. 16. Find The Sea Goat : Flattened triangle with eight bright stars, located opposite Vega from Altair. 17. Find The Arrow : Arrow with four stars including two bright ones (γ, δ), located near Altair to the right of the line from Altair to Deneb. 18. Find The Dolphin : Small diamond with five stars including two bright ones (α, β), extended by a tail (ε) and located near Altair to the left of the line from Altair to Pegasus. 19. Find The Shield : Small elongated diamond with four stars including a bright one (α), located near the Eagle's tail (λ). |
C4.5. Winter seasonal constellations :
The seasonal constellations visible from Metropolitan France during the extended winter (November to April) are the following (see Figures below [IST][LES]) :


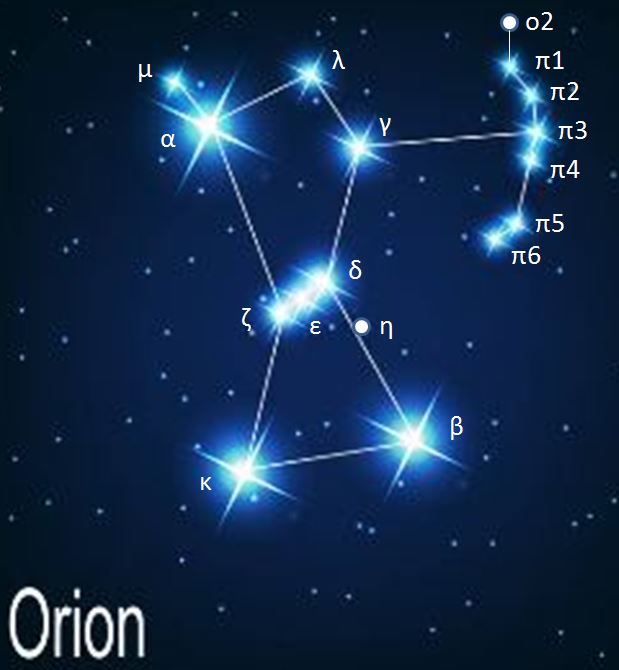
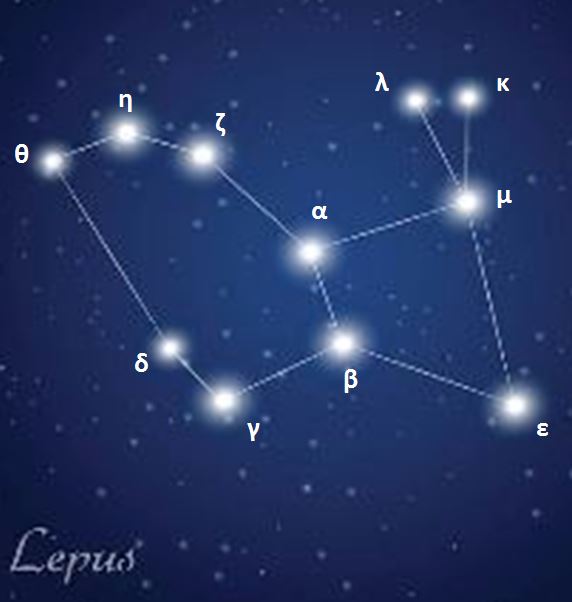
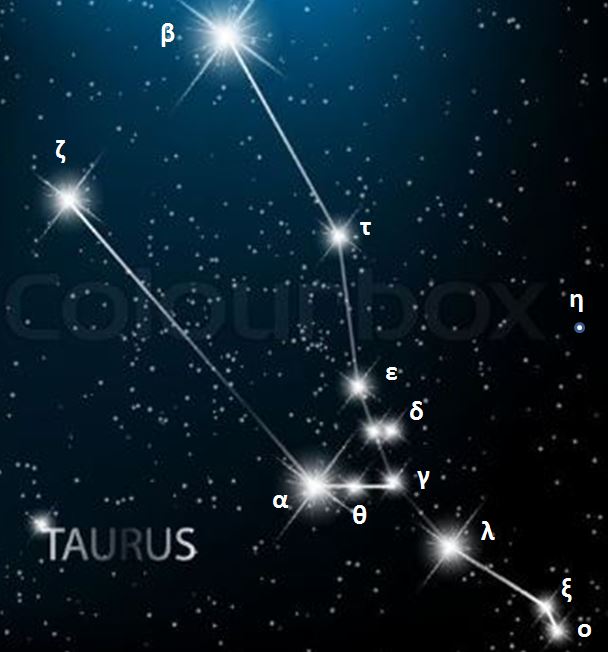
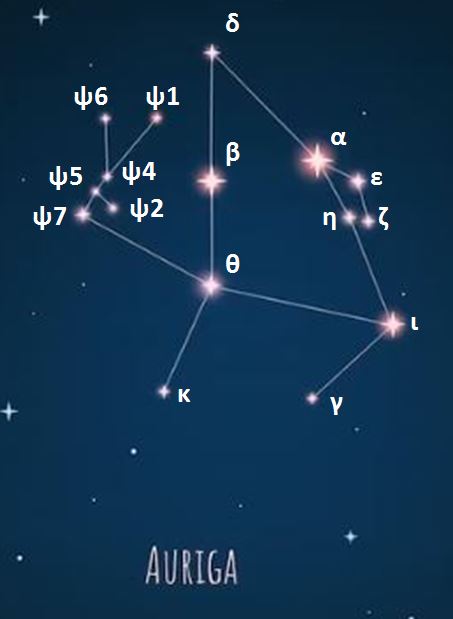

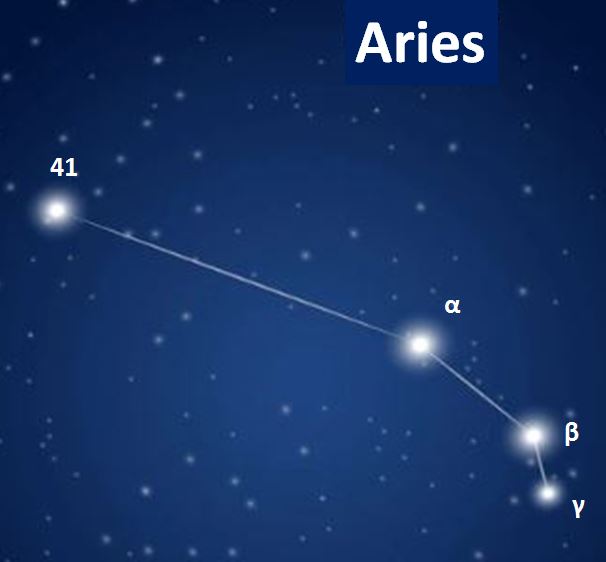
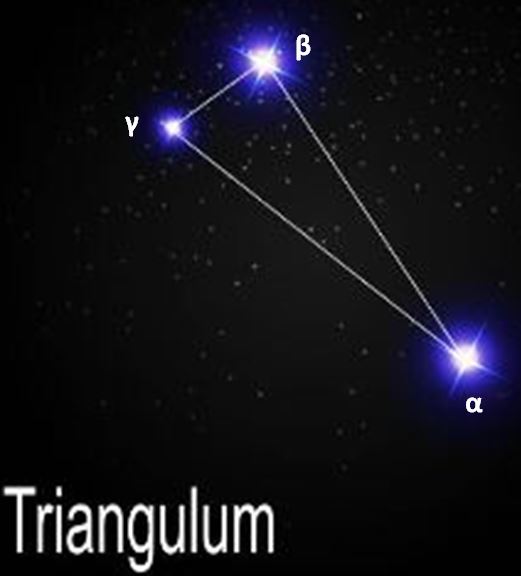



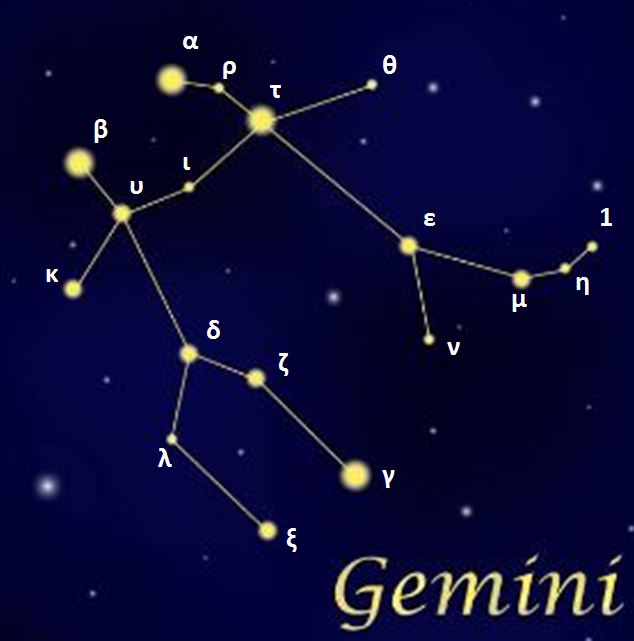
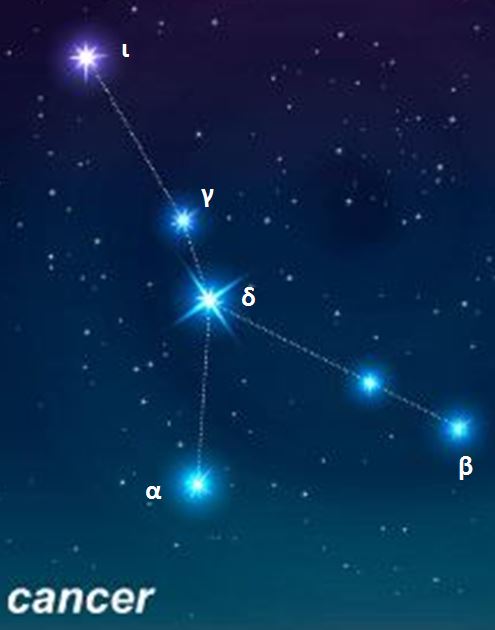
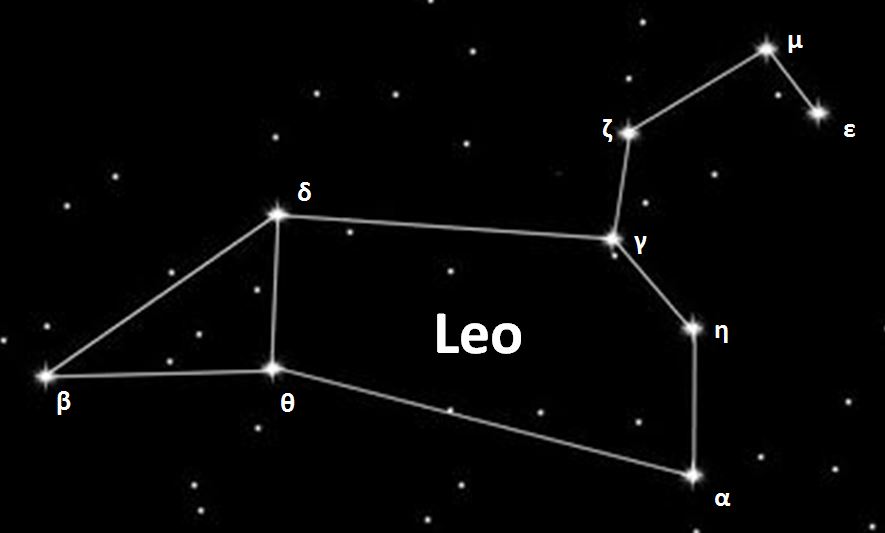
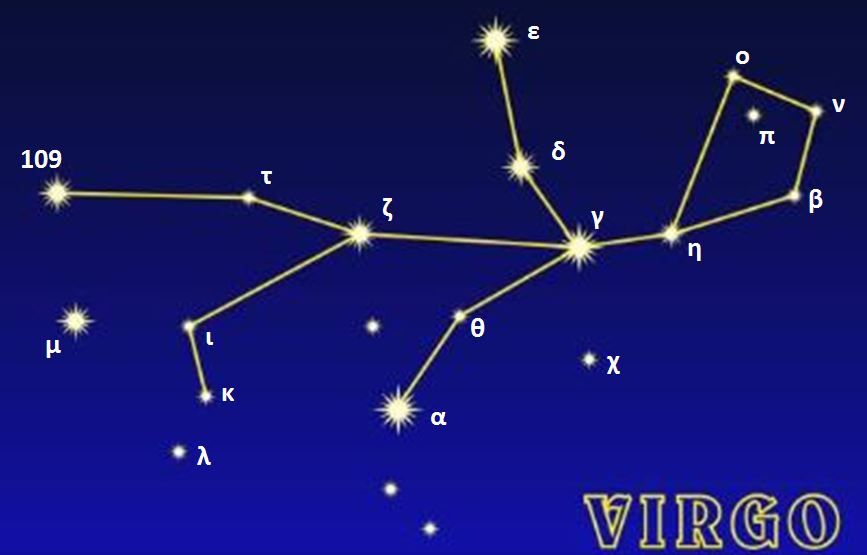
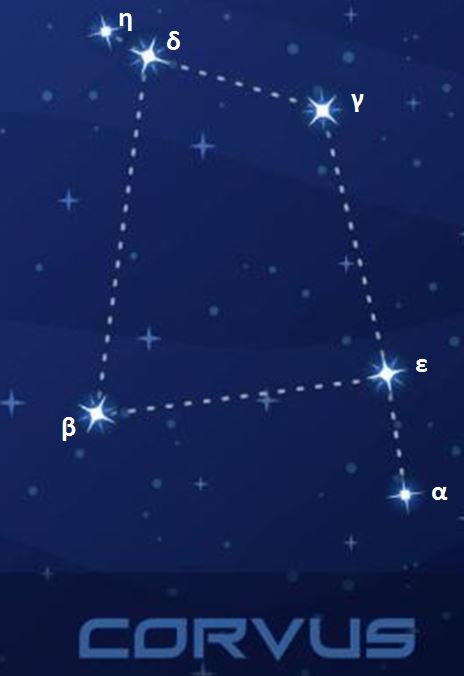
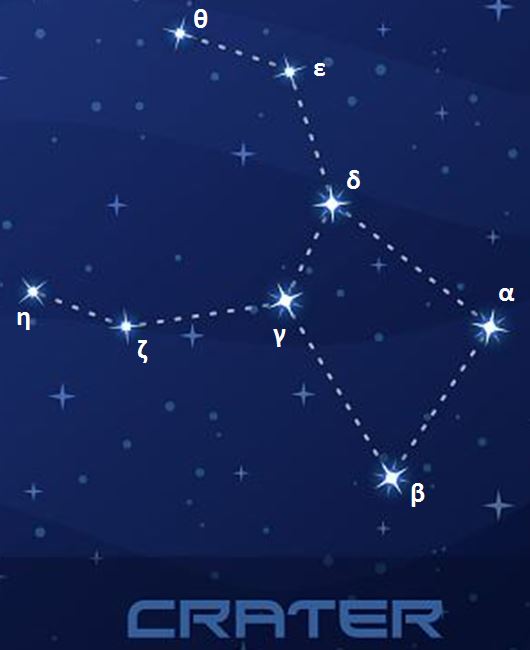
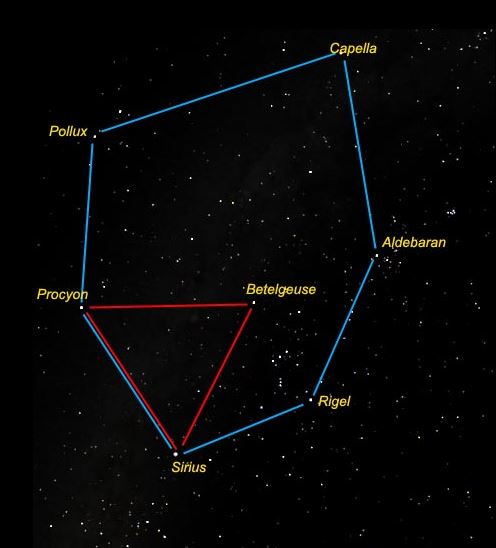
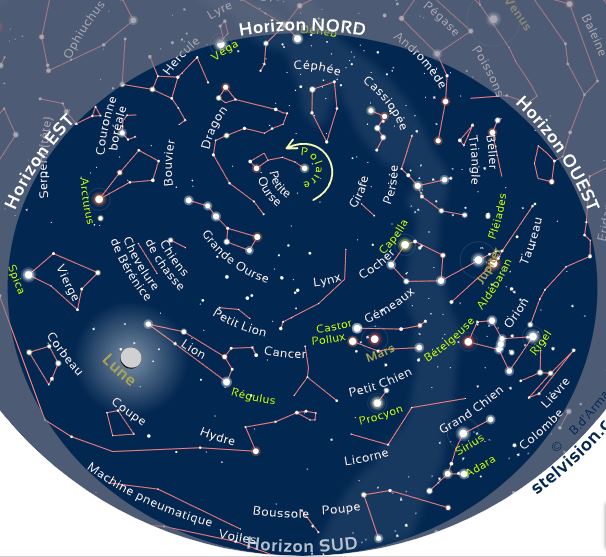
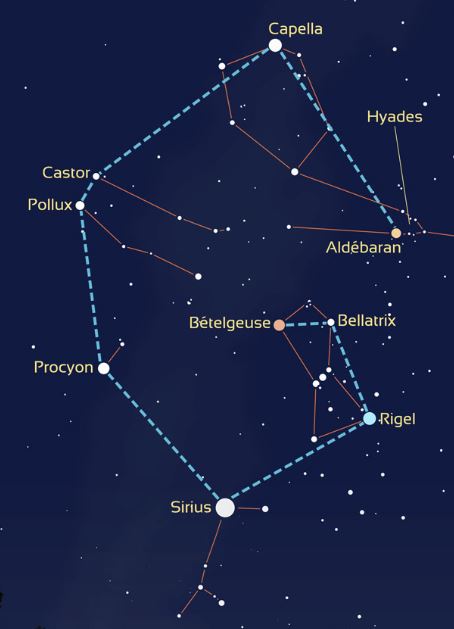
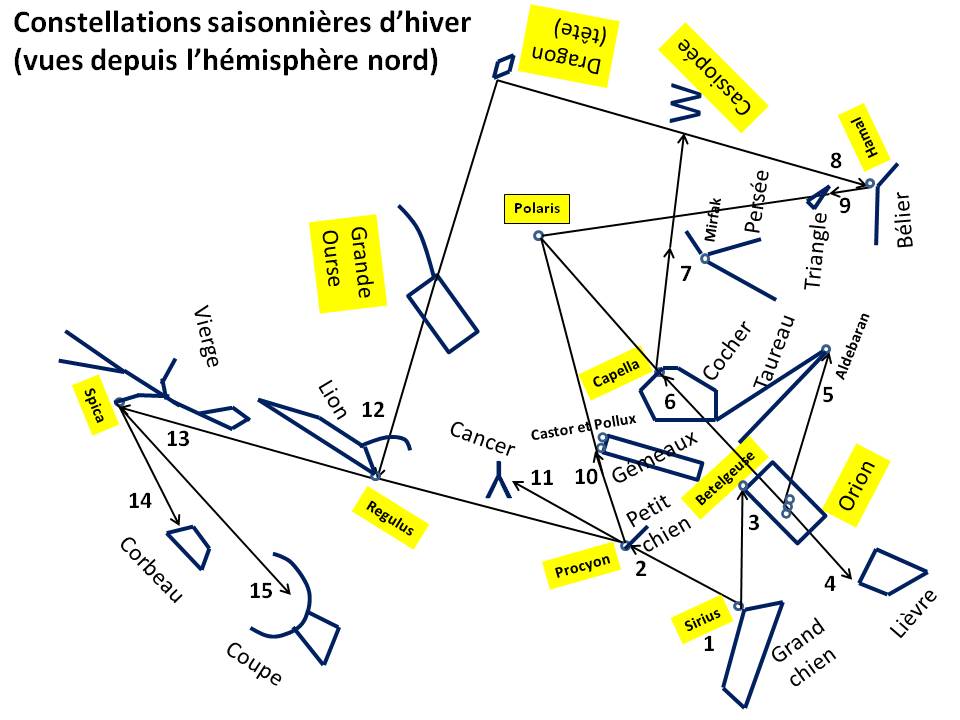
|
Synthesis : To find these constellations in the winter sky, the simplest method is the following [CHA][PER], by referring to the maps above : - Winter triangle and Winter hexagon. - Map of February 14, 2025 at 00:00 for mainland France or latitudes from 40 to 55°N, with zenith at the center of the portion of visible sky [STE]. - The "Big G". - Guide to locating winter seasonal constellations (in neutral representation). 0. Find the Winter Triangle located low above the southern horizon around midnight in winter (December to February) : Quasi-equilateral triangle, almost empty of stars, formed by three super-bright stars : Sirius (Canis Major), Procyon (Canis Minor) and Betelgeuse (Orion). The distance between each star is one width of an open hand. 1. Find the star Sirius, a brightest and lowest star in the Winter Triangle, blue-white in color. Find The Canis Major : Trapezoid of four bright stars (α, β, ε, δ) including Sirius (α) and extending the Polaris-Sirius line from Sirius (α). 2. Find the star Procyon, an easternmost star of the Winter Triangle (to the right of the line from Polaris to Sirius), white in color. Find The Canis Minor : Group of two bright stars (α, β) including Procyon (α) and turned towards this line. 3. Find the star Betelgeuse, a westernmost star of the Winter Triangle (to the left of the line from Polaris to Sirius), red in color. Find Orion : Large rectangle (α, γ, β, κ) including Betelgeuse (α) and crossed in its center by a belt of three aligned stars (ζ, ε, δ). Important note : This unusual method of spotting (first Sirius, which is unmissable, then Orion) seems more suitable for beginner observers than the classic reverse method (first Orion, then Sirius). 4. Find The Hare : Trapezoid of four bright stars (α, β, ε, μ), located near Orion's belt, on a line coming from Polaris and passing through Orion's belt. 5. Find the star Aldebaran, a super-bright orange star located near Orion, on a line coming from Sirius and passing through Betelgeuse, one open hand width apart from Betelgeuse. Find The Bull : Large V with eleven bright stars, including Aldebaran (α), the eye of the Bull, located very close to the base of the V. 6. Find the star Capella, a super-bright yellow star located halfway between Orion's belt and Polaris. Find The Charioteer : Hexagon of six bright stars (α, β, θ, γ, ι, ε) including Capella (α), touching Taurus and turned towards Orion. 7. Find the star Mirfak, a super-bright white star located halfway between Capella and Cassiopeia. Find Perseus : Large Y with three branches (α-β, α-γ and α-δ-ε-ζ) centered on Mirfak (α). 8. Find the star Hamal, a bright star located opposite Dragon's head from Cassiopeia. Find The Ram : Broken line of three bright stars (β, α, 41), including Hamal (α). 9. Find the Triangle : Elongated triangle of three bright stars, located near Hamal between Hamal and Polaris. 10. Find the stars Castor and Pollux, two super-bright close stars (Castor, white, and Pollux, orange), located near Procyon between Procyon and Polaris. Find The Twins : Group of eleven bright stars including Castor (α) and Pollux (β), forming a large elongated rectangle (α, β, γ, μ) turned towards Orion. 11. Find The Crab : Large Y with four bright stars, located opposite Sirius from Procyon. 12. Find the star Regulus, a super-bright blue star, located to the left of the line coming from Sirius and passing through Procyon, two open hand widths apart from Procyon, and also located opposite the Dragon's head from the center of the Great Bear (attachment point of the dipper handle). Find The lion : Group of nine bright stars forming a flattened trapezoid of four stars (α, β, δ, γ) including Regulus (α) and extended by a head (ε) and a mane (ε, μ, ζ, γ). 13. Find the star Spica, a super-bright blue star located low in the sky, on a line coming from Sirius and passing through Procyon, five open hand widths apart from Procyon. Find The Virgin : Group of nine bright stars, including Spica (α). 14. Find The Crow : Polygon of five stars including four bright ones (β, δ, γ, ε), located low in the sky, west of Spica (to the left of the line from Sirius to Spica), one open hand width apart from Spica. 15. Find The Cup : Polygon of four stars, including one bright star (δ), located low in the sky, west of Spica (to the left of the line from Sirius to Spica), two open hand widths apart from Spica. Notice the Winter Hexagon near the zenith around midnight in winter (December to February) : Symmetrical hexagon with six super-bright stars : Sirius (Canis Major), Procyon (Canis Minor), Pollux (The Twins), Capella (The Charioteer), Aldebaran (The Bull), Rigel (Orion). Notice the "Big G" near the zenith around midnight in winter (December to February) : Big G with nine super-bright stars : Betelgeuse, Bellatrix and Rigel (Orion), Sirius (Canis Major), Procyon (Canis Minor), Pollux and Castor (The Twins), Capella (The Charioteer), Aldebaran (The Bull). |
C4.6. Other constellations :
Other constellations are the following :
12 constellations that are difficult to see with the naked eye :
* Constellations too close to the horizon :
- The Dove (Columba, Col)
- The River (Eridanus, Eri)
- The Southern Fish (Piscis Austrinus, PsA)
- The Water Snake (Hydra, Hya)
* Constellations too faint in brightness (no star with a magnitude less than 4.0) :
- The Berenices's Hair (Coma Berenices, Com)
- The Little Fox (Vulpecula, Vul)
- The Lesser Lion (Leo Minor, LMi)
- The Lizard (Lacerta, Lac)
- The Sextant (Sextans, Sex)
* Constellations drowned in star-dense regions :
- The Hunting Dogs (Canes Venatici, CVn)
- The Little Horse (Equuleus, Equ)
- The Unicorn (Monoceros, Mon)
34 constellations not visible from Metropolitan France :
- The Air Pump (Antlia, Ant)
- The Altar (Ara, Ara)
- The Bird of Paradise (Apus, Aps)
- The Centaur (Centaurus, Cen)
- The Chameleon (Chamaeleon, Cha)
- The Chisel (Caelum, Cae)
- The Clock (Horologium, Hor)
- The Compass (Pyxis, Pyx)
- The Crane (Grus, Gru)
- The Drafting Compass (Circinus, Cir)
- The Fly (Musca, Mus)
- The Flying Fish (Volans, Vol)
- The Furnace (Fornax, For)
- The Goldfish (Dorado, Dor)
- The Indian (Indus, Ind)
- The Keel (Carina, Car)
- The Male Water Snake (Hydrus, Hyi)
- The Microscope (Microscopium, Mic)
- The Octant (Octans, Oct)
- The Painter (Pictor, Pic)
- The Peacock (Pavo, Pav)
- The Phoenix (Phoenix, Phe)
- The Reticle (Reticulum, Ret)
- The Sails (Vela, Vel)
- The Sculptor (Sculptor, Scl)
- The Southern Cross (Crux, Cru)
- The Southern Crown (Corona Australis, CrA)
- The Southern Triangle (Triangulum Australe, TrA)
- The Square (Norma, Nor)
- The Stern (Puppis, Pup)
- The Table Mountain (Mensa, Men)
- The Telescope (Telescopium, Tel)
- The Toucan (Tucana, Tuc)
- The Wolf (Lupus, Lup)
C4.7. Zodiacal constellations :
The astronomical zodiac is a band in the sky that extends about 8° on either side of the ecliptic.
It includes thirteen official constellations, which are the only ones that the Sun obscures during its annual path, as seen from Earth.
The astrological zodiac takes the names and the succession of the constellations of the astronomical zodiac, but is limited to twelve signs excluding Ophiuchus, in order to symbolically divide the ecliptic into twelve equal parts.
The vernal point (spring equinox) once marked the Sun's entry into the constellation of Aries, which justified its status as the first sign of the zodiac. But today, due to the precession of the equinoxes, this point is located in the constellation of Fishes.
The constellations of zodiac are as follows, listed in the order in which the Sun passes through them :
Their visibility from the northern hemisphere is as follows :
* Constellations visible all year round : none.
* Summer seasonal constellations (May to October) : The Scales, The Scorpion, Ophiuchus, Sagittarius, The Sea Goat, The Water Bearer, The Fishes.
* Winter seasonal constellations (November to April) : The Ram, The Bull, The Twins, The Crab, The Lion, The Virgin.
C4.8.
Tips for good observation :
To properly observe the stars, constellations, planets and satellites in the sky, it is advisable to [CHA][PER] :
C4.9. Coordinates, color and magnitude of a celestial body :
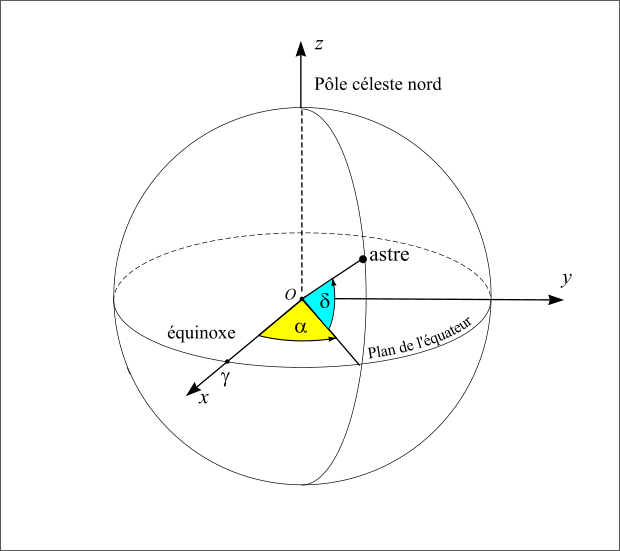
The coordinates of a celestial body are generally the equatorial coordinates (α and δ) defined as follows (see Figure above) :
- Celestial sphere : Imaginary sphere of infinite radius, centered on the Earth, onto which all celestial bodies observed from Earth are projected.
- Celestial equator : Imaginary great circle drawn on the celestial sphere, corresponding to the projection of the Earth's equator onto this sphere.
- Vernal point (γ) : Point of intersection of the celestial equator and the ecliptic at the time of the vernal equinox in the northern hemisphere.
- Right ascension (α) : Hour angle measured along the celestial equator, eastward from the vernal point, between the meridian passing through this point and the meridian passing through the celestial body. It is expressed in hours, from 0 to 24 h, with the following correspondence: 1 h = 15°. Right ascension is the celestial analog of terrestrial longitude.
- Declination (δ) : Angle measuring the distance of a celestial body from the celestial equator. It is expressed in degrees, from -90° (south celestial pole) to +90° (north celestial pole). Declination is the celestial analog of terrestrial latitude.
Example for the star Vega [IAU2] : α = 18 h 36 min 56.345 s (or 279.234735°), δ = +38° 47' 01.28" (or +38.783689°).
The angular distance (d) separating two celestial bodies in the sky, measured from Earth, is given by the following spherical trigonometry formula :
cos(d) = sin(δ1) sin(δ2) + cos(δ1) cos(δ2) cos(α1 - α2)
where α1 and α2 are the right ascensions of the two celestial bodies, δ1 and δ2 their declinations.
The apparent color of celestial bodies (seen with the naked eye) depends mainly on their surface temperature according to the following simplified classification :
- Blue : Very hot celestial bodies ( > 10 000 K approximately), such as Spica.
- White : Hot celestial bodies (from 6 000 to 10 000 K approximately), such as Sirius.
-
Yellow : celestial bodies of average temperature (from 5 200 to 6 000 K approximately), such as the Sun.
- Orange : Cold celestial bodies (from 3 700 to 5 200 K approximately), such as Aldebaran.
- Red : Very cold celestial bodies ( < 3 700 K approximately), such as Betelgeuse.
However, factors significantly influence the apparent color :
- Brightness (whitish effect for very bright celestial bodies)
-
Earth's atmosphere (reddish effect near the horizon due to the light diffusion in the air)
-
Interstellar dust (accentuation of red by absorption of short wavelengths (blue))
- Interstellar gas clouds (absorption and diffusion of certain wavelengths depending on their composition)
- Sensitivity of the human eye (attenuation of blue and red in the dark)
Warning : Contrary to popular belief (red = hot, and blue = cold), the further you go from red to blue, the higher the star surface temperature.
The apparent magnitude (M) of a celestial body corresponds to its brightness state as perceived from Earth :
M = -2.5 log10[F/F0]
with :
F = luminous flux received from the celestial body (in W/m2)
F0 = reference luminous flux corresponding to M = 0 (historically that of Vega, before the current more precise measurements).
M is a standardized measure that takes into account four factors :
- Intrinsic luminosity of the celestial body. It corresponds to the total power of light (L in Watt) emitted at its surface, then diffused uniformly in all directions across a spherical surface of increasing radius r.
- Distance between the celestial body and the Earth. The apparent luminosity (I in W/m2), perceived at the distance r from the celestial body, decreases in fact according to the inverse square law : I = L/(4 π r2).
- Extinction (absorption and diffusion of light by the Earth's atmosphere, interstellar dust and gas clouds between the celestial body and the Earth)
- Sensitivity of the human eye (which perceives the apparent luminosity according to an inverse logarithmic scale)
Warning : The lower the numerical value (M) of the apparent magnitude, the brighter the celestial body.
C4.10. Sources relative to constellations :
[CHA] ChatGPT, le moteur d'Intelligence Artificielle développé par OpenAI.
[DAR] Découvrir le ciel à l'oeil nu, Bertrand D'Armagnac et Carine Souplet, Stelvision.
[IAU1] IAU, Les constellations.
[IAU2] IAU, Comment sont nommées les étoiles ? or Current List of IAU Star Names.
[IMA] Imago Mundi, Les 88 constellations.
[IST] iStock, Constellations.
[LES] Les Astronautes, Comment reconnaître les constellations dans le ciel ?.
[PER] Perplexity, le moteur d'Intelligence Artificielle développé par Perplexity AI.
[STE] Stelvision, Carte du ciel du jour (pour France métropolitaine ou latitudes de 40 à 55°N, avec zénith au centre de la portion de ciel visible).

The Moon exerts a subtle but real influence on life on Earth. Through its cycles and gravitational pull, it regulates the tides, guides certain animal behaviors, and appears to affect plant growth. In humans, its effects are more difficult to demonstrate with certainty.
C8.1. The Moon's influence on animals :
In animals, the Moon influences their behavior primarily through the increased brightness of a full moon. This nighttime light notably alters hunting and reproductive cycles.
Predators such as cats and owls hunt more effectively thanks to the enhanced light, while prey like rodents and insects reduce their movements to minimize the risk of being detected.
In the marine environment, many species synchronize their reproduction with lunar cycles, influenced by both light intensity and tides.
Domestic animals are sometimes more restless on full moon nights, likely due to this unusual brightness.
C8.2. The Moon's influence on humans :
In humans, the Moon's influence on sleep, mood, births, and behavior is the subject of studies that are often contradictory or inconclusive.
However, the perceived effect of the Moon could stem from a psychological phenomenon : people tend to remember unusual events more readily when they coincide with a full moon, while forgetting periods without any notable events.
C8.3. The Moon's influence on plants :
The Moon's influence on plant growth has always been a subject of lively debate between scientists and biodynamic practitioners.
According to the biodynamic approach, inherited from the work of Rudolf Steiner, solar and lunar cycles, as well as other cosmic rhythms, are the expression of cosmic forces including the Moon, the Sun, and the planets. Sap rises in plants during the waxing moon, which promotes the growth of aerial parts such as leaves and flowers, a favorable period for sowing and harvesting. Conversely, sap descends towards the roots during the waning moon, a favorable period for pruning, dividing, taking cuttings, and harvesting root vegetables.
Biodynamic practitioners also believe that the Moon's position relative to the zodiacal constellations has a specific influence on plant growth. For example, when the Moon is in front of the constellation Virgo (earth element), this period is said to particularly favor root growth, while in Libra (air element), it is thought to favor flower growth.
Conversely, according to the scientific approach, the influence of the lunar phase on plant growth has never been established in a robust, clear, and reproducible manner.
While lunar gravitational forces explain Earth's large ocean tides, they are too weak to have a significant effect on individual plants.
Furthermore, the intensity of moonlight, resulting from the reflection of solar radiation, is insufficient to influence photosynthesis and other essential biological processes.
On the other hand, it is proven that biodynamic practices have beneficial effects on soil quality and biodiversity, but these effects are attributed primarily to agricultural practices and not to the direct influences of lunar or cosmic forces claimed by biodynamics.
Thus, According to modern science, even if a lunar influence exists, it is marginal compared to other agronomic factors that influence crop management.
The key conditions for success, recognized and validated by agronomic research, are primarily linked to the following fundamental factors :
1. Quality of plant propagation material (seeds, seedlings, bulbs, cuttings) :
- Material from reliable sources (healthy and vigorous, free from diseases and pests)
- Variety adapted to the local climate, soil pH, and exposure (sunny or shaded)
2. Soil type :
- Soil drainage to prevent waterlogging around roots
- Soil enrichment with humus (manure, compost) and minerals (lime, sand, clay)
- Crop rotation to prevent disease and soil depletion
- Tilling without disturbing the soil structure to maintain its biological activity
3. Protection against climatic hazards :
- Windbreaks (hedges, nets, tunnels, greenhouses)
- Frost protection (winter fleece, thick mulch, cloches)
- Drought protection (organic mulch, appropriate watering)
4. Agricultural practices :
- Respect for planting depth and Plant spacing
- Watering at the right time and without overwatering
- Regular weeding
- Mulching to retain moisture and limit weeds
- Enriching the plant with fertilizer (nitrogen, phosphate, potassium)
- Monitoring and phytosanitary treatment
5. Planting periods :
- Season suited to each variety
- Taking into account the upcoming weather conditions
- Lunar phase, whose influence, if any, remains very marginal compared to other influences
C8.4. The dictons :
Listed below are the main sayings with a known scientific explanation.
Moon and Tides :
- The Moon rules the tides,
- When the Moon smiles, the water smiles too : The tides are directly caused by the gravitational pull of the Moon (and the Sun). And when the Moon is full or new, the Earth, Moon, and Sun are aligned (spring tides).
Moon and Animals :
- A full moon makes dogs howl and roosters stay awake,
- When the Moon is full, animals are in distress,
- A bright moon makes wolves angry,
- When the Moon is round, dogs howl at its crescent,
- A red moon makes animals and plants suffer : Nocturnal animals (wolves, dogs, birds) react to the light.
Moon and Humans :
- He who sleeps during the full moon dreams of misfortune,
- Full moon keeps everyone awake
,
- Children sleep poorly during the full moon,
- Bright moon makes the heart alert : Some people sleep less deeply and for shorter periods during the full moon.
- Bright moon, prosperous love : Moonlight stimulates nighttime activity and social outings.
Moon and Plants :
- Waxing moon, rising sap,
- When the moon is waxing, everything grows,
- Waning moon, growing roots,
- When the moon is waning, everything shrinks : Lunar phases whose influence, if it exists, remains very marginal compared to other influences.
- Red moon, nothing grows,
- Red moon burns young shoots,
- Red moon makes animals and seedlings suffer : The period after Easter during which clear nights lead to heat loss through radiation, making frost possible.
Moon and Weather :
See Weather - The dictons
See detail.


Purchasing an electric car, whether 100 % electric, hybrid or hydrogen, requires careful consideration.
These different types of vehicles have the following advantages and disadvantages compared to a conventional car with a thermal engine (petrol or diesel).
D3.1. The 100 % electric car
D3.2. The hybrid car
D3.3. The hydrogen car
D3.4. Synthesis :
|
Statistics : At the end of 2024, the French electric passenger car fleet (excluding light commercial vehicles) represents approximately 8 % of the total fleet, broken down as follows : 2.2 % (100 % electric), 1.5 % (plug-in hybrids) and 4.4 % (non-rechargeable hybrids). Purchasing a 100 % electric or hybrid vehicle : Many buyers focus on the purchase price, short-term fuel savings, and tax or environmental benefits. But you also need to consider : - Costs beyond 8 years, including possible battery replacement. - Underestimated expenses, such as as additional costs (insurance, tire replacement, repairs, software updates) and cost of recharging the battery, particularly at fast charging stations. - The financial risk that a minor accident could damage the battery (for example, a simple collision with a sidewalk) and result in the vehicle being classified as a wreck (damage to the electrical system, impact on sensitive areas of electric vehicles, total or partial immersion in water). - The concerns about the autonomy of the 100 % electric car and the network of charging stations. - The few mechanics authorized to work on electric and hybrid vehicles. For low-income households, two major obstacles remain : the high purchase price and the risk of being classified as a wreck after even a minor collision. Thus, the appeal of a 100 % electric or hybrid car is based more on environmental concerns, particularly the reduction of CO2 emissions, than on strictly short- or long-term economic logic. An informed decision therefore requires a complete analysis of all these aspects in order to allow buyers to make an objective choice adapted to their situation. Note that electric cars with higher ground clearance, such as electric SUVs or crossovers, offer better protection against the two major risks for electric vehicles : underbody impact and accidental immersion. Purchasing a hydrogen vehicle : Purchasing a hydrogen vehicle is now more relevant for professional fleets than for individuals due to a market that is still developing. The main obstacles include : - a high purchase price, - an insufficient network of hydrogen refueling stations, - as for electric or hybrid cars, the financial risk that a accident could damage the battery, or even the hydrogen tank or fuel cell, and result in the vehicle being classified as a wreck. European regulation : From 2035, by European regulation published in the EU Official Journal on 25 April 2023 and entered into force on 15 May 2023 [EUR] : - The sale of new cars with combustion engines (petrol, diesel and current hybrids), such as passenger cars or light commercial vehicles, will be banned in the European Union. Only "zero-emission" vehicles, such as 100 % electric cars or those using synthetic fuels (e-fuels) or hydrogen (FCEV), will be allowed to be sold. - The ban does not apply to the second-hand market. - Combustion-engine cars already in circulation are not affected and may continue to be used and resold. The hybrid car market, despite its current success, is therefore set to gradually disappear by 2035, unless they achieve exceptional performance in electric mode. The hybrid car thus appears to be a simple transitional stage towards all-electric. First aid : The additional actions to take on an accident-damaged electric, hybrid or hydrogen vehicle are as follows : - Identify and report the type of vehicle to the emergency services because these vehicles present specific risks, particularly concerning the high-voltage battery, the high-pressure hydrogen tank and fire management. - Maintain a safety distance of at least 30 metres around the accident-damaged vehicle to avoid any danger of electric shock, explosion or fire. - Do not use water to extinguish a battery fire without the advice of the fire department. In the rare event of a lithium-metal battery fire, the use of water may make the fire worse. |
D3.5. Sources relative to electric cars :
[ADE] ADEME, Mondial de l'automobile : l'ADEME publie son avis sur le véhicule électrique : une batterie de taille raisonnable assure une pertinence climatique et économique.
[AUJ1] L'auto-journal, Voitures électriques : quel est le coût des réparations ?.
[AUJ2] L'auto-journal, Véhicules électriques et entretiens : un vrai cauchemar ?.
[AUM] L'Automobile Magazine, Les voitures électriques sont-elles 3 fois plus dangereuses pour les piétons ?.
[AUT] Auto, Attention, les voleurs s'attaquent aux batteries des véhicules hybrides.
[CAP1] Capital, Accidents de la route : dans quels cas votre voiture est-elle jugée irréparable ?.
[CAP2] Capital, Automobile : découvrez pourquoi réparer un véhicule électrique coûte plus cher !.
[CEN] La Centrale, Quand la batterie flanche : dites adieu à votre voiture électrique et direction la casse !.
[CHA] ChatGPT, le moteur d'Intelligence Artificielle développé par OpenAI.
[CNR] CNRS Le journal, Les défis de la voiture à hydrogène.
[ECO] Ecoconso, Voiture électrique : ses avantages et inconvénients.
[EDM] Les éditions du moteur, Voiture électrique : Le désamour inattendu qui touche 30 % des propriétaires.
[EUR] EUR-Lex, Règlement (UE) 2023/851 du Parlement européen et du Conseil du 19 avril 2023 modifiant le règlement (UE) 2019/631 en ce qui concerne le renforcement des normes de performance en matière d'émissions de CO2 pour les voitures particulières neuves et les véhicules utilitaires légers neufs conformément à l'ambition accrue de l'Union en matière de climat.
[MAC] Machines Production, Voitures électriques : l'épineux problème des batteries après un accident.
[NUM] Numerama, Au moindre accident votre voiture électrique peut finir au rebut à cause de sa batterie.
[PER] Perplexity, le moteur d'Intelligence Artificielle développé par Perplexity AI.
[PRE] Pressecitron, Une voiture électrique coûte-t-elle vraiment moins cher à l'usage qu'une thermique ?.
[QUE] Que choisir, Comment choisir une voiture hybride.

D7.1. Introduction :
Quantum physics is a fundamental branch of physics that describes the universe at the microscopic level of atoms, molecules, and elementary particles, taking into account their dual nature of wave and particle.
It differs from classical physics in its counterintuitive concepts such as energy quantization, wave-particle duality, superposition of states, quantum indeterminism, and quantum nonlocality.
These concepts have given rise to many modern technologies such as electronics, quantum computers, medical imaging, and nanotechnology.
Albert Einstein played a major role in the development of quantum physics, notably through his explanation of the photoelectric effect (1905), the quantization of atomic oscillators (1907), wave-particle duality for light (1909), stimulated emission (1917) and the EPR paradox (1935).
Although he always recognized the validity and effectiveness of quantum formalism, he opposed the probabilistic interpretation of Niels Bohr and the Copenhagen School. Einstein defended a simultaneously deterministic and local view of the quantum world, believing in the existence of "hidden variables" that could explain quantum phenomena more completely.
However, subsequent experiments, notably those of Alain Aspect in 1982 [ASP], contradicted this view by demonstrating that quantum mechanics violates quantum locality regardless of whether it is deterministic or not.
Quantum mechanics constitutes the theoretical and mathematical foundation which formalizes the fundamental principles governing quantum physics.
D7.2. Standard model of particles physics (reminder) :
See Relativity - Lexicon : Standard model of particles physics.
D7.3. Fundamental principles :
The fundamental principles governing quantum physics are as follows [CHA][PER], listed in chronological order of discovery.
1. Quantization of Energy (Max Planck, 1900, Albert Einstein, 1905-1917)
Energy can only take discrete values, called quanta, and not continuous values.
This principle was gradually established and extended as follows :
- Blackbody radiation (Max Planck, 1900, and Nobel Prize in Physics in 1918) : For an atom, the energy difference E between two energy levels is given by : ΔE = h ν, where h is Planck's constant and ν is the frequency associated with the transition.
- Photoelectric effect (Albert Einstein, 1905, and Nobel Prize in Physics in 1921) : Einstein extends Planck's quantization to light itself.
- Quantization of atomic oscillators (Albert Einstein, 1907) : Einstein applies quantization to the vibrations of atoms in a solid.
- Stimulated emission (Albert Einstein, 1917) : Einstein completes the description of the interaction between light and matter in which an incident photon causes an atom to de-excite, emitting a second photon of the same direction, frequency, and polarization.
Confirmation of the quantization introduced by Planck (1900) : Franck and Hertz's experiment (1914) showed that accelerated electrons lost energy in discrete amounts during collisions with mercury atoms.
2. Wave-Particle Duality (Albert Einstein, 1909, Louis de Broglie, 1924)
Quantum objects, such as electrons and photons, exhibit both particle and wave properties depending on the experimental conditions.
The wavelength λ associated with a particle with momentum p is given by : λ = h/p
For a non-relativistic particle with mass m and velocity v, we have: p = m v.
For a photon with energy E, we have : p = E/c
This principle was established in two steps as follows :
- Einstein lays the foundations of wave-particle duality for light (1909).
- De Broglie generalizes this concept to all matter (1924, and Nobel Prize in Physics in 1929).
Confirmation : Davisson-Germer's experiment (1927) demonstrated the diffraction of electrons by a nickel crystal, thus confirming their wave nature.
3. Statistics of Bosons and Fermions (Satyendra Nath Bose and Albert Einstein, 1924, Enrico Fermi and Paul Dirac, 1926)
Bosons (with integer spin, like the photon) follow Bose-Einstein statistics for their collective behavior.
Fermions (with half-integer spin, like the electron) follow Fermi-Dirac statistics for their collective behavior.
Confirmations :
- Bose-Einstein condensate (Eric Cornell and Carl Wieman, 1995, and Nobel Prize in Physics in 2001) by cooling rubidium atoms (bosons).
- Pauli blockade (MIT, 2021) by cooling a lithium-6 gas cloud (fermions).
4. Pauli Exclusion (Wolfgang Pauli, 1925, and Nobel Prize in Physics in 1945)
Two identical fermions, like electrons, protons, or neutrons, cannot simultaneously occupy the same quantum state in the same system.
This principle is fundamental to explaining the electronic structure of atoms, particularly the distribution of electrons in atomic shells and subshells, which leads to the structure of the periodic table of elements.
Confirmations :
- Analysis of the Zeeman effect (1927-1930).
- Study of electronic band structure and nuclear physics (1930-1940).
5. Quantum Superposition (collective, 1926)
A quantum system exists in an indeterminate global state as a superposition of several states simultaneously until a measurement is made. After the measurement, the system collapses into a single state corresponding to the observed result.
Confirmation : Clinton Davisson and Lester Germer's experiment (1927) on the diffraction of electrons by a crystal.
|
Formalization [PER][CHA] :
It applies to any quantum phenomenon, such as the Stern-Gerlach experiment (see below) for the discrete case and the calculation using the continuous Schrödinger method in the continuous case. The wave function Ψ(x, t)is an abstract representation containing all possible information about the state of a particle or quantum system at a given instant. It allows us to calculate the probabilities of different measurement outcomes but does not determine with certainty the outcome of a single measurement. It is expressed mathematically in a standard way as the superposition of eigenstates Ψj in the form : - Discrete case : Ψ(x, t) = ∑j [cj Ψj(x, t)] where j is the index that numbers the different eigenstates Ψj - Continuous case : Ψ(x, t) = ∫R [c(k) Ψk(x, t) dk] where k is a continuous variable. where the variable x can be a position, a volume, a momentum, an energy, etc. Given the normalization condition (see below), the unit of Ψ(x, t) is dimensionless in the discrete case and the square root of the inverse of the unit of x in the continuous case (for example, Ψ(x,t) has the unit of m-1/2 for x expressed in meters). The eigenstates Ψj are characteristic modes of the system for which the measurement of an observable always gives the same result with a probability of 100 %. These modes are analogous to : - Discrete case : the specific tuning frequencies of a radio, where the observable is the radio frequency, - Continuous case : the specific vibration modes of a taut string, where the observable is the vibration frequency. Each eigenstate Ψj(x, t) is expressed in the complex form : Ψj(x) e-i Ej t/h' with a non-temporal part Ψj(x) that is a solution to the stationary Schrödinger equation and a phase part that depends on time t. Ej is the energy associated with the eigenstate Ψj and h' is the reduced Planck constant. The coefficients cj are the probability amplitudes associated with each eigenstate. They are expressed in the complex form : |cj| ei θj where |cj| is the module of coefficient and θj is the initial phase angle in the complex plane. The determination of the cj coefficients is essentially experimental. The |cj| moduli are obtained by statistical measurements on many copies of the system. Relative phases require more advanced techniques such as quantum tomography. More generally, regardless of the type of quantum state (eigenstate or superimposed), the probability amplitude is a complex coefficient associated with each eigenstate of the wave function, allowing the calculation of the probability of observing a specific outcome during a measurement. This concept was introduced in 1926 by Max Born [BOU], who showed that the wave function Ψ could not be interpreted directly as a probability because this would violate the rules for calculating probability for compound events. He proposed that the probability of observing a given state be given by the square of the modulus of the probability amplitude, i.e. |Ψ|2 Hence the following four cases : 1. Discrete case of an eigenstate Ψj : The state of the system is Ψj, with a probability amplitude of 1 for Ψj and a probability of 1 of observing state Ψj 2. Continuous case of an eigenstate Ψj : The state of the system is Ψj(x, t), with a probability amplitude Ψj(x, t) and a probability density ρ(x, t) = |Ψj(x, t)|2 giving the probability of finding at time t the value x of the measured variable. 3. Discrete case of a superposition of eigenstates : The state of the system is a superposition Ψ(x, t) = ∑j cj Ψj(x, t), with a probability amplitude cj for each eigenstate Ψj and a probability Pj = |cj|2 of observing state Ψj 4. Continuous case of a superposition of eigenstates : The state of the system is a superposition Ψ(x, t) = ∫R c(k) Ψk(x, t) dk, with a probability amplitude density c(k) for each eigenstate Ψk and a probability density ρ(x, t) = |Ψ(x, t)|2 giving the probability of finding at time t the value x of the measured variable taking into account the effects of quantum interference between the different eigenstates. Note that the probability amplitude is the wave function itself only in the continuous case of an eigenstate (case 2). The normalization condition guaranteeing that the sum of the probabilities is equal to 1 also imposes that : 1. Discrete case of an eigenstate Ψj : ∑i |Ψj(xi)|2 = 1 where xi are the discretization points. 2. Continuous case of an eigenstate Ψj : ∫R |Ψj(x, t)|2 dx = 1 3. Discrete case of a eigenstates superposition : ∑j |cj|2 = 1 4. Continuous case of a eigenstates superposition : ∫R |c(k)|2 dk = 1 or ∫R |Ψ(x, t)|2 dx = 1 Concrete example (Stern-Gerlach experiment, 1922) : The wave function of a silver atom whose spin is in a superposition of states along the z axis can be written : Ψ = c1 |+z> + c2 |-z> where the eigenstates |+z> and |-z> represent the "up" and "down" orientations of the spin along the z axis, respectively. These eigenstates are also the eigenvectors of the spin operator Sz which allows us to measure the projection of the angular momentum on the z axis. This operator is defined by the following matrix : Sz = h'/2 (1 0) (0 -1) where h' is the reduced Planck constant. The eigenvectors associated with this matrix are |+z> = (1, 0)T for the eigenvalue +h'/2 (spin "up"), and |-z> = (0, 1)T for the eigenvalue -h'/2 (spin "down"). These eigenvalues represent the quantization of the angular momentum projections on the z axis, expressed in units of h' The complex coefficients c1 = 1/(21/2) and c2 = i/(21/2) are the probability amplitudes, taking into account both the moduli and the relative phase between the two eigenstates. Therefore, if we perform a spin measurement on the z axis, there is a 50 % chance (= |c1|2) of obtaining the value + h'/2 ("up" state) and a 50 % chance (= |c2|2) of obtaining the value -h'/2 ("down" state). |
6. Quantum Indeterminism (Max Born, 1926, and Nobel Prize in Physics in 1954)
Measurement results are not deterministic, but probabilistic, when the system evolves freely between measurements or is reset to its initial state before each new experiment.
On the other hand, repeated measurements under the same experimental conditions, at very short intervals, give the same result because the system remains in the measured state after the first observation.
Confirmation : Repeated experiments on Young's slits.
Interpretations :
- In the Copenhagen interpretation (Bohr, Heisenberg), this principle calls into question the idea that the properties of a quantum system have an objective reality independent of measurement.
- But other interpretations, such as the de Broglie-Bohm (hidden variable theory) or the Everett (many-worlds) interpretation, challenge this idea while remaining compatible with experimental predictions. To this end, the de Broglie-Bohm interpretation preserves determinism while accepting the principle of quantum nonlocality, and the Everett interpretation avoids the nonlocality problem by proposing that all possible outcomes of a measurement occur simultaneously in distinct universe branches.
7. Quantum Uncertainty (Werner Heisenberg, 1927, and Nobel Prize in Physics in 1932)
There is a fundamental limit to the precision with which certain pairs of physical quantities can be measured, including position and momentum, energy and time, spin and orientation.
For example, the relationship between the uncertainties between position (x) and momentum (p) is given by :
Δx Δp ≥ h'/2
where h' is the reduced Planck constant.
Indirect confirmation : Davisson-Germer's (1927) experiment on electron diffraction by a nickel crystal.
8. Tunneling Effect (George Gamow, 1928)
A particle can penetrate an energy barrier even without the classically required energy. The particle's wave function does not vanish at the barrier but attenuates within it, allowing a non-zero probability of crossing it.
Confirmation : George Gamow's experiment (1928) on the alpha decay of radioactive nuclei.
9. Quantum Entanglement (EPR paradox, by Albert Einstein, Boris Podolsky, Nathan Rosen, 1935)
Two particles are said to be entangled when they form a global quantum system such that measuring the state of one instantly determines the state of the other, regardless of the distance between them.
These instantaneous quantum correlations do not constitute signal transmission, thus escaping the framework of relativistic causality without contradicting it.
Confirmation : Experiments by Alain Aspect (1982, and 2022 Nobel Prize in Physics) that confirmed the predictions of quantum mechanics in violation of Bell's inequalities, thus confirming quantum entanglement [ASP].
10. Path Integral (Richard Feynman, 1948)
A particle traveling from one point to another simultaneously follows all possible paths to reach its destination. Each path is associated with a complex amplitude (modulus and phase), and the probability of finding the particle at a given location is determined by the sum of the amplitudes (with their phases) of all possible trajectories.
This approach is an elegant and powerful reformulation of the Schrödinger equation.
Confirmation : Hitachi's (1989) experiment on single electron interference.
11. Quantum Decoherence (David Bohm, 1951)
A quantum system can lose its coherence (superposition of states) by interacting with its environment, leading to seemingly classical behavior.
Confirmation : Experiments demonstrating the quantum-classical transition (Serge Haroche, 1996, Anton Zeilinger, 2003).
12. Quantum nonlocality (Bell's theorem, by John Bell, 1964)
Quantum objects can exhibit instantaneous correlations over distance. Nonlocality encompasses quantum entanglement by including correlations over time, complex multi-particle systems, interactions between particles and macroscopic objects, and delocalized phenomena without requiring direct interaction.
Confirmation : Experiments by Alain Aspect (1982) confirmed the predictions of quantum mechanics in violation of Bell's inequalities, thus confirming nonlocality [ASP].
13. Quantum Field Theory (collective)
Quantum field theory (QFT) is a theoretical framework unifying quantum mechanics and restricted relativity. It models particles as localized excitations of quantum fields that fill all of space-time, making it possible to explain the creation and annihilation of particles.
Only quantum entanglement escapes the interpretation of causality by its non-local character and the absence of signal transmission, while remaining compatible with the formalism of restricted relativity.
The following contributions are worth mentioning :
- Quantum theory of the electromagnetic field (Paul Dirac, 1927), confirmed in 1930 by the analysis of atomic spectra (notably Alfred Lande and Otto Stern).
- Quantum electrodynamics (QED), describing the interaction between light and matter (Richard Feynman, Julian Schwinger, Sin-Itiro Tomonaga, Freeman Dyson, 1940, and Nobel Prize in Physics in 1965), confirmed in 1947 by Polykarp Kusch and Henry Foley through experiments on the electron's magnetic moment.
- Non-Abelian gauge theories (Yang Chen-Ning and Robert Mills, 1954), providing a theoretical framework for describing non-Abelian interactions such as the weak and strong forces.
- Unification of electromagnetism and the weak force in a standard model (Steven Weinberg, Abdus Salam, Sheldon Glashow, 1960, and Nobel Prize in Physics in 1979), confirmed in 1983 at CERN by the discovery of the W+, W-, and Z0 bosons.
- Higgs boson (Peter Higgs and François Englert, 1964, and Nobel Prize in Physics in 2013) confirmed in 2012 at CERN by the ATLAS and CMS experiments at the LHC (Large Hadron Collider).
- Quantum chromodynamics (QCD), describing the strong interaction between quarks and gluons (David Gross, Frank Wilczek, David Politzer, 1973, and Nobel Prize in Physics in 2004, Kenneth G. Wilson, 1974), confirmed in 1979 at the DESY (Deutsches Elektron SYnchrotron) center by observing hadronic jets from high-energy particle collisions.
D7.4. Quantum state :
The quantum state of an elementary particle is a complete mathematical description of its observable and probabilistic aspects, distinct from its intrinsic properties.
It also extends to compound systems where interactions, correlations, and entanglement phenomena between particles play a fundamental role.
It is formalized by a state vector |ψ> in an abstract Hilbert space, associated with a wave function ψ(x,t) in a concrete basis, generally the position or momentum basis.
Intrinsic properties are invariant characteristics that define the fundamental nature of the particle, in particular the mass m and the intrinsic quantum numbers.
Observables are measurable physical quantities (such as position x or momentum p) represented mathematically by Hermitian operators (such as X or P).
- Before measurement, the observable is a statistical prediction obtained by calculating the weighted average of the possible outcomes of the measurement, the weights being determined by the probabilities associated with the initial quantum state of the system.
- After measurement, an observable provides a value that corresponds to one of the eigenvalues of the operator associated with the observable.
Operators act on the quantum state of the system (wave function or state vector in a Hilbert space) to calculate information, such as the possible values of observables (eigenvalues) and the probabilities associated with each measurement result. For example :
- the position operator X is the multiplication by x in the form : X(Ψ(x)) = x Ψ(x), allowing the calculation of the average value of the position for this state.
- the kinetic energy operator T acts on the wave function in the form : T(Ψ(x)) = -h'2/(2 m) (d2Ψ(x, t)/dx2)
- the momentum operator P acts by differentiation in the form : P(Ψ(x)) = -i h' dΨ(x)/dx, allowing the calculation of the average value of the momentum for this state.
Note that P can also be written : P = -i h' d/dx
- the Hamiltonian operator H acts on the wave function in the form : H(Ψ(x, t)) = -h'2/(2 m) (d2Ψ(x, t)/dx2) + V(x) Ψ(x, t), allowing the calculation of the total energy of the system.
Note that H can also be written : H = -h'2/(2 m) (d2/dx2) + V(X) = P2/(2 m) + V(X)
- The angular momentum operator J acts on the wave function in the form of a vector product : J(Ψ(x, t)) = r x P(Ψ(x, t)), where r is the position vector and P is the quantized motion operator, allowing the system's angular momentum to be calculated.
- The parity operator π acts on the wave function in the form : π(Ψ(x)) = Ψ(-x), allowing the symmetry of the wave function to be determined with respect to spatial inversion.
- The scaling operators (a+ creation and a annihilation) act on quantum states by adding or removing an excitation particle or quantum.
- The spin operator S acts on spin wave functions in the form of 2x2 Pauli matrices, allowing the intrinsic angular momentum of particles to be described. These matrices are as follows :
σ1 = σx =
(0 1)
(1 0)
σ2 = σy =
(0 -i)
(i 0)
σ3 = σz =
(1 0)
(0 -1)
These matrices verify the property : σ1 σ2 σ3 = i I where I is the Identity matrix.
The eigenvalue is a possible and specific outcome obtained when measuring an observable on a quantum system. It is obtained with certainty if the system is in a corresponding eigenstate, and with a given probability if the system is in a superposition of eigenstates. See Stern-Gerlach experiment.
The eigenvector represents the state of the system when the measurement of an observable yields an eigenvalue. See Stern-Gerlach experiment.
Eigenvectors form a basis for the space of quantum states, allowing all possible configurations of the system to be described.
Measurement probabilities describe how these observables are distributed across their possible value domains in terms of probability density.
They follow Born's rule according to which the probability density ρ is |<Ψj|Ψ>|2, where Ψj is the eigenstate associated with an eigenvalue of the measured observable, that is, the state the system is in immediately after the measurement.
The bra-ket notation <.|.> denotes the Hermitian scalar product which generalizes the classical scalar product to complex vector spaces in the form :
< u|v > = v+.u
where :
u and v = any two column vectors
v+ = adjoint of v = transposed complex conjugate such that v+ = (v*)T
* = complex conjugate operator without transposition
Example : if u = (1 + 2 i, 3)T and v = (4 + 5 i, 6 i)T, then v* = (4 - 5 i, -6 i)T, v+ = (v*)T = (4 - 5 i, -6 i) and < u|v > = v+.u = (4 - 5 i)(1 + 2 i) + (-6 i)(3) = 14 - 15 i
Examples of elementary particles with intrinsic/observable distinction :
Characteristics of the Electron e- :
| Classification : Lepton
| Composition : N/A (Elementary particle)
| Mass (m) = 0.511 MeV/c2
| Intrinsic magnetic moment (μ) = -9.284 10-24 J/T
| Chirality = Right and Left (mixing possible)
| CPT (Charge, Parity, Time) Symmetry : Yes
| Fundamental interactions : electromagnetic, weak and gravitational forces
| Lifetime (τ) = perfectly stable (6.6 1028 years)
| Anti-particle : positron
| Intrinsic quantum numbers :
| | Spin (S) = 1/2
| | Isospin (T3) = -1/2
(for weak isospin)
| | Electric charge (Q) = -1e
| | Color Charge : N/A (particle other than Quark and Gluon)
| | Flavor (Le) : electronic
| | Leptonic number (L) = +1
| | Baryonic number (B) = 0
| Observable quantum numbers :
| | Principal quantum number (n) = strictly positive integer
| | Secondary or azimuthal quantum number (l) = integer from 0 to n
- 1
| | Magnetic quantum number (ml) = integer from -l to +l
| | Magnetic spin quantum number or spin projection (ms) = +1/2 ("up") or -1/2 ("down")
| | Total angular momentum quantum number (j) = |l ± s|
| | Quantum number or projection of the total angular momentum (mj) = from -j to +j by integer steps
| | Projection of the magnetic moment (μz) = ±9,284 10-24 J/T
| | Parity (P) = accordind to contexte
| | Position, momentum and total energy
Characteristics of the Positron e+ = Anti-electron :
| Classification : Anti-Lepton
| Composition : N/A (Elementary particle)
| Mass (m) = 0.511 MeV/c2
| Intrinsic magnetic moment (μ) = +9.284 10-24 J/T
| Chirality = Right and Left (mixing possible)
| CPT (Charge, Parity, Time) Symmetry : Yes
| Fundamental interactions : electromagnetic, weak and gravitational forces
| Lifetime (τ) = perfectly stable in isolation and short in the presence of matter
| Anti-particle : electron
| Intrinsic quantum numbers :
| | Spin (S) = 1/2
| | Isospin (T3) = +1/2
(for weak isospin)
| | Electric charge (Q) = +1e
| | Color Charge : N/A (particle other than Quark and Gluon)
| | Flavor (Le) : electronic
| | Leptonic number (L) = -1
| | Baryonic number (B) = 0
| Observable quantum numbers :
| | Principal quantum number (n) = strictly positive integer
| | Secondary or azimuthal quantum number (l) = integer from 0 to n - 1
| | Magnetic quantum number (ml) = integer from -l to +l
| | Magnetic spin quantum number or spin projection (ms) = +1/2 ("up") or -1/2 ("down")
| | Total angular momentum quantum number (j) = |l ± s|
| | Quantum number or projection of the total angular momentum (mj) = from -j to +j by integer steps
| | Projection of the magnetic moment (μz) = ±9,284 10-24 J/T
| | Parity (P) = accordind to context
| | Position, momentum and total energy
D7.5. Quantum calculation methods :
All quantum calculation methods aim to calculate the possible values of observables and their measurement probabilities, but they do so in different ways depending on the application domains. These include :
Warning : It is common to omit certain universal constants from equations, including Planck's constant (h), reduced Planck constant (h'), light speed (c), Identity matrix (I) and gravitational constant (G).
Calculation methods include :
D7.5.1. Non-relativistic Schrödinger-type methods :
These approaches study the time evolution of the quantum state |Ψ> (i.e. wave function Ψ(x, t)), while the observables remain fixed unless the potential V(x, t) is explicitly time-dependent.
They are used particularly in quantum chemistry and follow the Schrödinger equation (1926, Nobel Prize in Physics 1933).
In particular, for a spinless particle of mass m, moving in one-dimensional space and subject to a potential V(x), this equation is written as :
(L1) i h' dΨ(x, t)/dt = -(1/2)(h'2/m)(d2Ψ(x, t)/dx2) + V(x) Ψ(x, t)
where h' is the reduced Planck constant (or Dirac constant = h' = h/(2 π))
and h is Planck's constant (h = 6.626 10-34 J.s).
See example of calculation using the continuous Schrödinger method and example of calculation using the discretized Schrödinger method.
D7.5.2. Relativistic Schrödinger-type methods :
The time evolution of the quantum state is described by wave equations generalizing the Schrödinger equation for particles moving at speeds close to that of light. We can cite :
1. Dirac equation for relativistic particles with spin 1/2 (examples : electron, neutrino).
In particular, for a free particle, this equation is written :
(D1) (i h' γμ dμ - m c I) Ψ = 0
where :
Ψ is the four-component Dirac wavefunction, called spinor, which simultaneously encodes the two spin eigenstates ("up"/"down"), the positive/negative energy solutions (particle/antiparticle), and their relativistic coupling, as follows :
- When momentum p is zero, the four components decompose into two distinct pairs. The first (Φ) encodes the probability amplitudes associated with the spin eigenstates of the particle (e.g., electron). The second (Χ) encodes those of the corresponding antiparticle (e.g., positron).
- As soon as p ≠ 0, the four components describe either a particle (positive energy) or an antiparticle (negative energy). Each individual solution remains a four-component state where spin (described by the Pauli matrices σ) and momentum (vector p) are coupled. One of the pairs encodes the spin eigenstates inherited from the rest frame, modulated by the motion. The other pair encodes their relativistic modification by connecting the two pairs via the total energy E.
m is the mass of the particle at rest.
I is the 4x4 Identity matrix
γμ are specific 4x4 matrices introduced by Dirac, with the index μ ranging from 0 to 3 (0 corresponding to time).These matrices are as follows in standard Pauli-Dirac representation :
γ0 =
(I 0)
(0 -I)
γi =
(0 σi)
(-σi 0)
γ5 = i γ0 γ1 γ2 γ3
(0 I)
(I 0)
in which σi are the 2x2 Pauli matrices and I is the 2x2 identity matrix.
The γμ matrices satisfy the Lorentz group anticommutation relation : {γμ, γν} = γμ γν + γν γμ = 2 gμν I avec gμν = Minkowski metric and I = 4x4 Identity matrix.
dμ are the partial derivatives with respect to the coordinates xμ = (ct, x1, x2, x3) in Minkowski spacetime.
γμ dμ implies a summation over the index μ according to the Einstein summation convention.
The Dirac equation therefore relates the dynamical properties of the particle (energy and momentum via the differential operator i h' γμ dμ) to its proper mass m.
See example of calculation using the Dirac method.
2. Klein-Gordon equation for relativistic particles with spin 0 (example : Higgs boson).
3. Proca equation for relativistic particles with spin 1 (examples : photon, W and Z bosons).
4. Rarita-Schwinger equation for relativistic particles with spin 3/2 (example : gravitino).
5. Generalizations of the Rarita-Schwinger equations for relativistic particles with half-integer spin greater than 3/2.
6. Linearized Einstein equations for the massless spin-2 graviton.
All these equations are invariant under the Lorentz-Poincaré transformation, which makes them compatible with restricted relativity.
However, the interpretation of these equations within the framework of a single-particle theory leads to certain inconsistencies. This is why Quantum Field Theory is essential as a more general and coherent framework.
D7.5.3. Heisenberg-type methods :
These approaches study the temporal evolution of observables, while the quantum state remains fixed.
They are used particularly in quantum operator calculations and quantum field theory. They follow the Heisenberg equation :
(H1) dA/dt = (i/h') [H, A] + DA/Dt
where :
A is the operator A(t) that represents the observable to be studie (e.g., position x(t) or momentum p(t))
H is the Hamiltonian operator of the system
[H, A] is the commutator between H and A, defined by : [H, A] = H A - A H
DA/Dt is the explicit derivative of the operator A in Schrödinger representation, obtained by differentiating only its time part. For example, if A(t) = cos(ω t) X, then DA/Dt = -ω sin(ω t) X
See example of calculation using the Heisenberg method.
D7.5.4. Dirac-type methods :
These approaches combine the time evolution of the quantum state and observables by describing the interactions between relativistic particles within the framework of quantum field theory, particularly in quantum electrodynamics through perturbative calculations and Feynman diagrams.
These approaches use an extended version of the relativistic Dirac equation for a free spin-1/2 particle.
D7.5.5. Advanced Algebraic Methods :
These general methods, based on algebraic tools (matrices, operators, Lie algebras), are used when it is difficult or even impossible to exactly solve the equations of motion, whether differential (Schrödinger-type), matrix (Heisenberg-type) or interactional (Dirac-type).
They allow the solution of simple systems (atoms, small molecules) or more complex systems (large molecules, materials) by providing exact or approximate solutions.
These include :
- Perturbation theory, which is used when the system can be considered a modification of a solvable case.
- Variational method, which provides an estimate of the energies of the bound states by minimizing a trial function.
- Ab initio approaches, which approximately solve the Schrödinger equation from first principles, without resorting to empirical parameters.
D7.5.6. Numerical methods :
These methods are used when it is impossible to obtain analytical solutions to equations.
These include the Monte Carlo method, the finite difference method, and the Lanczos method.
D7.6. Example of calculation using the continuous Schrödinger method :
The following example illustrates quantum computations using the Schrödinger equation.
Assumptions :
We consider a free, non-relativistic, massless, spinless particle located in a one-dimensional infinite potential well.
The time evolution of the wave function Ψ is then given by the Schrödinger equation (relation L1).
(L1) i h' dΨ(x, t)/dt = -(1/2)(h'2/m)(d2Ψ(x, t)/dx2) + V(x) Ψ(x, t)
When we are looking for the eigenstates Ψj of the system (numbered by the index j), the wave function Ψj(x,t) can be decomposed into a stationary spatial part and an oscillating temporal part, in the form :
(L2) Ψj(x,t) = Ψj(x) T(t)
The relation (L1) then becomes :
(L3) i h' (1/T) dT/dt = -(1/2)(h'2/m) (1/Ψj(x)) (d2Ψj(x)/dx2) + V(x)
Since the left-hand side depends only on t and the right-hand side only on x, they are equal to a constant Ej (total energy of the particule in the eigenstate Ψj).
Spatial equation :
Consequently, relation (L3) becomes :
(S1) -(1/2)(h'2/m) (d2Ψj(x)/dx2) + V(x) Ψj(x) = Ej Ψj(x)
If the infinite potential well is of width L, we also have :
(S2) V(x) = 0 for 0 < x < L and V(x) = ∞ for x ≤ 0 or x ≥ L
Inside the well, equation (S1) then becomes :
(S3) d2Ψj(x)/dx2 + kj2 Ψj(x) = 0
with : kj = (2 m Ej)1/2 / h'
The general solution is therefore :
(S4) Ψj(x) = A sin(kj x) + B cos(kj x)
where A and B are arbitrary constants.
For x = 0, Ψj(x) = 0, hence B = 0
For x = L, Ψj(x) = 0, hence A sin(kj L) = 0, which requires discrete values for kj and Ej such that :
(S5) kj = j π/L
(S6) Ej = (1/2)(h' kj)2 /m = (1/2)(j π h'/L)2 /m
with j being a non-zero positive integer (Ψj cannot be zero everywhere in the well).
Finally, we obtain :
(S7) Ψj(x) = A sin(j π x/L)
It remains to calculate A taking into account the normalization condition of Ψj(x, t) :
(S8) ∫0 to L [|Ψj(x)|2 dx] = 1
Given relation (S7) and the trigonometric identity : sin2(θ) = (1/2) (1 - cos(2 θ)), we then obtain :
1 = ∫0 to L [(1/2) A2 (1 - cos(2 j π x/L)) dx] = (1/2) A2 (∫0 to L [dx] - ∫0 to L [cos(2 j π x/L) dx])
The first integral is [x]0 to L = L
The second integral is (L/(2 j π)) [sin(2 j π x/L)]0 to L = 0
Hence : A = ±(2/L)1/2
We conventionally take the positive value of A because a wave function can always be multiplied by a global phase factor (such as -1 or even eiθ) without changing the physical predictions.
Relation (S7) then becomes :
(S9) Ψj(x) = (2/L)1/2 sin(j π x/L) with j a non-zero positive integer
Time equation :
Taking into account the constant Ej, relation (L3) becomes :
(T1) dT(t)/dt + i Qj T(t) = 0
with :
(T2) Qj = Ej/h' = (j π/L)2 h'/(2 m)
which has the following solution :
(T3) T(t) = Cj e-i Qj t
with Cj being an arbitrary complex constant equal to any phase factor of modulo 1 (Cj = ei θj with θj being a real number) in order to satisfy the normalization condition for Ψj(x, t) (Relation S8).
To simplify the calculations, we conventionally take Cj = 1. But this choice is arbitrary and must be revised if interferences or superpositions of states are studied, because the relative phases between different states play a crucial role in these situations.
Complete wave function :
Given relations (L2)(S9)(T3), the complete normalized wave function is therefore :
(C1) for 0 < x < L : Ψj(x,t) = Ψj(x) T(t) = (2/L)1/2 sin(j π x/L) ei θj e-i Qj t with j a non-zero positive integer ; otherwise : Ψj(x,t) = 0
For any value of j, there are always two nodes at the ends of the well (x = 0 and x = L) and (j - 1) additional nodes inside the well.
The ground state (j = 1) corresponds to : Ψ1(x,t) = (2/L)1/2 sin(π x/L) ei θ1 e-i Q1 t with two nodes at the ends of the well.
The first excited state (j = 2) corresponds to : Ψ2(x,t) = (2/L)1/2 sin(2 π x/L) ei θ2 e-i Q2 t with an additional node.
etc.
Probability amplitudes :
The probability density ρ is then written :
(D1) ρ = |Ψj(x,t)|2 = (2/L) sin2(j π x/L)
Note that this probability density is independent of time, which characterizes a stationary state.
Measurements of the observable :
Given relation (T2), the energy Ej of the particle in the eigenstate Ψj(x) is written :
(O1) Ej = (j π h'/L)2/(2 m) = (j h/L)2/(8 m) with j a non-zero positive integer
Conclusion :
- If the particle is in an eigenstate Ψj(x), its measured energy will always be Ej.
- If the particle is in a superposition of eigenstates Ψj(x) = ∑j [cj Ψj(x)], its measured energy will be Ej with a probability |cj|2 where cj is the superposition coefficient.
D7.7. Example of calculation using the discretized Schrödinger method :
The following example is the same as the previous one assuming that the wave function Ψ(x) is discretized on a set of N points {x1, ..., xi, ..., xN} inside the interval [0, L].
Discretized Schrödinger equation :
Let j be the index which numbers the different eigenstates Ψj of the quantum system.
Be careful not to confuse the indices i and j : The index j, although limited to N in this discretized representation, is not intrinsically linked to the index i of the spatial discretization points and could, in principle, extend to infinity in a continuous quantum system. This distinction is fundamental to avoid any confusion between the physical nature of quantum states (indexed by j) and their discrete digital representation (indexed by i).
The second-order Taylor expansion of Ψj(xi+1) and Ψj(xi-1) is written :
Ψj(xi+1) = Ψj(xi) + Δ dΨj(xi)/dx + (1/2) Δ2 d2Ψj(xi)/dx2
Ψj(xi-1) = Ψj(xi) - Δ dΨj(xi)/dx + (1/2) Δ2 d2Ψj(xi)/dx2
where Δ is the spacing between the discretized points.
By adding these two relations, we obtain the second derivative d2Ψj(x)/dx2 in discretized form as follows :
d2Ψj(xi)/dx2 = (Ψj(xi+1) - 2 Ψj(xi) + Ψj(xi-1)) / Δ2
In the example, this gives :
- spacing Δ = L/(N + 1)
- left limit : Ψj(x0) = Ψj(0) = 0
- right limit : Ψj(xN+1) = Ψj(L) = 0
The Schrödinger equation (relation S1) in its discretized form then becomes a matrix equation for any eigenstate Ψj :
f H Ψj = Ej Ψj
with :
f = multiplicative factor = -(h'/Δ)2/(2 m)
Ψj = column vector of components Ψj(xi)
Ej = eigenenergy associated with the eigenstate Ψj
H = hermitian matrix =
(-2 1 0 0 ... 0 0 0)
( 1 -2 1 0 ... 0 0 0)
( 0 1 -2 1 ... 0 0 0)
( 0 0 1 -2 ... 0 0 0)
( . . . . . . .)
( 0 0 0 0 ... -2 1 0)
( 0 0 0 0 ... 1 -2 1)
( 0 0 0 0 ... 0 1 -2)
It now remains to find the N eigenvalues λj of the matrix H and the N associated eigenvectors Ψj. Two methods exist :
Resolution by diagonalization of H :
This consists of finding, generally using numerical methods, two matrices D and P such that : H = P D P-1
in which :
- D is a diagonal matrix containing the eigenvalues of H on its diagonal
- P is a matrix whose columns are the eigenvectors associated with the eigenvalues
- P-1 is the inverse matrix of P
- Note that for a real symmetric matrix like H, then P is orthogonal (P-1 = PT).
Resolution by direct calculation :
The direct calculation of the N eigenvalues λj of the matrix H, generally using numerical methods, consists of solving the characteristic equation : det(H - λ I) = 0 where I is the identity matrix.
More quickly, since the matrix H is tridiagonally symmetric with a = -2 on the main diagonal and b = 1 on the two side diagonals, we obtain the solution : λj = a + 2 b cos(j π/(N + 1)). See demonstration below.
The eigenenergies Ej are then related to the eigenvalues λj by the relation : Ej = f λj
These energies represent the possible outcomes of a measurement of the system's energy.
The direct calculation of the N eigenvectors Ψj then consists of solving the system : (H - λ I) Ψj = 0, for example using the Gaussian method.
More quickly, since the matrix H is tridiagonally symmetric, the components i of the jth normalized eigenvector are given by : Ψji = (2/(N + 1))1/2 sin(j i π/(N + 1)). See demonstration below.
These eigenvectors describe the eigenstates of the particle, each eigenvector representing the spatial probability distribution of the particle for the corresponding energy. This means that |Ψji|2 = (2/(N + 1)) sin2(j i π/(N + 1)) gives the probability of finding the particle at position xi for the energy state Ej.
The normalization condition : ∑i |Ψji|2 = 1 for each eigenstate Ψj is then automatically verified.
Comparison with the continuous case solution :
Replacing i with x/Δ = x (N + 1)/L in the expression for Ψji, we obtain :
Ψj(x) = (2/(N + 1))1/2 sin(j π x/L)
which is equivalent to the spatial part of Ψj(x,t) in relation C1 to within a normalization factor ((2/(N + 1))1/2 instead of (2/L)1/2).
This difference reflects the different nature of the normalization involving a probability density in the continuous case, and point probabilities in the discrete case.
Concerning the energy Ej, it is written : Ej = f λj = f (-2 + 2 cos(j π/(N + 1)))
When N is large, given the limited expansion of the cosine around 0 : cos(α) = 1 - (1/2)α2 + o(α2), the expression Ej becomes : Ej = -f (j π/(N + 1))2
Given Δ = L/(N + 1), we also have : f = -(h'/Δ)2/(2 m) = -(h' (N + 1)/L)2/(2 m)
Replacing f in Ej, we then obtain : Ej = (j π h'/L)2/(2 m) which is equivalent to the energy Ej of the continuous case (relation O1).
These two equivalences show the consistency between the continuous and discrete approaches for this example of calculation.
Proof of : λj = a + 2 b cos(j π/(N + 1)) :
To simplify the notation, we set vi = Ψji
The equation (H - λ I) Ψj = 0 gives the following relation (R1) for each component i such that 2≤ i ≤ N - 1 :
(R1) b vi-1 + a vi + b vi+1 - λ vi = 0
We assume the solution is of the form vi = sin(i θj) where θj is a parameter to be determined.
Given the trigonometric identity : sin((i ± 1) θj) = sin(i θj) cos(θj) ± cos(i θj) sin(θj), relation (R1) then simplifies to :
(R2) λ = a + 2 b cos(θj)
The boundary conditions : v0 = vN + 1 = 0 then give :
v0 = 0 = sin(0 θj), which is satisfied.
vN + 1 = 0 = sin((N + 1) θj), which requires :
(R3) θj = j π/(N + 1)
Hence the complete solution : λj = a + 2 b cos(j π/(N + 1))
Proof of : Ψji = (2/(N + 1))1/2 sin(j i π/(N + 1))
Let Cj be a positive normalization factor such that : Ψji = Cj sin(i θj)
The norm of the vector Ψj must be equal to 1, which imposes :
1 = ∑i Ψji2 = Cj2 ∑i sin2(i θj)
It remains to calculate : ∑i sin2(i θj)
Given the trigonometric identity : sin2(α) = (1/2) (1 - cos(2 α)) and Euler's formula for the complex exponential : exp((-1)1/2 α) = cos(α) + (-1)1/2 sin(α), we obtain :
(R4) ∑i sin2(i θj) = (1/2) (N - S)
with : S = Real_part[∑i exp(2 i θj (-1)1/2)]
The sum of the exponentials forms a geometric series with common ratio r = exp(2 θj (-1)1/2) and first term r, which is written :
S = Real_part[r (1 - rN)/(1 - r)]
We also have :
r = exp(2 θj (-1)1/2) = exp(2 j π/(N + 1) (-1)1/2)
Let us assume that r = 1. This would imply that its argument is an integer multiple of 2 π, i.e. : 2 j π/(N + 1) = 2 k π with k integer, or after simplification : j = k (N + 1) which is impossible (since 0 < j < N + 1). The denominator (1 - r) is therefore never zero.
We also have :
rN = exp(2 θj (-1)1/2)N = exp((-1)1/2 2 j π N/(N + 1)) = exp((-1)1/2 2 j π (1 - 1/(N + 1)) = exp((-1)1/2 2 j π) / exp((-1)1/2 2 j π/(N + 1)) = 1/r
Hence finally : S = Real_part[-1] = -1
By transferring this value into relation (R4), we obtain :
∑i sin2(i θj) = (1/2) (N + 1)
Cj2 = 2/(N + 1)
Hence the normalized form of the vector Ψj :
Ψji = (2/(N + 1))1/2 sin(j i π/(N + 1))
D7.8. Example of calculation using the Heisenberg method :
The following example illustrates quantum computations using the Heisenberg equation.
Consider a one-dimensional quantum harmonic oscillator of mass m and angular frequency ω (relative to the spring stiffness).
The time evolution of any observable a(t) is then given by the Heisenberg equation (relation H1) in the form :
(H1) dA/dt = (i/h') [H, A] + DA/Dt
with :
A = operator A(t) which represents the observable a(t)
X = position operator
P = -i h' d/dx = momentum operator
(H2) H = P2/(2 m) + V(X) = Hamiltonian H of the system
V(X) = (1/2) m ω2 X2 = potential for a harmonic quantum oscillator
[H, A] = H A - A H = commutator between H and A
DA/Dt = explicit derivative of the operator A in Schrödinger representation
We are trying to calculate the two operators A(t) = X(t) and A(t) = P(t).
These are two basic operators whose mathematical definition does not explicitly depend on time, so : DA/Dt = 0
Calculation of [P, X] :
[P, X] Ψ = P (X Ψ) - X (P Ψ) = -i h' d(x Ψ)/dx - x (-i h' dΨ/dx) = -i h' (Ψ + x dΨ/dx) + i h' x dΨ/dx = -i h' Ψ
So [P, X] = -i h'
Calculation of [P2, X] :
Given the commutator property : [AB, C] = (AB)C - C(AB) = (ABC - ACB) + (ACB - CAB) = A[B, C] + [A, C]B, we can write :
(H3) [P2, X] = P[P, X] + [P, X] P = -2 i h' P
Calculation of [X2, P] :
(H4) [X2, P] = X [X, P] + [X, P] X = 2 i h' X
Calculation of [H, A] for A = X :
Given relation (H2), this can be written :
[H, X] = (1/(2 m)) [P2, X] + (1/2) m ω2 [X2, X]
Given relation (H3) and the property [X2, X] = 0, this can finally be written :
[H, X] = -i h' P/m
And the relation (H1) then becomes :
(H5) dX/dt = P/m
Calculation of [H, A] for A = P :
Given relation (H2), this is written :
[H, P] = (1/(2 m)) [P2, P] + (1/2) m ω2 [X2, P]
Given the property [P2, P] = 0 and relation (H4), this is finally written :
[H, P] = i h' m ω2 X
And relation (H1) then becomes :
(H6) dP/dt = -m ω2 X
Relations (H5)(H6) constitute a system of coupled differential equations whose solution is as follows :
X(t) = X(0) cos(ω t) + (1 /(m ω)) P(0) sin(ω t)
P(t) = P(0) cos(ω t) - m ω X(0) sin(ω t)
The operators X and P therefore oscillate harmonically at frequency ω depending on the initial conditions X(0) and P(0).
Note that we find the classical relation P(t) = m dX(t)/dt which is valid in the case of the example and in certain simple systems in Heisenberg representation, but which is not universal for all quantum problems. This relation is notably valid for any H of the form : P2/(2 m) + V(X) with V(X) combination of polynomial terms (V(X) = a + b X + c X2 + ...), given that [Xn, X] = 0 for any positive or zero integer n.
D7.9. Example of calculation using the Dirac method :
The following example illustrates quantum computations using the Dirac equation.
We consider a free Dirac fermion (without external interaction), described by a relativistic wave function.
The time evolution of the wave function Ψ is then given by the Dirac equation (relation D1) in the form :
(D1) (i h' γμ dμ - m c I4) Ψ(ct, x) = 0
which is explained as follows :
(D1*) i h' γ0 dΨ/d(ct) = (-i h' γk dk + m c I4)Ψ(ct, x)
with :
k = 1, 2, 3 (spatial components)
m = mass of the particle at rest.
I4 = 4x4 Identity matrix
γμ = specific 4x4 matrices introduced by Dirac.
x = 3D space vector = (x1, x2, x3)
dμ = partial derivatives with respect to the coordinates xμ = (ct, x1, x2, x3) in Minkowski spacetime.
In the case where we are looking for the eigenstatesΨj of the system (numbered by the index j), the wave function Ψj(ct, x) can be decomposed into a stationary spatial part and an oscillating temporal part, in the form :
(D2) Ψj(ct, x) = Ψj(x) T(ct)
The relation (D1*) then becomes :
(D3) i h' (1/T(ct)) dT(ct)/d(ct) γ0 Ψj(x) = (-i h' γk dk + m c I4) Ψj(x)
Multiplying both sides on the left by the matrix γ0, and taking into account the property (γ0)2 = I4, the relation D3 becomes :
(D4) i h' (1/T(ct)) dT(ct)/d(ct) I4 Ψj(x) = γ0 (-i h' γk dk + m c I4) Ψj(x)
For this relation to be true regardless of t and x, it is necessary that both sides be matrix operators acting identically on Ψj(x), therefore proportional to the Identity matrix (I4) with a common scalar factor Ej/c (the total relativistic energy of the particle in the eigenstate Ψj).
Spatial equation :
Consequently, relation (D4) becomes :
(DS1) γ0 (-i h' γk dk + m c I4) Ψj(x) = (Ej/c) I4 Ψj(x)
We then seek a solution in the form of a traveling plane wave :
(DS2) Ψj(x) = uj(pj) exp(i pj.x/h')
where :
pj = (p1, p2, p3) is the relativistic momentum vector in the inertial reference frame, expressed in 3D space = m γj vj where γj is the Lorentz factor (γj = (1 - vj2/c2)-1/2).
uj(pj) is a spinor associated with pj
pj.x is the 3D spatial scalar product = pjk xk
Given the spatial derivative dkexp(i pj.x/h') = (i pk/h') exp(i pj.x/h'), relation (DS1) simplifies to :
(DS3) γ0 (γk pk + m c I4) uj(pj) = (Ej/c) I4 uj(pj)
We then decompose the spinor uj(pj) into two Pauli spinors Φj and Χj such that :
(DS4) uj(pj) = (Φj, Χj)T
Given the expression for the matrices γ0 and γk, the DS3 relation then becomes a coupled system of two equations :
(DS5) σk pk Χj = (Ej/c - m c) Φj
σk pk Φj = (Ej/c + m c) Χj
Substituting Χj into the first equation, and taking into account the expression for the Pauli matrices σ, we obtain :
(Ej/c - m c)(Ej/c + m c) Φj = (σk pk)2 Φj = pj2 I2 Φj
Hence the expression of the observable Ej :
(DS6) Ej = ±(pj2 c2 + m2 c4)1/2
This so-called "dispersion" relationship corresponds to particles (electrons) with positive energy Ej and to antiparticles (positrons) with negative energy Ej.
It now remains to express Φj and Χj to find uj(pj)
For the electron (Ej > 0), the second equation DS5 gives :
(DS7) Χj = Φj σk pk/(Ej/c + m c)
If * denotes the complex conjugate without transposition and if wj is an arbitrary normalized Pauli spinor (such that (wj*)T.wj = 1), for example (1, 0)T for a spin oriented along the +z axis, then Φj can be chosen as follows :
Φj = ((Ej/c + m c)/(2 m c))1/2 wj to verify the normalization relation : (uj*(pj))T γ0 uj(pj) = 2 m c
For the positron (Ej < 0), the first equation DS5 gives :
(DS8) Φj = -Χj σk pk/(|Ej|/c + m c)
and Χj can be chosen as follows :
Χj = ((|Ej|/c + m c)/(2 m c))1/2 wj
Time equation :
Taking into account the constant (Ej/c) I4, relation (D4) becomes :
(DT0) i h' (1/T(ct)) dT(ct)/d(ct) I4 Ψj(x) = (Ej/c) I4 Ψj(x)
or :
(DT1) dT(ct)/d(ct) + i Qj T(ct) = 0
with :
(DT2) Qj = Ej/(c h')
which has the following solution :
(DT3) T(ct) = Cj exp(-i Qj ct) = Cj exp(-i Ej t/h')
with Cj being an arbitrary complex constant, which is equal to any phase factor of modulo 1 (Cj = ei θj with θj being a real number) in order to satisfy the normalization condition for Ψj(ct, x).
To simplify the calculations, we conventionally take Cj = 1. But this choice is arbitrary and must be reviewed if interferences or superpositions of states are studied, because the relative phases between different states play a crucial role in these situations.
Complete wave function :
Given the relationships (D2)(DS2)(DS4)(DS7)(DS8)(DT3), the complete normalized wave function for any eigenstate j is therefore :
(DC1) Ψj(t, x) = (Φj, Χj)T exp(i θj) exp(i pj.x/h') exp(-i Ej t/h')
This elementary solution Ψj(t, x) describes a free spin 1/2 fermion in the form of a relativistic plane wave, whose energy and momentum satisfy the relation Ej2 = pj2 c2 + m2 c4.
By superposition of these eigenstates (wave packets), it constitutes the basis of the relativistic quantum description, integrating the prediction of antimatter via negative-energy solutions.
Probability amplitudes :
Taking into account relation DS2, the probability density ρ is then written :
(DD1) ρ = (Ψj*(x))T Ψj(x) = (uj*(pj))T uj(pj)
D7.10. Similarities between quantum mechanics and classical mechanics :
Classical mechanics, which is deterministic and based on well-defined trajectories, contrasts with quantum mechanics which is based on probabilities, superpositions of states and other fundamental principles specific to its field.
However, despite these fundamental conceptual differences, the two approaches share several similarities :
- Description of the isolated system in terms of objects (examples : particles, solids) and internal or external interactions (examples : forces, fields, quantum interactions)
- Intrinsic data (or properties) (examples : mass, dimensions, spin, quantized energy levels of an atom)
- Observables (examples : position, velocity, energy, wave function, eigenvalue)
- Initial conditions (at t = 0) and boundary conditions of the system (example : boundary conditions for a vibrating string)
- Conservation of certain physical quantities (examples : momentum, angular momentum, energy)
- Universal physical constants (examples : gravity acceleration (g), light speed (c), Planck's constant (h))
- Resolution framework (examples : laws of dynamics, Schrödinger equation)
- Certain mathematical formalisms (examples : differential and integral calculus, linear algebra, differential equations)
- Calculation of observables (with deterministic or probabilistic results)
- Evolution of the system over time (examples : trajectories, wave function)
- Analysis and interpretation of results by comparing theoretical predictions and experimental observations, allowing models to be validated or adjusted.
D7.11. Sources relative to quantum physics :
[ASP] Alain Aspect, Si Einstein avait su, Odile Jacob, 2025.
[BOU] Alain Bouquet, Noyaux et particules.
[COH] Cohen-Tannoudji, Mécanique quantique, Tome I, CNRS Editions
[CHA] ChatGPT, le moteur d'Intelligence Artificielle développé par OpenAI.
[PER] Perplexity, le moteur d'Intelligence Artificielle développé par Perplexity AI.
Tying a knot requires precise, controlled movements adapted to the situation.
Neither a simple video nor the advice of a renowned author can, on its own, guarantee correct execution.
To learn and progress safely, it is therefore best to rely on official manuals, approved guides, or to follow a structured training course.
The rest of this page presents a compilation from several specialized works on knots, enriched to fill certain gaps and clarify the inaccuracies or ambiguities that can sometimes be encountered.
|
Key points to remember : In the case of heavy or variable loads (shocks), the techniques widely validated in climbing, caving, sailing and logging, are as follows : - Stopper knots : To block the end of a rope, the safest knot is the Figure-eight stopper knot. - Friction knots : To allow a rope to slide freely without a load, while ensuring automatic locking under load, the most commonly used self-locking knot in climbing is the Prusik hitch. - Bend knots : To join two ropes together, the knot prioritizing simplicity, strength, and ease of untie is the Zeppelin knot for ropes of the same or similar diameters, and the Double overhand bend for very different diameters. - Hitch knots : To attach a rope to a fixed point (bollard, tree, ring, etc.), the safest knot is the Double figure-eight knot on a bollard or tree, and the Anchor knot on a ring. - Lashing knots : To tie two rigid objects together (poles, logs, etc.) using a rope, the preferred knot for its strength is the Whipping assembly knot for two parallel objects and the Diagonal lashing for two objects crossing at any angle. |
Contents :
D8.1. List of knots :
The table below lists the main knots used in everyday life, classified by their main uses (cf. [PER][CHA]).
Legend of table : N/A = Not Applicable
| Main use | Knot | Tightening | Use | Heavy loads | Variable loads (shocks) | Ease of tying | Ease of untying (after heavy loading) | Risk of error (unstable knot) |
|---|---|---|---|---|---|---|---|---|
| Stopper knots | Figure-eight stopper knot (or Savoie knot) | locking | any kind of rope | yes | yes | simple | difficult | low |
| Overhand knot | locking | any kind of rope | no | no | simple | difficult | insufficient tightening | |
| Surgeon's knot | locking | suture thread | yes | yes | complex | very difficult | high | |
| Friction knots (or self-locking knots) | Prusik hitch | semi-sliding | different ropes | yes | yes | simple | difficult | low |
| Bend knots | Zeppelin bend (or Rosendahl bend) | locking | identical ropes | yes | yes | simple | easy | low |
| Double overhand bend | locking | any kind of ropes | yes | yes | simple | very difficult | insufficient tightening | |
| Fisherman's knot | locking | identical ropes | yes | yes | simple | difficult | high | |
| Reef knot | locking | identical ropes | no | no | simple | difficult | high | |
| Sheet join bend (or nautical weaver's knot) | locking | different ropes | no | no | simple | difficult | high | |
| Surgeon's join knot | locking | identical thin ropes | yes | yes | simple | difficult | high | |
| Hitch knots | Double figure-eight knot | locking | any Support | yes | yes | simple | difficult | low |
| Anchor knot | locking | Support = ring | yes | yes | complex | difficult | high | |
| Bowline knot | locking | any Support | in traction alone | no | complex | easy | high | |
| Alpine Butterly knot | locking | any Support in the middle of the rope | yes | yes | complex | easy | high | |
| Clove hitch | semi-sliding on a bollard, locking on a tree or ring | any Support | yes | no a bollard, yes on a tree or ring | simple | easy | high | |
| Round turn and two half hitches | locking | any Support | yes | yes | simple | difficult | low | |
| Constrictor knot | locking | any Support | yes | yes | simple | very difficult | high | |
| Surgeon's loop knot | locking | any Support | yes | yes | simple | difficult | insufficient tightening | |
| Paddle hook knot | locking | light fishing | no | no | simple | difficult | low | |
| Multi-turn slip knot (or multi-coil running knot) | sliding | any Support | yes | yes | simple | difficult | low | |
| Lasso knot (or Honda knot) | sliding | any Support | yes | yes | complex | difficult | high | |
| Barrel sling knot | sliding | vertical cylindrical Support | yes | no | complex | difficult | low | |
| Lashing knots (or rigid joining knots) | Whipping assembly knot | locking | two parallel logs | no | no | complex | difficult | high |
| Diagonal lashing | locking | two logs forming an angle | yes | no | complex | difficult | high | |
| Decorative knots | Windsor necktie knot | locking | tie | N/A | N/A | complex | easy | low |
| Chinese square knot | locking | scarf | N/A | N/A | complex | difficult | low | |
| French whipping | semi-sliding | rope | yes | yes | simple | difficult | high |
D8.1.1. Figure-eight stopper knot :

The figure-eight stopper knot (or Savoie knot) is a Locking Stopper knot at the rope end. It can support heavy or variable loads (shocks).
It is highly visible (bulky) and difficult to untie.
The figure-eight stopper knot is the safest standard for activities like climbing because it is simple to tie, offers a low risk of error, and has a symmetrical shape that allows for quick verification.
Note that this knot has an equally secure variant : the Double figure-eight knot. This latter knot, being bulkier, is rarely used in climbing as a Stopper knot.
The steps are as follows (see Figure above, cf. [MIS]) :
1. Pass the Running end over the Standing strand to form a small loop.
2. Make a complete loop around the Standing strand.
3. Pass the Running end through the loop from above (not from underneath).
4. Pull on both strands to tighten and form the figure-eight shape.
D8.1.2. Overhand knot :

The overhand knot is a Locking Stopper knot at the rope end, under light and constant loads (without shocks).
It is discreet (not bulky), simple to tie but difficult to untie (see Figure above).
Warning : This knot is unstable if it is not tight enough.
The double overhand knot is a variant of the overhand knot by passing the Running end twice through the loop, equivalent to a double-turned Capuchin knot (see Figure above).
It is simple to tie, stronger than the simple knot and less sensitive to imperfect tightening, but more difficult to untie.
Warning : This knot is unstable if it is not tight enough.
D8.1.3. Surgeon's knot :

The surgeon's knot is a Locking Stopper knot used to maintain tension between two sutures. It can support heavy or variable loads (shocks).
It is complex to tie and almost impossible to untie.
This knot is a variant of the Reef knot in which the first single turn of strand A around strand B is replaced by several successive turns, similar to the Capuchin knot (see Figure above, cf. [MAR1]). This modification increases friction and strengthens the knot.
Warning : This knot is unstable if incorrectly tied in steps 3, 5 and 6.
The steps are as follows, more complex than for the Reef Knot (see Figure above, cf. [MAR1][MAR2]) :
1. Identify a reference strand (A) and pass it over the other strand (B), the two strands forming a pair of horns.
2. Make two complete loops of strand A around B and reform the pair of horns.
3. Pass strand A over strand B again and make a second complete turn around B. Warning : If the crossing is made behind strand B instead of in front, the knot will be misaligned ("granny knot") and will come undone completely when you pull on the two long strands.
4. Check that the knot has two interlocking loops, with both strands of each loop passing either under or over the strand of the opposite loop.
5. Gently pull on both standing strands to "Capsize the knot" [MAR2]. Warning : Check the correct "Capsizing" as follows : 1. Front view : two diagonal, parallel strands pass through the center of the knot, 2. Back view : two loops appear at the ends of the knot.
6. Pull firmly on both pairs of strands to tighten the knot.
D8.1.4. Prusik hitch :

The Prusik knot is a Semi-sliding Friction knot made with a loop of cord wrapped around a main rope. It slides freely when unloaded and locks automatically under load in a symmetrical manner (in both directions of traction along the main rope), making it a simple and reliable system for climbing, rescue, or working at height.
It can support heavy or variable loads (shocks) but then becomes difficult to untie because of the tightly packed coils.
The Prusik knot is the most commonly used self-locking knot in climbing because it is simple to tie, offers a low risk of error, and has a symmetrical shape that allows for quick verification.
The steps are as follows (see Figure above, cf. [THE]) :
1. Use a cord closed into a loop (usually with a Double fisherman's knot) and position it on the main rope to form two sections : a short one and a long one.
2. Hold the short section and wrap the long section around the main rope, passing through the space between the main rope and the short section.
3. Continue wrapping, making several turns, always in the same direction and ensuring that each turn is tight around the main rope.
4. Pull gently on the long section to compress the turns against each other.
5. For added security, attach a carabiner to the long section forming the movable loop supporting the load, in order to connect it to your equipment or harness.
D8.1.5. Zeppelin bend :

The Zeppelin bend (or Rosendahl bend) is a Locking Bend knot. It allows you to join two ropes of the same diameter under heavy or variable loads (shocks).
It is simple to tie, offers a low risk of error, and has a symmetrical shape that allows for quick verification.
It has two distinct advantages that other Bend knots do not :
- It can be loaded before being fully tightened, which allows it to be used in situations where the load changes before final tightening.
- It is very easy to untie, even after supporting significant loads.
The Zeppelin knot, like the Double fisherman's knot, is the most secure Bend knot for ropes of the same diameter (but not for ropes of different diameters).
It is often preferred to the Double fisherman's knot for the two aforementioned advantages.
There are several methods for tying this knot. The steps of the so-called "symmetric" method are as follows (see Figure above, cf. [WIK, Zeppelin Knot]) :
1. Form two identical Bights, oriented in the same direction.
2. Overlap the two Bights head-to-tail (180°).
3. Take the Running end of the top Bight and cross it over its standing strand.
4. With this Running end, wrap it around both strands, passing underneath and emerging from the loop on the top.
5. Take the Running end of the other Bight and cross it under its standing strand.
6. With this Running end, wrap it around both strands, passing over and emerging from the loop on the bottom.
7. Tighten gradually and evenly by alternately pulling on the Running ends and then on the Standing strands.
8. Check that the knot has two parallel bars framed by two small ears, with Running ends perpendicular to Standing strands, the pattern being identical on the back side.
D8.1.6. Double overhand bend :

The double overhand bend is a Locking Bend knot used in climbing. It allows you to join two ropes of identical or different diameters under heavy or variable loads (shocks).
It is simple to tie and very difficult to untie.
Warning : This knot is unstable if it is not tight enough.
Thanks to its center being offset from the tension axis of the ropes, the two overhand knots compress each other at the butt without risk of twisting or slipping.
The double overhand bend is the most secure Bend knot on ropes of different diameters (and less so on ropes of the same diameter).
The steps are as follows (see Figure above, cf. [MAG1][MAG2][ARN2]) :
1. Align the two ropes parallel and in the same direction.
2. With the Running end pair, make a first Overhand knot encompassing both ropes.
3. Tighten it strand by strand by pulling successively and separately on each of the four strands. Check the symmetry of the center.
4. With the Standing end pair, make a second Overhand knot identical to the first and in the same direction. Bring this second knot against the first, then tighten it by simultaneously pulling on the two strands extending from the knot, on the side of the Standing strands.
5. Pull simultaneously and in opposite directions on the two Standing strands of each rope to compress the two knots against each other.
D8.1.7. Fisherman's knot :

The simple fisherman's knot (or English knot) is a Locking Bend knot. It allows you to join two ropes of the same diameter under heavy or variable loads (shocks). It is particularly suitable for thin ropes.
The simple fisherman's knot is actually the assembly of two Overhand knots tightly bound together, in perfect opposition.
It is simple to tie and difficult to untie.
Warning : This knot is unstable if it is incorrectly tied at steps 3 and 4.
The steps are as follows (see Figure above, cf. [PIN][MAR3]) :
1. Place the two strands A and B head-to-tail on your work surface, with their ends overlapping.
2. With strand A, tie a Overhand knot around strand B, but not too tightly, so that the two knots can slide towards each other when tightened.
3. Rotate the assembly 180° on your work surface (this is equivalent to reversing the top and bottom) and repeat the same actions with strand B. The 180° rotation ensures proper symmetry, as the two knots will fit together and not interfere with each other at the end of the assembly.
4. Gradually pull on the two long strands to bring the two knots together, fit them into the knot, and tighten them firmly against each other.
5. Check that the knot has two parallel bars on top and two crossed X on the bottom.

The double fisherman's knot is a variant of the simple fisherman's knot, even more secure but harder to untie.
The double fisherman's knot is actually the assembly of two Double-turn slip knots tightly bound together, in perfect opposition. Strand A wraps around strand B in the same way a Double-turn slip knot would wrap around its Standing strand.
Like the Zeppelin bend, the double fisherman's knot is the most secure Bend knot on ropes of the same diameter (but not on ropes of different diameters).
Warning :
- At the end of assembly, the two knots have the same general shape as two Double overhand knots placed side by side, but with one essential difference : End B does not pass through the loop left by A (see step 2 of the Figure "Simple fisherman's knot"), but it goes up inside the two turns (see step 4 of the Figure "Double fisherman's knot"), thus tightening the double twist more effectively.
- This knot is unstable if it is incorrectly tied at steps 6 and 7.
The steps are as follows (see Figure above, cf. [COR][MIN]) :
1. Place the two strands A and B head-to-tail on the work surface, with their ends overlapping.
2. With strand A, make a first turn around strand B, following the length of strand B towards its end and overlapping both strands.
3. Pass under B to begin the second turn, again returning towards the end of B. Both turns should be wide enough to allow a finger to pass through.
4. Complete the second turn, then pass end A through both turns.
5. Pull on the strands of the same knot, but not too tightly, so that the two knots can slide towards each other when tightened.
6. Rotate the assembly 180° on your work surface (this is equivalent to reversing the top and bottom) and repeat the same actions with strand B. The 180° rotation ensures proper symmetry, as the two knots will fit together and not interfere with each other at the end of the assembly.
7. Gradually pull on the two long strands to bring the two knots together, fit them into the knot, and tighten them firmly against each other.
8. Check that the knot has four parallel bars on top and two crossed X on the bottom.
D8.1.8. Reef knot :

The reef knot is a Locking Bend knot. It allows you to join two ropes of the same diameter under light and constant loads (without shocks).
It is simple to tie and difficult to untie.
Warning : This knot is unstable ("granny knot") if incorrectly tied in step 3.
The steps are as follows (see Figure above, cf. [GRU]) :
1. Identify a reference strand (A) and pass it over the other strand (B), the two strands forming a pair of horns.
2. Make a complete loop of strand A around B and reform the pair of horns.
3. Pass strand A over strand B again and make a second complete turn around B. Warning : If the crossing is made behind strand B instead of in front, the knot will be misaligned ("granny knot") and will come undone completely when you pull on the two long strands.
4. Check that the knot before tightening has two interlocking loops, with both strands of each loop passing either under or over the strand of the opposite loop.
5. Pull on both pairs of strands to tighten the knot.
D8.1.9. Sheet join bend :

The sheet join bend (or nautical weaver's knot) is a Locking Bend knot. It allows you to join two ropes of different diameters under light and constant loads (without shocks).
It is simple to tie and difficult to untie.
Warning : This knot is unstable if incorrectly tied in steps 1 and 2.
The steps are as follows (see Figure above, cf. [SCE][DIM]) :
1. Make a wide, open loop with the thicker strand. Warning : a too small loop can cause pinching when tightening, resulting in insufficiently gradual tightening and reduced, uneven friction.
2. Pass the thinner strand under the loop and loop it completely around both thicker strands of the loop in the same direction as the initial loop formation. Warning : Reversing the direction will result in an unstable knot.
3. Unlike the Reef knot, do not pass the thinner strand back through the loop, but rather along the side between the thicker and thinner strands. Warning : check that the two short ends emerge from the same lateral side of the knot.
4. Pull on the longer strands (thick and thin) to tighten the knot.
5. Variant to secure the knot when the load is heavy (double sheet bend) : Add a second turn, passing under the thinner strand.
D8.1.10. Surgeon's join knot :

The surgeon's join knot is a Locking Bend knot used in fishing. It allows you to join two thin ropes of the same diameter, under heavy or variable loads (shocks).
It is simple to tie and difficult to untie.
This knot is a variant of the Capuchin knot, made by doubling the rope (see diagram in Surgeon's knot).
Warning : This knot is unstable if it is not tight enough.
D8.1.11. Double figure-eight knot :

The double figure-eight knot is a Locking knot used as a Stopper knot or Hitch knot, particularly for tying up in the mountains. It can support heavy or variable loads (shocks).
It does not require an additional Stopper knot, is simple to tie and relatively error-free.
On the other hand, it is difficult to untie, especially after prolonged tension or repeated falls, which limits its use to permanent rather than temporary anchors.
This knot is a variant of the Figure-eight knot, made by doubling the rope (see Figure above, cf. [PET][ALP]).
This knot is the most secure Hitch knot on a bollard or tree type Support (but not on a ring).
In practice, however, the double figure-eight knot is not tied around a Support, as this would require pulling the entire length of rope through the loop. In fact, regardless of the Support (bolt, tree, or ring) :
A. First, form the loop at the end of the rope.
B. Make one or more Round turns around the Support with the Running end.
C. Close the knot with a connector (carabiner, quick link, etc.) linking the loop to the Standing strand, without re-tying. The anchoring is said to be "without tension" (if one or more Round turns) or "tensioned" (if only one quasi-turn of the tree).
D8.1.12. Anchor knot :

The anchor knot is a Locking Hitch knot, mainly usable on a ring or a shackle. It can support heavy or variable loads (shocks).
It is complex to tie and difficult to untie.
Its construction is similar to that of a Round turn and two half hitches, but the Half hitches are not identical : the first (a) is made on the two loops surrounding the ring, and the second (b) on the Standing strand (see Figure above, cf. [PON]).
This knot is the most secure Hitch knot on a ring (but not on a bollard or tree) because it offers optimal friction in a confined space thanks to the tight wrapping of the rope around the relatively small cross-section of the ring.
Warning : This knot is unstable if it is not tight enough.
D8.1.13. Bowline knot :

The bowline knot is a Locking Hitch knot that does not slip and can hold heavy loads under tension alone (without twisting forces, vibrations, or repeated shocks).
It is complex to tie and easy to untie, even after significant tension, making it ideal for temporary anchors.
Warning : The bowline knot can be unstable and dangerous (false bowline knot) if it is incorrectly tied in any of steps 3, 4, 5, or 6.
The steps are as follows (see Figure above, cf. [COM][ARN1]) :
Mnemonic : the snake comes out of the hole, goes around the tree, and goes back into the hole.
1. Make a large loop around the anchor point (tree, ring, etc.). The rope then has two strands :
- the Standing strand (called the "tree") which will bear the load,
- the Running end (called the "snake") which will be used to form the knot.
2. Form a loop with the tree (called the "hole").
3. Place the snake at the bottom of the hole, that is, in the center of the loop and on the same side as the tree relative to the plane of the loop. Warning : If the snake is placed on the opposite side, you will get a false bowline knot.
4. The snake exits the hole and goes around the back of the tree. Warning : If the snake crosses the tree before going behind it, you will get a false bowline knot.
5. The snake enters the hole parallel to the two strands of the anchor loop, without crossing them. Warning : If the snake crosses the two strands of the loop instead of remaining parallel, you will get a false bowline knot.
6. Then tighten the knot by holding the snake and the adjacent part of the anchor loop (part A) on one side, and the tree (part B) on the other, ensuring that they are moving in opposite directions relative to the hole. Warning : Otherwise, the hole can capsize like a sock and the knot will come undone completely.
7. To prevent any accidental loosening, add a Stopper knot (Figure-eight stopper knot for example) on the Running end, close to the bowline knot.

Note that this knot can be tied with one hand using a quick technique practiced in climbing.
Warning : The one-handed bowline knot can be unstable and dangerous (false bowline knot) if tied incorrectly, especially in step 6.
The steps are as follows (see Figure above, cf. [VOI][KIN][ARN1] :
1. Wrap the rope around your waist, then position the Running end over the Standing strand.
2. Rotate your wrist and make a Half hitch.
3. Turn your wrist over, palm facing up.
4. Pass the Running end under the Standing strand again, using the same hand.
5. Grasp the end and pull it over the Standing strand.
6. While holding the Standing strand with your left hand, pull the Running end of the rope through the loop where your wrist was, and reverse the knot by pulling on the Standing strand. Warning : Pull moderately, just enough to release the loop. Otherwise, the knot will be unstable or remain open.
7. Tighten the knot by pulling simultaneously on both strands (Running end and Standing strand).
8. To prevent any accidental loosening, add a Stopper knot (Figure-eight stopper knot for example) on the Running end, close to the bowline knot.
D8.1.14. Alpine Butterfly knot :

The Alpine Butterfly knot is a Locking Stopper knot, tied in the middle of the rope for intermediate anchors, tying in mid-rope, or isolating a damaged section of rope. It can support heavy or variable loads (shocks).
It is complex to tie and easy to untie, even under heavy tension.
Warning : This knot is unstable if it is incorrectly tied at any step.
There are several methods for tying this knot, including the "hand" method, which minimizes the risk of a false knot. The steps are as follows (see Figure above, cf. [WIK, Noeud de papillon alpin][SAU][NOD]) :
1. Place the rope vertically on the open palm of your hand and make three parallel turns, without overlapping the strands, working your way towards your fingers.
2. With your other hand, grasp the middle strand from underneath and pull it towards your fingers, forming a Bight.
3. Bring the Bight over the two remaining strands in your hand, wrap it around them, and bring it out again towards your fingers.
4. Remove your hand from the turns and tighten the knot firmly by pulling symmetrically on the Bight and the two strands extending from the rope.
5. Before loading, check that the knot has two small tabs on the front face and a well-formed X on the back face, which after loading transform into a flattened X on the front face and two parallel bars on the back face.
A variant of this knot exists (cf. [AND]), where the rope is placed behind the open palm of the hand (and not in front). The resulting knot is identical but with the left/right strands reversed.
D8.1.15. Clove hitch :

The clove hitch is a Semi-sliding Hitch knot on a bollard and a Locking Hitch knot on a tree or a ring. It allows you to secure a rope under tension to a fixed point, such as a hitch bollard.
It can support heavy constant loads (without shocks) on a bollard and variable (shocks) on a tree or a ring.
It is simple to tie and easy to untie.
Warning : This knot is unstable if incorrectly tied in steps 2 and 3.
On a bollard, the steps are as follows (see Figure above, cf. [ENA][ANI][NAU]) :
1. Make a Round turn around the bollard to absorb the rope tension and stabilize it [ENA]. This step is strongly recommended before tying the clove hitch itself (subsequent steps).
2. Form a first horizontal loop (Half hitch), passing the Running end under the Standing strand (ANI][NAU) and stacking it on the bollard.
3. Form a second horizontal loop in the same way as the first [ANI][NAU] and stack it on the bollard, creating the characteristic crossed shape of the clove hitch. Note that this second loop then appears reversed compared to the first. This is because the formation method (Running end under Standing strand), repeated twice, visually reverses the direction of the two loops.
4. Form a third loop and stack it on the bollard to secure the assembly in case the Standing strand becomes slack.

Note that this knot can be tied around a fixed point with no free end, such as a tree or a ring.
Warning : This knot is unstable if incorrectly tied in steps 2 and 3.
The steps are then as follows (see Figure above, cf. [LYO][QUE, timecode 18:30]) :
1. The Round turn around the tree is unnecessary in this situation because the first tight turn in the next step (step 1) is sufficient to absorb the rope tension and stabilize it.
2. Make a first complete loop around the tree (Half hitch), passing the Running end under the Standing strand. Tip : To keep this loop tight while making the second loop, it's best to temporarily wedge the Running end between the tree and the Standing strand, rather than simply placing it geometrically "under" the Standing strand [QUE, timecode 18:30].
3. Cross the Running end over the Standing strand and then make a second loop identical to the first.
4. Pull on the Running end to tighten the knot.
D8.1.16. Round turn and two half hitches :


The round turn and two half hitches is a Locking Hitch knot, usable on any external Support (bollard, tree, ring, etc.). It can support heavy or variable loads (shocks).
It is simple to tie, relatively error-free and difficult to untie.
Its tying is similar to that of a Clove hitch, with a preliminary Round turn, but the two Half hitches are made on the Standing strand and not on the bollard (see Figure on the left above, cf. [BUD, p.50]).
This difference means that the Half hitches work by wrapping and tightening on the Standing strand, and not by constricting around the bollard, which provides a better locking under load and also greater aptitude for variable loads (shocks).
For hitching on a bollard, the round turn and two half hitches is more secure than the Clove hitch because it is fully Locking and not Semi-sliding.
This knot has several variants, including :
- Variant with only one Half hitch (Half hitch after a round turn).
- Variant with first Half hitch replaced by a Complete hitch (see Figure on the right above, cf. [SAI]).
D8.1.17. Constrictor knot :

The constrictor knot is a Locking Hitch knot. It can support heavy or variable loads (shocks).
It is a variant of the Clove hitch around a tree, much tighter.
It is simple to tie and almost impossible to untie.
Warning : This knot is unstable if incorrectly tied in steps 1 and 2.
The steps are as follows (see Figure above, cf. [WIK, Noeud constricteur]) :
1. Make a complete turn around the tree, passing the Running end under the Standing strand.
2. Make a second turn, passing the Running end over the Standing strand and then under the first turn.
3. Pull on the Running end to tighten.
D8.1.18. Surgeon's loop knot :

The Surgeon's loop knot is a Locking Hitch knot used to pull a load. It can support heavy or variable loads (shocks).
This knot is a variant of the Capuchin knot, made by doubling the rope (see diagram in Surgeon's knot).
Warning : This knot is unstable if it is not tight enough.
D8.1.19. Paddle hook knot :


The paddle hook knot is a Locking Hitch knot, used in light fishing, which allows a fishing line to be attached along a paddle hook (without an eye), ensuring good alignment of the line with the paddle.
It is simple to tie, relatively error-free and difficult to untie.
It supports light and constant loads (without shocks).
Its construction is identical to that of the Whipping assembly knot on two parallel logs acting as a hook shank.
The steps are as follows (see Figures above, cf. [PEC]) :
1. Lay the line (or the rope) along the hook shank, making a loop on the side opposite the paddle, with a sufficiently long tail at the end.
2. Hold the loop firmly between your thumb and forefinger, then wrap the tail around the hook shank, from the loop towards the paddle, making about ten tight, close turns. In the case of a whipping assembly knot, traditional ropework often involves a reverse wrap (working towards the loop), which is still acceptable but offers less tensile strength [SCO].
3. Hold the last turn between your thumb and forefinger, then pass the free strand through the loop.
4. Pull simultaneously and fermly on both strands to tighten the knot.
5. In the case of a whipping assembly knot, for added strength, tie the two strands together with a Reef knot [SCO].
D8.1.20. Multi-turn slip knot :

A multi-turn slip knot is a Sliding Hitch knot that automatically tightens around an object when pulled. It can support heavy or variable loads (shocks).
It is simple to tie, relatively error-free and difficult to untie.
The steps are as follows (see Figure above, cf. [BUD, p. 62][KIM]) :
1. Make a loop with the Running end and then bring it back to the base of the loop by wrapping it around the Standing strand.
2. With the Running end, wrap the two strands of the base of the loop with several tight turns, working upwards towards the eye of the loop. The turns should be wide enough to allow a finger to pass through.
3. From the eye, pass the Running end under all the turns so that it comes out on the side of the Standing strand.
4. Pull on the loop and the Running end to tighten and compact the turns, keeping them tightly closed.
5. Pull on the Standing strand or apply a load, in order to tighten the loop around the object.
D8.1.21. Lasso knot :

A lasso knot (or Honda knot) is a Sliding Hitch knot that automatically tightens around an object when pulled. It can support heavy or variable loads (shocks).
It is complex to tie and difficult to untie.
Warning : This knot is unstable if it is not tight enough.
The steps are as follows (see Figure above, cf. [GET][WHY]) :
1. 60 cm from the end of the rope, tie a loose Overhand knot, leaving the loop loose.
2. At the end of the rope, tie a tight Overhand knot, which will serve as the Stopper knot.
3. Pass this Stopper knot through the loose loop by inserting it through the small oval opening located between the outgoing and incoming ends of the loop, then bring it out the other side. This automatically creates a small outer loop that will be the lasso's sliding loop.
4. Tighten firmly the loose loop against the Stopper knot to lock the assembly.
5. Pass the main rope through the small loop, leaving a large outer loop that will be the lasso loop.
6. Hold the lasso loop in your dominant hand, swing it above your head with a smooth, steady motion, aim at the target, and then throw the loop so that it wraps around the target. Then pull on the main rope to tighten the loop and lock the target.
D8.1.22. Barrel sling knot :

The barrel sling knot is a Sliding Hitch knot used to safely lift a cylindrical load in a vertical position (such as a barrel). It can support heavy or constant loads (without shocks).
It is complex to tie, relatively error-free and difficult to untie.
The steps are as follows (see Figure above, cf. [KNO]) :
1. Lay a large loop on the ground, forming a Figure-eight stopper knot.
2. Place the barrel on the main strand, in the center of the loop.
3. Raise the two Running ends vertically on either side of the barrel.
4. Tie the Running ends together with a secure Bend knot (usually a Double fisherman's knot) on the side of the barrel to prevent it from being crushed by the suspended load.
5. Test the tension before fully lifting.
D8.1.23. Whipping assembly knot :
The Whipping assembly knot is a Locking Lashing knot which allows to join two parallel poles together or to consolidate a fracture on a tool handle.
It supports light and constant loads (without shocks).
It is complex to tie and difficult to untie.
Warning : This knot is unstable if it is not tight enough.
Its construction is identical to that of the Paddle hook knot (see steps and associated Figure).
D8.1.24. Diagonal lashing :

Diagonal lashing is a Locking Lashing technique used to join two parallel logs that intersect at any angle (acute, right, or obtuse). It can support heavy constant tensions (without shocks).
It is complex to tie and difficult to untie.
Warning : This knot is unstable if the turns overlap or it is not tight enough.
The steps are as follows (see Figure above, cf. [MON][REG][QUE]) :
0. Create a flat surface on the logs at the joint to prevent them from rolling.
1. Tie a Clove hitch on one of the logs (starting point).
2. Wrap the two logs diagonally with three tight turns of rope, ensuring that the strands are parallel and do not overlap.
3. Repeat this process on the other diagonal. These two sets of turns form the characteristic cross of the diagonal lashing.
4. Wrap the contact area of the two logs with three turns of rope perpendicular to the diagonal turns.
5. Finish with a Clove hitch on one of the two logs to secure the lashing.
6. Add a Stopper knot (often a Figure-eight stopper knot) to the free strand of the final clove hitch to prevent accidental loosening.
D8.1.25. Windsor necktie knot :

The Windsor necktie knot is a Locking Decorative knot. It is an elegant and voluminous knot, shaped like a solid, symmetrical triangle without any frills. This knot requires a long tie made of thin fabric.
It is complex to tie, relatively error-free and easy to untie.
The steps are as follows (see Figure above, cf. [CRA]) :
Mnemonic : One turn around each loop and one turn around both loops.
1. Place the tie around your collar, with the wide strand to your left and the narrow strand slightly above your navel.
2. Cross the wide strand over the narrow strand.
3. Bring the wide strand up and pass it through the loop around your neck.
4. Bring the wide strand down to your right (first turn around your neck).
5. Bring the wide strand behind the knot, to your left.
6. Bring the wide strand up again and pass it through the loop around your neck.
7. Bring the wide strand down to your left (second turn around your neck).
8. Bring the wide strand forward over the knot, to your right (turn around the two previous turns).
9. Bring the wide strand up for the third time and pass it through the loop along your neck.
10. Insert the wide strand into the front loop formed at the front of the knot.
11. Tighten the knot by gently pulling on the wide strand, then adjust it to give it a symmetrical, triangular shape.
D8.1.26. Chinese square knot :

The Chinese square knot is a Locking Decorative knot that can be attractively tied on a scarf.
It is complex to tie, relatively error-free and difficult to untie.
The steps are as follows (see Figure above, cf. [SCC][CRE][DAR]) :
1. Cross one of the two strands of the scarf (called "active strand") over the other strand (called "inactive strand").
2. With the active strand, form an S with two inverted loops and three parallel segments, the bottom segment passing over the inactive strand and the other two under.
3. Pass the inactive strand under the three segments of the S, then over the S, and insert it into the top loop of the S.
4. Adjust the knot by pulling successively on the four ends of the strands.

Note that this knot can be tied on oneself using another technique practiced in scouting.
The steps are as follows (see Figure above, cf. [DAR]) :
1. Cross one of the two strands of the scarf (called the "active" strand) over the other strand (called the "inactive" strand) at a 90° angle, and wrap it around.
2. Place your finger under the knot behind the inactive strand and wrap it back, forming a loop around your finger.
3. Continue wrapping the inactive strand around and bring it to the front.
4. Pass the active strand through the loop in place of your finger.
5. Adjust the knot by gently pulling on the four ends of the strands.
D8.1.27. French whipping :

The French whipping is a Semi-sliding Decorative knot, also used as a handle or as a weight on a rope. It can support heavy or variable loads (shocks).
It is simple to tie and difficult to untie.
Warning : This knot is unstable if it is incorrectly "Capsized" or insufficiently tightened.
The steps are as follows (see Figure above, cf. [SCA]) :
1. Make an Overhand knot, passing the Running end through the loop several times.
2. Pull on both opposite ends to "Capsize the knot.
3. Continue pulling until the knot is completely tight.
4. Check that the knot appears as a cylinder of tightly packed turns.
Note that a double-turned capuchin knot is equivalent to the Double simple knot.
D8.2. Glossary :
Bight = Loop of a rope in the shape of an elongated U, without crossing the strands.
Capsizing of a knot = Step that occurs after several turns of one strand around another, as in the case of the French whipping and the Surgeon's knot. By simultaneously pulling on the Standing strands, the turns reorganize around the central part of the knot, which compacts the whole, changes the geometry of the knot, and increases its internal friction.
Complete hitch = Complete Overhand knot around an Support, almost always an outgoing Standing strand and sometimes an external Support such as a tree. The Running end wraps around this Support, goes around the Standing strand (separate from the Support), which secures the hitch by increasing friction, then enters the loop formed between the Support and the Standing strand (see Round turn and two half hitches).
Round turn = Complete turn of a rope around a Support before the Running end crosses the starting point (Standing strand), which, in practice, often makes one and a half turns around the circumference of the Support (see Clove hitch).
Half hitch = Overhand knot around an Support, but without going around the Standing strand. The Running end wraps around this Support, without going around the Standing strand, then enters the loop formed between the Support and the Standing strand (see Clove hitch on a tree). The half hitch is actually an incomplete Overhand knot, whose loop is held only by the Support.
Half hitch after a round turn = Temporary Bend knot consisting of a Round turn around a Support followed by a Half hitch around the Support.
Main use =
- Stopper knots = Used to block the end of a rope and prevent fraying or slipping.
- Friction knots (or self-locking knots) = Used to allow a rope to slide freely without a load, while ensuring automatic locking under load.
- Bend knots = Used to join two ropes together.
- Hitch knots = Used to attach a rope to a fixed point (bollard, tree, ring, etc.).
- Lashing knots (or rigid joining knots) = Used to tie two rigid objects together (poles, logs, etc.) using a rope.
- Decorative knots = Used to create aesthetic patterns.
Munter (or Italian) hitch = Friction knot on a carabiner.
Running end = Free end of the rope that is manipulated to form the knot.
Standing strand = Fixed part of the rope that remains still during the knot-tying process and bears the load.
Support = External anchor point (bollard, tree, ring, etc.) or internal such as a part of rope (outgoing Standing strand), serving as a fixed base for winding the Running end during a Half hitch or a Complete hitch.
Tying = The ease of tying a knot is defined as its ability to be made quickly and correctly in a situation, because it relies on an elementary spatial choreography of gestures and strands.
Tightening =
- Locking knot : Locks onto the Standing strand with or without load, and slides back after being unloaded only with manual intervention (example : Figure-eight stopper knot).
- Sliding knot : Slides along the Standing strand without load, locks under load, and slides back after being unloaded only with manual intervention (example : Multi-turn slip knot).
- Semi-sliding knot : Slides along the Standing strand without load, locks under load, and slides back spontaneously (without manual intervention) after being unloaded (example : Prusik hitch).
Unstable knot = Poorly executed knot, therefore unreliable and able to untie itself spontaneously under load (without manual intervention).
Untying = The ease of untying a knot is defined as its ability to be undone after supporting a heavy load.
D8.3. Sources :
[ALP] AlpineSavvy, Using a rope to make a tensionless tree anchor.
[AND] andreba, Noeud papillon alpin (Youtube, 01:45).
[ANI] Animated knots, Clove Hitch - Loops.
[ARN1] ArnO'Voyages, [Tuto'Escalade] Le noeud d'encordement en CHAISE - Comment faire - Quelle utilisation ? (Youtube, 04:08).
[ARN2] ArnO'Voyages, [Tuto'Escalade] Le noeud de jonction - Noeud simple - descente en rappel - Comment faire ? (Youtube 02:52).
[BUD] Budworth Geoffrey, Guide des noeuds, Parragon Books Ltd, 2006.
[CHA] ChatGPT, le moteur d'Intelligence Artificielle développé par OpenAI.
[COM] comment_economiser.fr, Le Noeud de Chaise est le Noeud le Plus Utile : Solide, Facile à Faire et à Défaire..
[COR] Cordévasion, Comment faire un noeud de pêcheur double en escalade.
[CRA] E.L. Cravatte, Le noeud Windsor.
[CRE] Les Créatifs, Nouage : une boucle chinoise.
[DAR] Dargis Pierre, Noeud carré (Youtube, 02:05).
[DIM] Dimitri Elledge, Comment faire le noeud d'écoute (+noeud d'écoute double) - Noeud de jonction! (Youtube, 04:45).
[ENA] Enautic, Le Noeud : 1 tour mort et 2 demi clés (Youtube, 00:54).
[FRA] La fraternité du scoutisme, Assemblage du bois.
[GET] gettin, A Cool Guide demonstrating how to Tie a Lasso.
[GRU] Grupo Scout Barrio La Victoria, Nudo rizo.
[KIM] kimoc13, Faire le noeud coulant facilement. (Youtube, 04:30).
[KIN] KINRED, Faire le noeud de chaise avec une main les yeux fermés ! (Youtube, 00:23).
[KNO] knots.neocities.org, Figure 8 Barrel sling.
[LYO] http://lyon.noeuds.free.fr, Les noeuds - Le noeud de cabestan.
[MAG1] Montagnes Magazine, Bien choisir son noeud pour rabouter 2 cordes.
[MAG2] Montagnes Magazine, Comment faire un noeud de jonction de corde ?.
[MAR1] Marsala, Noeud de chirurgien (Youtube, 01:39).
[MAR2] Marsala, Matelotage : Noeud de chirurgien (Youtube, 01:18).
[MAR3] Marsala, Noeud de pecheur simple.MOV (Youtube, 02:08).
[MIN] Minute Forme, Réaliser un noeud double pêcheur (Youtube, 01:57).
[MIS] La Misaine, Noeuds marins.
[MON] Orientacion en el campo y tecnicas de Montanismo - Nudos, amarres y estructuras.
[NAU] Nautisme-pratique.com, le noeud cabestan.
[NOD] Nodo Farfalla (Alpine Butterfly Knot): Tutorial(Youtube, 00:33).
[PEC] Pêche pro, Les noeuds.
[PER] Perplexity, le moteur d'Intelligence Artificielle développé par Perplexity AI.
[PET] Petzl, Noeuds.
[PIN] Pinterest, Noeud marin.
[PON] Pontonniers de Genève, Cordages.
[QUE] Le Quercus, Les Noeuds de brêlages (Youtube, 25:08).
[REG] Regroupement scout francophone 64e Clarence-Rockland, Brêlage en croix.
[SAI] True Sailor, Noeud tour-mort deux demi-clés.
[SAU] Sauvetage Rivière Boréal, 8 noeuds utiles pour le sauvetage en eau vive et en eaux vives.
[SCA] Science Maison, Noeud de capucin.
[SCC] Science Maison, Noeud carré décoratif.
[SCE] Science Maison, Noeud d'écoute (oeud de tisserand).
[SCO] ScoutWiki, Surliure.
[THE] The Knots Manual, How to Tie a Prusik Knot.
[VOI] Voile & Moteur, Matelotage : Variations sur noeud de chaise.
[WHY] WhyKnot, Apprenez à nouer un lasso de cow-boy (Youtube, 01:49).
[WIK] Wikipedia, Noeud constricteur.
[WIK] Wikipedia, Noeud de papillon alpin.
[WIK] Wikipedia, Noeud de Zeppelin.
See detail.

E4.1. Introduction :
Genetics is the science that studies the organization, functioning, regulation and modification of genes, both in their transmission from one generation to another and in their expression within the same individual.
It includes six major scientific fields [PER][CHA] :
1. Genome organization and cell manufacturing
Each cell in the human body contains a complete copy of the organism's genetic material (the genome), carried by DNA (Deoxyribonucleic Acid).
This genome contains all the instructions necessary to produce all of the body's proteins. However, in practice, each cell expresses only a portion of the genes, depending on its specialization. For example, a muscle cell will produce mainly contractile proteins, and few or no proteins specific to neurons or immune cells.
Proteins play an essential role in the body. On the one hand, they perform structural functions by maintaining and repairing tissues. On the other hand, they act as regulators of vital functions, notably participating in genetic regulation (histones and transcription factors), hormonal regulation (hormones), digestive regulation (enzymes), oxygen transport in the blood (hemoglobin), and immune defense (antibodies).
Each cell thus produces two main types of proteins :
- Effector (or target) proteins, such as structural proteins, transport proteins, hormones, enzymes, that perform the body's cellular and physiological functions.
- Regulatory proteins, such as histones and transcription factors, that control gene expression.
Once produced, proteins are transported to their sites of action (cells, organs, tissues). Some, like hormones, travel through the blood to reach distant organs.
2. Genetic Regulation
Genetic regulation is the control of gene expression, particularly through modulation of DNA accessibility, without modifying the DNA sequence.
The main players in this mechanism are :
- Non-coding DNA sequences (not translated into proteins), which consist mainly of Non-coding genes and Intergenic sequences.
- Regulatory proteins, which are of two main types : Histones ensuring the compaction of the DNA around them and therefore the modulation of its accessibility, and Transcription factors which bind to non-coding DNA sequences to activate or repress gene expression.
- Epigenetic modifications, which are reversible additions of chemical groups to DNA molecules and also to histone tails, altering DNA accessibility and therefore the body's response to internal and external stimuli.
- Long non-coding RNAs, which act as indirect regulators, for example, guiding proteins to specific regions of DNA.
3. Genetic Variation
Genetic variation is the production of genetic differences. The main mechanisms are as follows :
- Mutation : Lasting modification of the DNA sequence at the gene, chromosome, or entire genome level.
- Recombination (crossing-over) : Exchange of DNA segments between homologous chromosomes during meiosis, creating new genetic combinations.
- Polymorphism : Coexistence of several normal genetic forms in a population, as demonstrated by the ABO blood group system in humans, which produces a diversity of groups (A, B, AB, O, etc.).
- Transposition : Change in the position of a DNA segment within the genome.
- Genetic drift : Random change in the frequencies of different forms of a gene in a small population, often due to chance events (catastrophes, isolation) that reduce the number of individuals.
- Migration (or gene flow) : movement of individuals from one population to another, resulting in the arrival or departure of certain gene forms in the host population.
- Random mating : reproduction where partners are chosen at random, promoting genetic mixing within the population.
4. Genetic Repair
Genetic repair is the correction of errors or damage in DNA. The main mechanisms, classified by increasing severity of the damage, are as follows :
- Direct repair : For a slightly damaged base
- Base excision repair (BER) : For an absent or severely damaged base
- Copy error repair (MMR) : For an erroneous sequence following DNA replication
- Nucleotide excision repair (NER) : For a damaged sequence
- Single-strand break repair (SSB repair) : For a broken strand, with the intact second strand serving as a template
- Double-strand break repair (DSB repair) : For a broken double strand
5. Genetic Transmission
Genetic transmission is the transmission of hereditary information at the individual level (between cells of the same organism) or transgenerationally (from one generation to the next). The main mechanisms are as follows :
- Replication : Faithful copying of DNA before each cell division.
- Mitosis : Cell division of somatic (body) cells producing two identical daughter cells with the same number of chromosomes as the parent cell.
- Meiosis : Cell division of germ (reproductive) cells producing two gametes (egg and sperm), each containing half the number of chromosomes. This division does not fragment the genetic information but intelligently redistributes it between the gametes through shuffling and control mechanisms, allowing fertilization to reconstitute a complete and unique genetic heritage.
- Fertilization : Fusion of two gametes (egg and sperm) to form an egg cell (zygote) with a full chromosome number.
- Mendelian inheritance : Transmission of hereditary traits via genes located on nuclear chromosomes (therefore inherited from both parents), according to Mendel's laws.
- Non-Mendelian inheritance : Transmission of hereditary traits that do not follow Mendel's laws, either due to the location of genes outside the nuclear chromosomes (such as mitochondrial DNA inherited only from the mother, or chloroplast DNA), or due to specific mechanisms affecting nuclear genes (such as parental imprinting, incomplete dominance, dynamic mutation, sex-linkage).
- Epigenetic transmission : Transmission, at the individual or transgenerational level, of regulatory marks of gene expression, without modification of the DNA sequence.
6. Natural Selection
Natural selection is an evolutionary mechanism that sorts individuals according to their ability to survive and reproduce.
Given the hereditary variations between individuals, natural selection favors certain traits within this diversity : individuals carrying genetic characteristics that are advantageous for their survival and reproduction in a given environment produce more offspring.
This concept of natural selection evolved historically in four stages (illustrated by the giraffe) :
- Lamarck (inheritance of acquired traits, 1809) : The giraffe lengthens its neck to reach high leaves and passes this acquired trait on to its offspring.
- Darwin (natural selection, 1859) : In giraffes, those born with longer necks through random individual variation survive better and reproduce more, thus producing more offspring.
- Neo-Darwinism (modern genetics, Collective, 1930-1940) : In giraffes, those born with longer necks due to random genetic mutations (not environmentally driven) survive better and reproduce more, thus producing more offspring.
- Epigenetics (regulation of gene expression, Waddington, 1942) : In giraffes, in addition to random genetic mutations, difficulty reaching high leaves could alter the expression of genes involved in neck growth, without changing the DNA sequence. These epigenetic modifications could be temporarily passed on to their offspring.
In summary :
Cellular functioning, through its major functions (organization, production, regulation, variation, repair, transmission), subtly illustrates the dynamic balance between assimilation and accommodation, as described by Jean Piaget.
Like the intelligence of living organisms which constantly adjusts its patterns to integrate or transform experience, the cell assimilates most events according to its genetic and epigenetic programs. But it also knows how to accommodate, that is, adjust or remodel its mechanisms, in the face of novelty or disruption.
This adaptive balance, the driving force of cellular plasticity, provides, on a larger scale, the innovations that are influenced by natural selection.
E4.2. Cell description :
A hierarchical description of the eukaryotic cell (with nucleus) is given as follows [PER][CHA] :
Note : The number shown is relative to the adult human being.
Eukaryotic cell = Plasma membrane + Cytoplasm + Nucleus. Number = 37 trillion
|
| Plasma membrane = Envelope separating the interior and exterior of the cell.
|
| Cytoplasm = Cytosol + Organelles
| |
| | Cytosol = Aqueous medium containing ions, nutrients, and enzymes.
| |
| | Organelles = Free ribosomes + Endoplasmic reticulum + Mitochondria + Golgi apparatus + Lysosomes + Cytoskeleton
| | | Free ribosomes = synthesize proteins from messenger RNA. Number = 10 million
| | | Endoplasmic reticulum (ER) = Synthesizes lipids (smooth ER) and other proteins (rough ER, with attached Ribosomes).
| | | Mitochondria = Produce cellular energy (ATP) through cellular respiration. Contain their own DNA (mitochondrial genome). Number = 100 to 10,000 (according to cell type).
| | | Golgi apparatus = Sorts, packages and transports molecules (mainly proteins and lipids) to their final destination (internal or external to the cell).
| | | Lysosomes = Digest cellular waste. Number = 300 to 500
| | | Cytoskeleton = Maintains cell shape and participates in cell movement.
|
| Nucleus = Nuclear membrane + Nucleoplate + Chromatin + Nucleoli
| |
| | Nuclear membrane = Double envelope separating the interior and exterior of the nucleus.
| |
| | Nucleoplate = Gelatinous medium containing enzymes and ions.
| |
| | Chromatin = Nuclear genome + Regulatory proteins + Associated RNAs + Epigenetic modifications
| | |
| | | Nuclear genome = Set of Chromosomes. Number = 23 pairs of chromosomes.
| | | | Chromosome = Compacted DNA molecule (double helix consisting of two antiparallel strands of nucleotides) = Coding genes + Non-coding genes + Intergenic sequences
| | | | | Coding gene = DNA sequence containing the information necessary for protein synthesis. Number = 20,000 coding genes per nuclear genome.
| | | | | Non-coding gene = DNA sequence containing the information necessary primarily for functional RNA synthesis.
| | | | | Intergenic sequences = Non-coding DNA sequences located between two adjacent genes (coding or non-coding). They notably constitute the anchoring platforms for Regulatory proteins and also include a diversity of repeated sequences. Proportion = 90 % of the nuclear genome.
| | | | | Nucleotide = Phosphate group + Deoxyribose sugar + Nitrogenous base. Number = several million per chromosome
| | | | | | Nitrogenous base = Adenine (A), Thymine (T), Cytosine (C), or Guanine (G). Number = 3 billion pairs of nitrogenous bases per nuclear genome.
| | |
| | | Regulatory proteins = Histones + Transcription factors
| | | | Histones = Proteins that compact DNA around themselves and thus modulate its accessibility.
| | | | Transcription factors = Proteins that bind to non-coding DNA sequences to activate or repress gene expression.
| | |
| | | Associated RNAs = Main mediators of gene expression
| | | | Messenger RNA (mRNA) = Copies a coding Gene (the blueprint for protein production) and transports it to the Ribosomes.
| | | | Transfer RNA (tRNA) = Transports amino acids to the Ribosomes and positions them according to the provided blueprint.
| | | | Ribosomal RNA (rRNA) = Forms the backbone of the Ribosomes and assembles amino acids into protein chains according to the provided blueprint.
| | | | microRNA = blocks specific messenger RNA, preventing their translation and thus reducing the production of effector proteins.
| | | | Long non-coding RNA (IncRNA) = Indirect regulator, for example, guiding proteins to specific regions of DNA.
| | |
| | | Epigenetic modifications = Reversible additions of chemical groups to DNA molecules and histones, thus altering DNA accessibility.
| |
| | Nucleoli = Synthesize ribosomal RNAs. Number = 1 to 5
E4.3. Epigenetics :
Epigenetics constitutes a biological underpinning common to all acquisition-based learning (memory stabilization, brain plasticity, metabolic adaptations). It allows cells to encode lived experience through changes in gene expression without altering the DNA sequence, unlike genetic mutations.
This fundamental mechanism dynamically regulates gene expression according to the physiological or environmental context, thus allowing the organism to adapt effectively to internal and external stimuli, including :
- Climate variations (temperature, humidity)
- Dietary changes (deficiency, excess, nutritional quality)
- Habitat changes (urbanization, pollution, migration)
- Physiological stress (illness, intense exercise)
- Traumatic stress (emotional shock, violence)
This regulation is achieved through reversible chemical modifications, such as :
- DNA methylation, by adding methyl groups to the DNA.
- Modification of regulatory proteins (mainly histones) around which DNA is wrapped.
These modifications dynamically control access to genes and their expression levels, allowing their activation or repression without altering the underlying genetic content.
Two levels of plasticity are distinguished :
Individual plasticity : When stimuli are moderate or transient, the changes remain confined to somatic (body) cells and are not transmitted to subsequent generations.
For example :
- The Arctic fox changes its coat (white in winter and brown in summer). Fox cubs are born with a coat adapted to their season of birth, but their ability to change color then depends on environmental stimuli (study by Zimova M., Mills L.S., Nowak J.J., 2016).
- In humans, skin tanning in response to the sun is a temporary adaptation specific to each individual (study by Slominski A., 2004).
Transgenerational plasticity : When stimuli are intense or prolonged, the changes also affect germ cells (sperm and oocytes). These marks are then transmitted to offspring and influence their phenotypes (behavioral, physiological, and morphological traits) for one to three generations before fading.
For example :
- In water fleas (Daphnia), parental exposure to predator signals induces the development of morphological defenses (helmets or spikes) in the offspring, even if the young have never encountered a predator themselves (study by Tollrian R., 1995).
- Male mice exposed to prolonged cold give birth to offspring better adapted to low temperatures (study by Chan J.C., 2020).
- Male mice conditioned to fear an odor transmit a specific hypersensitivity to that odor to their offspring (study by Dias & Ressler, 2013).
- In humans, malnutrition before pregnancy in the mother or father can have a lasting effect on the child's health, even if the child subsequently grows up in a normal food environment (study by Gete DG., Waller M., Mishra GD., 2020).
In the case of cognitive learning, epigenetics is closely linked to brain plasticity (neural networks) at two complementary coding levels [MER] :
- A structural level : Learning modifies the strength and organization of synaptic connections between neurons, ensuring the storage and consolidation of acquired information (memory).
- A biological level : Learning induces epigenetic modifications in the genome of neuronal cells, which regulate the expression of genes involved in synaptic plasticity and stabilization of neuronal networks.
Warning : Despite the profound impact of intensive cognitive activity (such as musical practice) on brain plasticity and neuronal epigenetics, these changes remain strictly individual. To date, no hereditary mechanism, genetic or epigenetic, has been demonstrated to transmit these adaptations to offspring.
E4.4. RNA :
RNA (RiboNucleic Acid) is the dynamic relay between DNA and all cellular activities, ensuring the transmission, translation and regulation of genetic information within the cell.
All RNAs are synthesized by direct copying of DNA sequences (transcription) through the action of RNA polymerase, a special protein initially present in the cell and then produced by messenger RNA, like all other proteins.
Warning : No RNA is a protein. RNA polymerase, despite its name, is not an RNA but a protein (enzyme) that makes RNA.
A specific type of RNA, messenger RNA (mRNA), is a partial and targeted copy of genetic information, then transmitted to ribosomes (in the cell cytoplasm). Ribosomes then "read" this messenger RNA (coding RNA) as a blueprint for making (synthesizing) proteins.
Other types of RNA, known as non-coding RNA, do not contribute to protein production. They are functional and perform key regulatory functions, such as :
- Blocking specific messenger RNAs to prevent their translation (e.g., microRNAs), thereby reducing the production of effector proteins.
- Controlling access to DNA via epigenetic modifications (e.g., long non-coding RNAs), thereby modulating gene expression without altering the DNA sequence.
E4.5. Sources relative to genetics :
[CHA] ChatGPT, le moteur d'Intelligence Artificielle développé par OpenAI.
[MER] Karine Merienne, Anne-Laurence Boutillier, Régulations épigénétiques et plasticité cérébrale : vers de nouvelles thérapies dans les maladies neurodégénératives ?, 2016.
[PER] Perplexity, le moteur d'Intelligence Artificielle développé par Perplexity AI.
See detail.
 Last page update : December 27, 2025.
Last page update : December 27, 2025.