
| In English | Accueil/Contact | Billard | Bélier | SNH | Relativité | Botanique | Musique | Ornitho | Météo | Aide |

Cette page est destinée aux amoureux de la nature, du temps et des voyages.
Elle montre comment l'observation des Nuages et des Vents permet de prédire le temps sur 24 heures.
En complément sont données les notions de base en navigation aérienne et maritime.
Les annexes scientifiques sont plutôt réservées au physicien ou au météorologue.
Notations de cette page :
- Les mots-clés ont leur première lettre indiquée en majuscule et sont définis dans le Lexique.
- Les auteurs cités sont mentionnés entre crochets sous la forme [AUTEUR Titre Page]. Voir Bibliographie.
Le Nuage a toujours pour origine le refroidissement d'une masse d'air humide.
L'air atmosphérique contient en effet une quantité variable de vapeur d'eau (entre 0,1 % et 4 % en volume) issue de l'évaporation des océans, mers, lacs et sols humides.
Le contact entre une masse d'air chaud et une masse d'air froid entraîne alors la condensation de la vapeur d'eau contenue dans l'air chaud et la formation de Nuages.
Un air humide se compose d'air sec et d'eau, l'eau étant sous forme de gaz (vapeur d'eau) et aussi, à saturation, sous forme liquide (goutte d'eau en suspension) ou solide (cristaux de glace).
La quantité de vapeur d'eau contenue dans l'air atmosphérique possède un maximum fonction de la température et de la pression locale. Lorsque ce maximum est atteint (seuil de saturation), la vapeur d'eau retourne à l'état liquide (condensation) ou solide (cristallisation). Ainsi, à 20 °C et au niveau de la mer, l'air peut contenir environ 18 grammes d'eau par mètre cube avant de saturer. A 60 °C et au niveau de la mer, l'air sature dès 129 g/m3. A 20 °C et à 5500 m d'Altitude, l'air sature dès 9 g/m3.
Dans le domaine de la météorologie ou de la physique, le Taux de saturation (appelé aussi Humidité relative ou Degré hygrométrique) se mesure selon une échelle de 0 % à 100 %. La plage de bien-être pour les êtres humains se situe entre 45 et 65 %. En dessous, l'air est trop sec. Au-dessus, l'air est trop humide. A partir de 100 %, l'air est saturé de vapeur d'eau qui se condense alors en Brouillard, rosée ou givre.
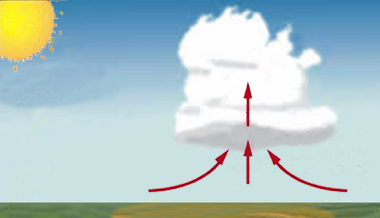



Il existe différents modes de refroidissement à l'origine de la formation des Nuages, d'origine thermique ou dynamique (cf [Météo-France, Comment se forme un nuage]) :
1. La convection ou convection verticale (voir Figure 1 ci-dessus) : l'air froid présent au niveau d'un sol chaud se réchauffe et se dilate. Plus léger, il monte dans l'atmosphère dont la pression décroît systématiquement avec l'altitude. L'air se refroidit alors par détente (à raison de presque 1 °C tous les 100 mètres) jusqu'au point de condensation de la vapeur d'eau sous forme de Nuages de convection, fréquents l'été sur terre et l'hiver au-dessus de la mer.
2. Le refroidissement par la base ou advection ou convection horizontale (voir Figure 2 ci-dessus) : lorsqu'une masse d'air doux circule au-dessus d'une surface plus froide, se forment des Nuages bas ou du Brouillard. C'est le cas notamment, l'hiver, lorsque de l'air doux de la mer arrive sur les eaux froides du continent. En été également, lorsque l'air doux du continent arrive sur les eaux froides de la mer.
3. Le soulèvement orographique (voir Figure 3 ci-dessus) : lorsqu'une masse d'air est poussée par le Vent vers un Relief, elle est contrainte de s'élever le long de la pente. En prenant de l'altitude, elle subit une détente et se refroidit. Un Nuage se forme alors sur le versant "au vent" et se dissipe sur le versant "sous le vent". Le type de Nuage dépend de la stabilité de l'air et de sa teneur en humidité. Une fois le sommet franchi, l'air, allégé d'une bonne partie de sa vapeur d'eau, subit au contraire une compression en dévalant la pente et se réchauffe (effet de Foehn).
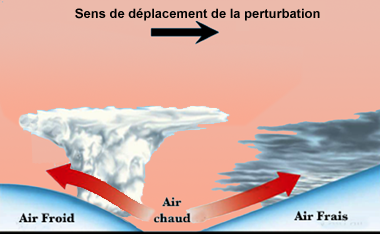
4. Le soulèvement frontal (voir Figure 4 ci-dessus) : dans une Perturbation en mouvement (Dépression dynamique), à l'interface chaud/froid entre deux masses d'air, l'air chaud se soulève au-dessus de l'air froid antérieur (Front chaud) et est rejeté en altitude par la progression plus rapide de l'air froid postérieur (Front froid). L'air chaud se refroidit en altitude et donne naissance à des Nuages le long des Fronts. Voir détail du processus ci-dessous (cyclogénèse).
La Pluie se délenche ensuite lorsque les gouttelettes en suspension dans le Nuage deviennent trop lourdes pour être soutenues par le courant ascendant.
Dans le cas où la Dépression n'est pas thermique mais due à la circulation atmosphérique elle-même (Dépression dynamique), l'école norvégienne de météorologie a élaboré en 1919 un modèle idéalisé de formation, maturation et mort des Dépressions des Latitudes moyennes qui est le suivant (cf [Wikipedia, Cyclogénèse]) :
1. Condition initiale : Deux masses d'air de température et d'humidité différentes se croisent sans aucun échange thermique (Front stationnaire souvent immobile).
2. Naissance (voir Figure 5 ci-dessus) : Une Perturbation thermique ou dynamique de l'atmosphère passant dans le secteur va alors induire un point d'inflexion appelé vague. Un petit centre de basse pression (Dépression) apparaît alors à la crête de la vague qui va initier une circulation cyclonique, c'est-à-dire que la rotation amène l'air doux de la masse chaude vers les Pôles et l'air froid vers l'Equateur quel que soit l'hémisphère.
3. Développement (voir Figures 6 et 7 ci-dessus) : Le Front stationnaire se transforme alors en deux Fronts distincts, le Front chaud et le Front froid, séparés par un Secteur chaud, et situés dans le quadrant sud de la Dépression (pour l'hémisphère nord). Les deux Fronts s'incurvent progressivement de plus en plus dans la direction de leur progression, comme les voiles d'un bateau.
4. Mort (voir Figure 8 ci-dessus) : Le Front froid, se déplaçant plus vite que le Front chaud, finit par le rejoindre (front occlus). L'air chaud est alors rejeté en altitude et se découple progressivement de la Dépression qui se dissipe naturellement par manque d'apport en air chaud. L'Occlusion a disparu et le Front stationnaire initial reprend progressivement ses caractéristiques d'origine.
Bien que dépassé à ce jour, le modèle norvégien reste valide pour des environnements atmosphériques diffluents (correspondant à une déformation du champ de pression sans mouvement vertical de l'air).
La cyclogénèse tropicale est par contre très différente de ce modèle. Elle est due à la convection profonde d'une masse d'air homogène, dont le déclencheur est la température de la mer.
Historiquement, la classification des Nuages a fait l'objet de deux systèmes de classification : celle du zoologue français J.B. de Lamarck (1744-1829) et celle du pharmacien londonien L. Howard (1772-1829) qui présentèrent des systèmes de classification presque identiques. Mais seul celui de Howard fut retenu car les noms y étaient mentionnés en latin.
Depuis, cette classification n'a subi que quelques perfectionnements et sert toujours de base pour l'Atlas International des Nuages, publié par l'Organisation Météorologique Mondiale émanant de l'ONU (voir [OMM Accueil] en Bibliographie).
La classification internationale des Nuages repose sur l'existence de Familles, de Genres, d'Espèces et de Variétés.
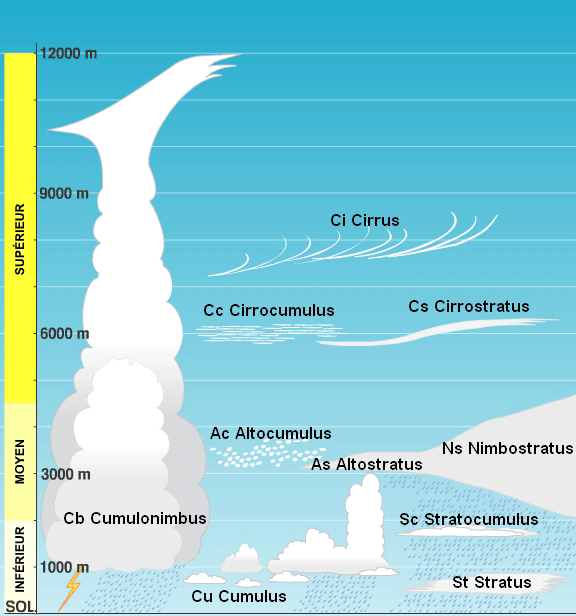
La Famille correspond à l'Altitude de la base du Nuage par rapport au sol. Pour les latitudes tempérées, les Altitudes sont les suivantes :
- Etage élevé (ou supérieur), entre 5 et 12 km d'altitude (préfixe "Cirro-", abréviation "C"),
- Etage moyen, entre 2 et 5 km d'altitude (préfixe "Alto-", abréviation "A"),
- Etage bas (ou inférieur), entre 0 et 2 km d'altitude (préfixe "Strato-", abréviation "S"),
- Multi-étage pour les Nuages à grand développement vertical (préfixe "Nimbo-", abréviation "N").
Le Genre correspond à la forme générale du Nuage (cf [HACKEL]) :
- cirrus (abréviation "Ci") pour les Nuages en Voile, correspondant à des nuages à contour flou et généralement isolés dans le ciel.
- stratus (abréviation "s" ou "St") pour les Nuages en Couche (ou nappe), correspondant à des nuages à texture uniforme et couvrant généralement la totalité du ciel.
- cumulus (abréviation "c" ou "Cu") pour les Nuages en Amas, correspondant à des nuages à contour net généralement arrondi, isolés ou regroupés dans le ciel.
Les Nuages en Voile et en Couche se forment par soulèvement le long des Fronts chauds.
Les Nuages en Amas se forment par convection ou par soulèvement le long des Fronts froids.
Le nom du Genre est composé de deux parties : l'étage et la forme. Ainsi, un Stratocumulus est un Nuage en Amas de l'étage bas, et son abréviation est "Sc".
Il y a quelques exceptions de nommage :
- le Cirro-cirrus s'appelle plus simplement Cirrus (abréviation "Ci").
- le Strato-stratus s'appelle plus simplement Stratus (abréviation "St").
- les Cumulus de l'Etage bas s'appellent Stratocumulus (abréviation "Sc") lorsque formés par convection horizontale et plus simplement Cumulus (abréviation "Cu") lorsque formés par convection verticale, les Cumulus se situant toujours en dessous des Stratocumulus (cf [BOUTELOUP]).
- le Nimbo-cumulus s'appelle au contraire Cumulonimbus (abréviation "Cb").
Au total, la classification comporte donc 10 Genres de Nuages (voir Figure ci-dessus).
Chaque Genre est divisé ensuite en un nombre d'Espèces et de Variétés (ou sous-espèces), dont le nom suit celui du Genre (voir [OMM Classification] en Bibliographie). Ainsi, un Altostratus translucidus est un Nuage en Couche de l'étage moyen à travers lequel on peut encore voir le Soleil. Les noms d'Espèces et de Variétés ont également leurs abréviations (en général, les trois premières lettres du nom). Exemples : "neb" pour nebulosus, "tr" pour translucidus.
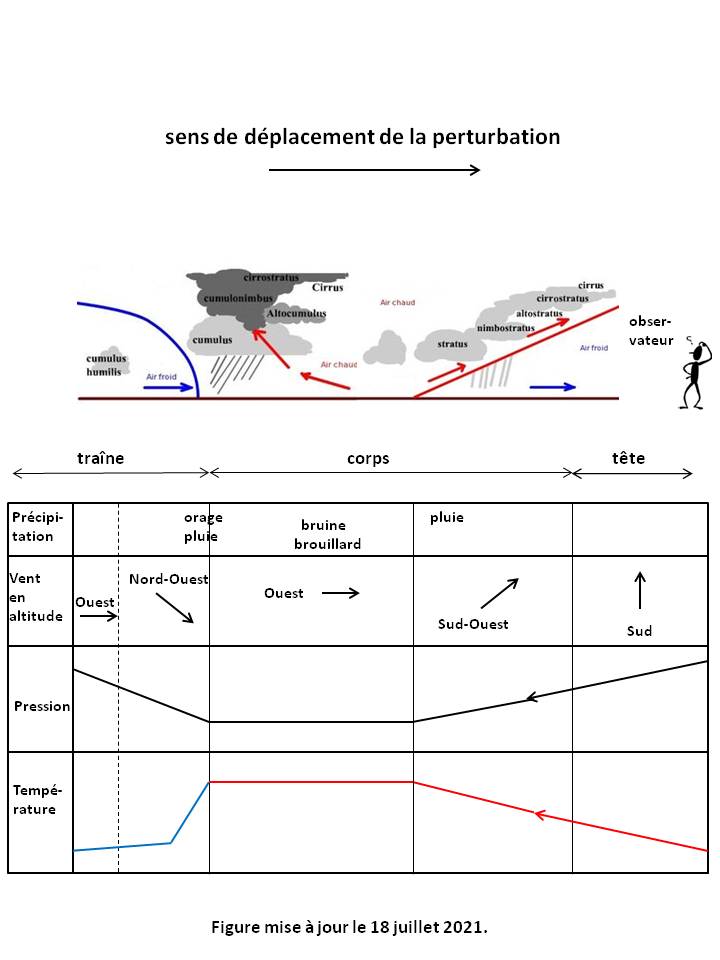
Une Perturbation atmosphérique se compose de trois parties (cf [Culture maritime][FONS][KOHLER) :
- la tête : elle est située à l'avant du Front chaud (ligne droite en rouge sur la Figure ci-dessus) et se caractérise par des Nuages élevés. Au passage de la Perturbation, on observe d'abord des Cirrus puis des Cirrostratus et/ou Cirrocumulus.
- le corps : il englobe le Front chaud et le secteur d'air chaud compris entre les deux Fronts. Il se caractérise par des Nuages épais et des Précipitations. On observe d'abord des Altostratus et/ou Altocumulus, associés à des Stratocumulus apportant la Pluie. Arrivent ensuite les Nimbostratus qui intensifient les Précipitations. Au passage du Secteur chaud, s'établit ensuite une certaine accalmie sous forme de Bruine ou de Brouillard.
- la traîne : elle englobe le Front froid (ligne courbe en bleu sur la Figure ci-dessus) et se caractérise par des Orages et des Précipitations à nouveau. On observe d'abord des Cumulonimbus provoquant des Orages, puis des Cumulus et/ou Stratocumulus apportant la Pluie.
La Perturbation est passée lorsque l'air chaud se trouve suffisamment rejeté en altitude par l'avant et par l'arrière et que les masses d'air froid se rejoignent au sol.
A noter que le Relief peut modifier la trajectoire des Fronts.
A noter également que la direction et la vitesse de déplacement des Nuages non orographiques constituent une bonne approximation de la Direction et de la Vitesse des Vents en altitude.
|
En synthèse du Tableau ci-dessous, on peut retenir que le temps prévisible par les Nuages sur 24 heures est globalement le suivant (cf [KOHLER][HACKEL]) : Nuages annonçant l'Orage : - Nuages en forme de montagne : Cumulus congestus  ou Cumulonimbus ou Cumulonimbus  . .- Nuages en petits moutons (type floccus)  , en créneaux (type castellanus) , en créneaux (type castellanus)  ou en rouleau horizontal (type volutus) ou en rouleau horizontal (type volutus)  . .- Nuages évolutifs en forme : grands Nuages noirs ou gris qui s'assemblent par nappes. - Nuages évolutifs en position : Nuages d'Orage se déplaçant dans la direction de l'observateur (voir Evolution des nuages). - Augmentation du degré hygrométrique de l'air. - Baisse de la pression atmosphérique, ressentie notamment par une odeur d'ozone (proche de celle de l'eau de javel) formée par les éclairs et rabattue au sol par le vent. Nuages annonçant la Pluie : - Nuages en forme de montagne : Cumulus congestus  ou Cumulonimbus ou Cumulonimbus  . .- Nuages en petits moutons (type floccus)  . .- Nuages produits par l'homme (type Cirrus homogenitus)  lorsqu'un avion à réaction produit une traînée de condensation durable (10 mn) et s'élargissant, signe d'un air très humide à haute altitude. lorsqu'un avion à réaction produit une traînée de condensation durable (10 mn) et s'élargissant, signe d'un air très humide à haute altitude.- Tous les Nuages en Couche : Cirrostratus, Altostratus, Stratus ou Nimbostratus. Voir Tableau ci-dessous. - Nuages évolutifs en forme : Nuages dont la base s'abaisse. - Nuages évolutifs en position : Nuages de Pluie se déplaçant dans la direction de l'observateur (voir Evolution des nuages). - Augmentation du degré hygrométrique de l'air. - Baisse de la pression atmosphérique, ressentie notamment par une odeur âcre (méthane et autres gaz) se libérant des feuilles en décomposition dans les zones boueuses (étangs, fossés, gouttières,etc.). Tous les autres Nuages annoncent en général du beau temps. |
Le Tableau ci-dessous permet de prévoir avec une bonne certitude les modifications du temps sur 24 heures (Orage, Pluie ou beau temps) en observant la forme des Nuages.
Légende du Tableau :
- La colonne 'Forme' correspond à la forme du Nuage (cf [HACKEL]) : Voile, Couche ou Amas.
- La colonne 'Abrévation' est l'abréviation officielle du nom pour le Genre de Nuage.
- La colonne 'Genre' est le nom officiel pour le Genre de Nuage. Pour une Forme donnée, les Genres sont listés verticalement par Etages décroissants (Cirro-, Alto-, Strato- puis Nimbo-).
- Les deux colonnes 'Photos' et 'Espèces/Variétés' illustrent les Espèces et Variétés fréquentes de Nuages, porteuses d'Orage ou de Pluie (Photos 1) ou porteuses de beau temps (Photos 2).
| Forme | Abréviation | Genre | Photos 1 | Espèces/Variétés fréquentes et porteuses d'Orage ou de Pluie | Photos 2 | Espèces/Variétés fréquentes et porteuses de beau temps |
|---|---|---|---|---|---|---|
| Voile | Ci | Cirrus |   | floccus (en petits moutons) → Orage ou Pluie homogenitus (produit par l'homme) avec traînée de condensation durable (10 mn) et s'élargissant → Pluie |     | uncinus (en virgule ou griffe) fibratus (en filaments) spissatus (dense) radiatus (rayonnant) |
| Couche | Cs | Cirrostratus |   | fibratus (en filaments) → Pluie nebulosus (nébuleux) → Pluie | ||
| Couche | As | Altostratus |      | opacus (opaque) → Pluie undulatus (onduleux) → Pluie duplicatus (multi-couches) → Pluie radiatus (rayonnant) → Pluie translucidus (translucide) → Pluie | ||
| Couche | St | Stratus |   | fractus (en morceaux) → Bruine nebulosus (nébuleux) → Bruine | ||
| Couche | Ns | Nimbostratus |  | nuage multi-étages gris et opaque → Pluie | ||
| Amas | Cc | Cirrocumulus |  | floccus (en petits moutons) → Orage ou Pluie |   | undulatus (onduleux) lacunosus (en nid d'abeille) |
| Amas | Ac | Altocumulus |    | floccus (en petits moutons) → Orage ou Pluie castellanus (en créneaux) → Orage volutus (en rouleau horizontal) → Orage |      | lenticularis (lenticulaire) translucidus (translucide) stratiformis (en rouleaux ou galets) opacus (opaque) mamma (mamelonné) |
| Amas | Sc | Stratocumulus |    | floccus (en petits moutons) → Orage ou Pluie castellanus (en créneaux) → Orage volutus (en rouleau horizontal) → Orage |  | stratiformis (en rouleaux ou galets) |
| Amas | Cu | Cumulus |  | congestus (bourgeonnant) → Orage ou Pluie |    | humilis (petit) mediocris (moyen) fractus (en morceaux) |
| Amas | Cb | Cumulonimbus |     | nuage multi-étages gris et en forme de montagne : calvus (chauve) → Orage capillatus (chevelu) → Orage incus (en enclume) → Orage mamma (mamelonné) → Pluie |
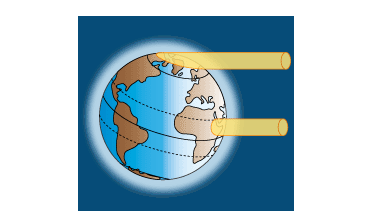
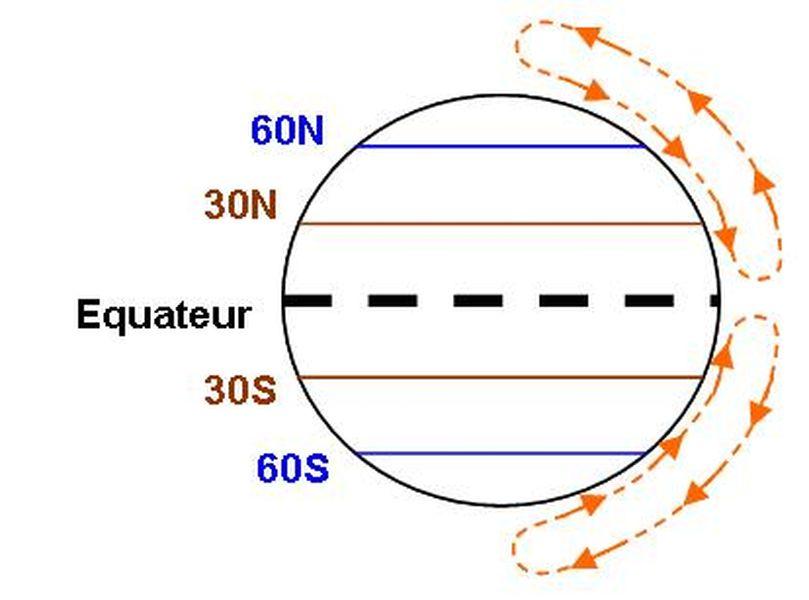
Le rayonnement solaire arrive sur Terre sous forme d'un faisceau parallèle. La Terre étant sphérique, la puissance solaire reçue par unité de surface terrestre n'est pas égal sur toutes les Latitudes (voir Figure 1 ci-dessus) et le globe terrestre se découpe en trois zones climatiques. Aux Pôles se trouvent les zones polaires, où la température est la plus basse. La zone chaude est située autour de l'Equateur et la zone intermédiaire correspond à la zone tempérée. Cette différence de température entre l'Equateur et les Pôles fait que l'air froid tend à se déplacer vers l'Equateur et l'air chaud vers les Pôles (voir Figure 2 ci-dessus).
Le Vent a donc pour origine une différence de température, donc de pression, entre deux masses d'air voisines, ce qui caractérise deux types de Vent (cf [Météo-Contact]) :
- Le Vent vertical est le Vent perpendiculaire à la surface de la Terre, provoqué principalement par une différence de température entre une masse d'air et un objet situé dessous (océan ou sol),
- Le Vent horizontal est le Vent parallèle à la surface de la Terre, provoqué principalement par une différence de pression entre deux masses d'air voisines.
Ce sont donc des déformations thermiques qui contribuent principalement à la formation des Vents verticaux (cf [Météo-Contact]) et des déformations dynamiques pour les Vents horizontaux (cf [BISSEK, p.113]).
A l'échelle planétaire, les Vents verticaux sont de faible intensité (de l'ordre de 1 à 10 cm/s) alors que les Vents horizontaux sont de l'ordre de 1 à 10 m/s. C'est pourquoi l'étude du mouvement des masses d'air dissocie les deux vecteurs Vitesse.
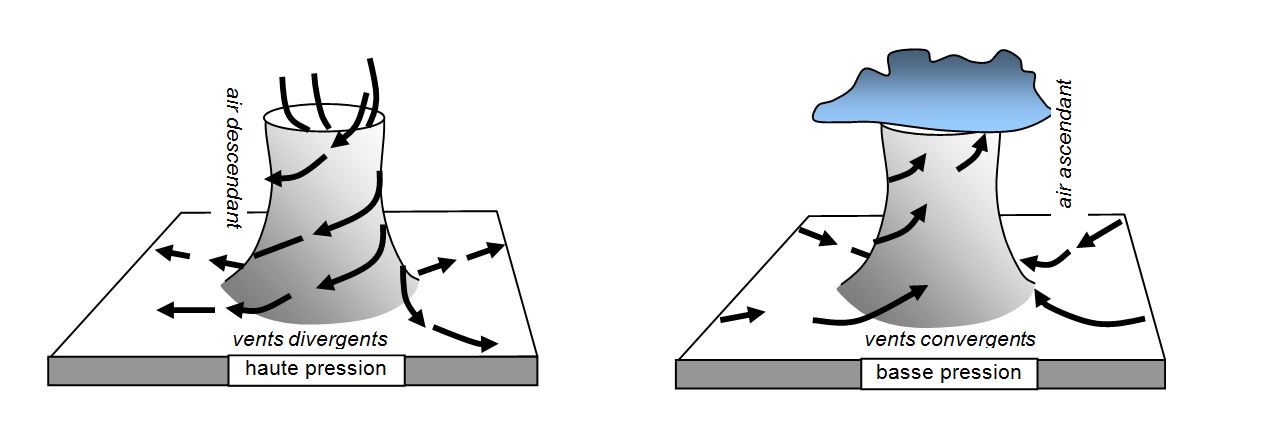

Les Centres d'action commandent la circulation des Vents et le mouvement des Perturbations atmosphériques au-dessus des étendues qu'ils surplombent et avoisinent. Ils sont directement liés aux mouvements verticaux des vents planétaires à basse altitude (cellules de Hadley, Ferrel et polaire). D'une manière générale, les Centres d'action maritimes sont permanents, les continentaux sont semi-permanents. En fonction des saisons, ils peuvent gonfler ou se résorber, voire disparaître.
Un Centre d'action est un Anticyclone ou une Dépression agissant sur une grande étendue, dont l'origine peut être thermique (voir Figures 1 et 2 ci-dessus) ou dynamique, et dont la durée de vie est variable (cf [Wikipedia, Anticyclone][Wikipedia, Dépression]).
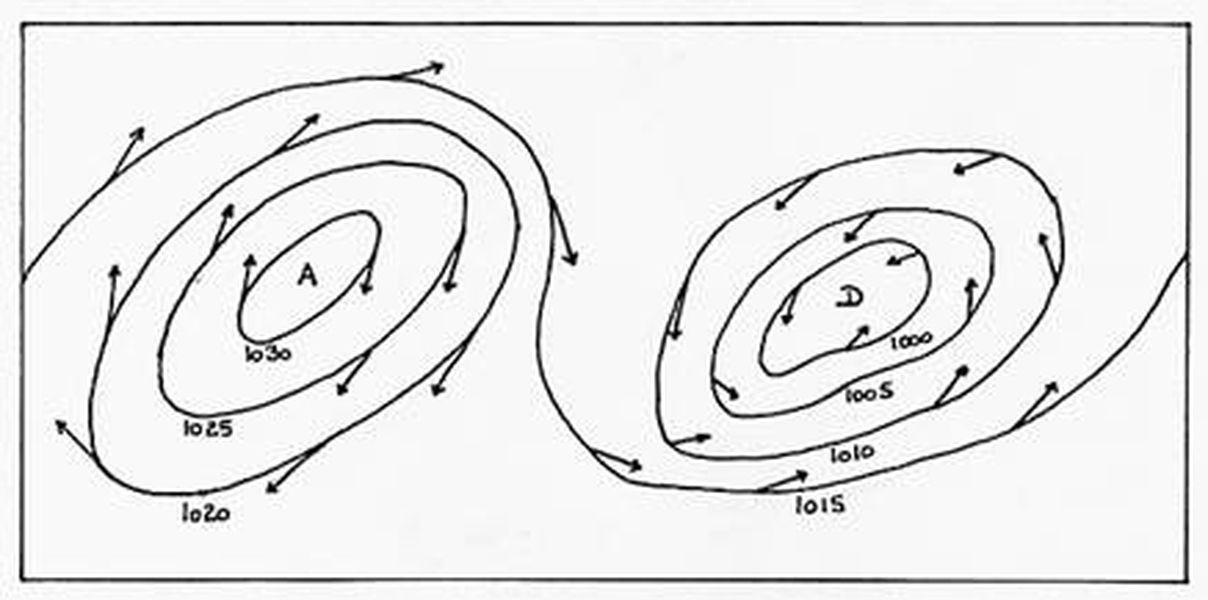
Les lignes reliant les points d'égale pression entre les Centres d'action s'appellent les Isobares. Ils sont l'équivalent des courbes de niveau topologique (courbe d'altitude) dans les cartes géographiques. Par endroits, les Isobares se referment sur eux-mêmes et délimitent ainsi les Centres d'action (voir Figure 3 ci-dessus).
En France métropolitaine, les principaux Centres d'action sont les suivants (cf [MARTIN, pp 68-69]) :
- Au sud-ouest, l'Anticyclone des Açores apporte de l'air tropical humide et tiède.
- Au nord-ouest, la Dépression d'Islande apporte de l'air polaire humide et froid.
- A l'est, l'Anticyclone russo-sibérien apporte de l'air polaire sec et froid.
- Au sud, l'Anticyclone saharien apporte de l'air tropical chaud, sec ou humide.
Des Reliefs importants (Pyrénées, Alpes, Massif Central, Jura, Vosges) séparent alors les zones d'influence de ces Centres d'action en quatre climats types :
- Au nord de la Loire : climat océanique à l'ouest, continental à l'est ;
- Au sud de la Loire : climat océanique à l'ouest, montagnard et méditerranéen au sud-est.
Des sous-climats montagnards et une foule de microclimats locaux résultent de ces climats types.
Ainsi, en France métropolitaine, le temps est particulièrement instable, régi soit par des conditions anticycloniques calmes et sèches qui provoquent souvent des vagues de froid ou de sécheresse, soit par des successions de Perturbations Frontales venteuses et pluvieuses qui évoluent souvent en Tempêtes, voire parfois en Ouragans.
Les Centres d'action ne sont pas statiques. Ils peuvent se déplacer (par exemple, circulation d'ouest en est de l'Atlantique vers l'Europe) et se déformer (une Dépression "se creuse" ou "se comble", un Anticyclone "gonfle" ou "s'affaisse"). Leur durée de vie est limitée : quelques jours pour une Dépression, deux ou trois semaines pour un Anticyclone (cf [Meteo-pro, Comment]).
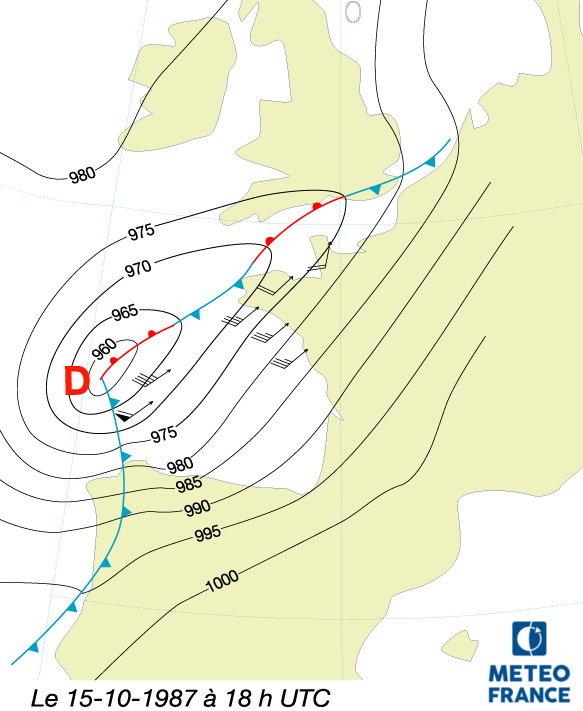
Les Figures 6 et 7 ci-dessus montrent en exemple le déplacement et la déformation d'une Dépression lors de "l'Ouragan" du 15 au 16 octobre 1987 qui a touché le quart nord-ouest de la France métropolitaine (cf [Météo-France, Tempêtes]) :
- Le 15 octobre à 18h UTC (voir Figure 6), la première Dépression à 970 hPa touche Ouessant avec seulement quelques rafales de vent.
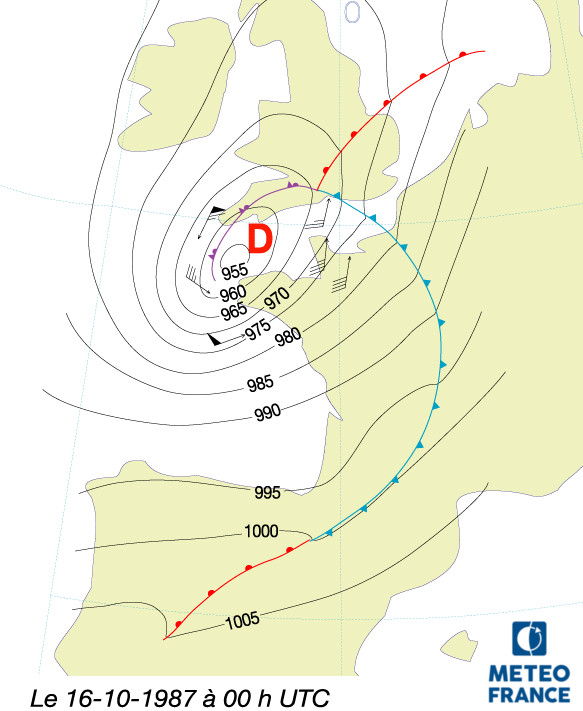
- Le 16 octobre à 00h UTC (voir Figure 7), la seconde Dépression frôle Ouessant avec une pression de 955 hPa et une pic de Vent à 216 km/h en Pointe du Raz. Elle traverse ensuite l'Angleterre durant la nuit, poursuit sa trajectoire vers le nord dans la journée du 16 octobre tout en se comblant progressivement.
Le Vent vertical a pour origine un Centre d'action, Anticyclone ou Dépression (cf [Wikipedia, Anticyclone][Wikipedia, Dépression]).
Les Anticyclones sont principalement caractérisés par un lent mouvement vertical descendant de l'air qui augmente sa pression sur le sol, et les Dépressions par un mouvement vertical ascendant de l'air qui diminue sa pression en altitude.
En théorie, si la Terre était immobile dans l'espace, le Vent en altitude ne subirait que deux forces principales (pesanteur et forces dues au gradient de pression) et se déplacerait de manière rectiligne depuis un centre de haute pression (Anticyclone) vers un centre de basse pression (Dépression) en soufflant perpendiculairement aux Isobares, comme l'eau dévale la pente d'une colline. Mais en réalité, le mouvement du Vent horizontal par rapport à la surface de la Terre est perturbé par cinq facteurs (cf [DE PARCEVAUX][SciencePost][Gouvernement du Canada, METAVI]) :
1. La rotation terrestre qui crée deux forces d'inertie virtuelles. La première est la force d'entraînement (ou force centrifuge globale) qui est englobée dans la force de gravité. La seconde est la force de Coriolis qui modifie le Vent en Direction et fait souffler le Vent parallèlement aux Isobares (vent géostrophique). Dans l'hémisphère nord, la force de Coriolis est dirigée vers la droite, le Vent laissant les basses pressions à sa gauche (règle de Buys-Ballot) de sorte qu'il tourne autour d'un Anticyclone dans le sens horaire et autour d'une Dépression dans le sens anti-horaire (voir Figure 3 ci-dessus). Dans l'hémisphère sud, c'est le contraire. A l'Equateur, la force d'inertie de Coriolis est quasi-nulle et d'autres facteurs interviennent pour déterminer la Direction du vent (voir Equation du vent géostrophique).
2. La courbure des Isobares qui crée une force centrifuge locale, laquelle n'est à considérer que pour des Vents à grande Vitesse suivant des Isobares fortement courbés (par exemple autour de Dépressions très intenses) ou pour des Vents en zone équatoriale pour laquelle la force d'inertie de Coriolis est quasi-nulle (voir Equation du vent géostrophique).
3. L'action des Reliefs importants (montagnes, vallées, etc.) qui contrarient ou au contraire canalisent le Vent.
4. L'action des faibles Reliefs (mers, plaines, plateaux, etc.) qui crée une force de friction à grande échelle au niveau du sol et dans la Couche limite atmosphérique. Cette force modifie le Vent en Direction et en Vitesse (voir Equation du vent synoptique - Prise en compte de la friction). Au-dessus de la Couche limite atmosphérique, les vents sont approximativement Géostrophiques.
5. Le contraste thermique entre deux Reliefs voisins qui produit un Vent local par convection verticale ou horizontale.
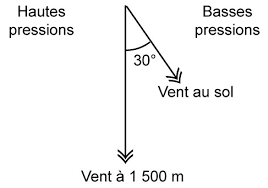
En Direction, le Vent au sol est dévié par rapport aux Isobares d'un certain angle en rentrant dans la Dépression et aussi en sortant de l'Anticyclone (voir Figure 3 ci-dessus). Pour un Vent au sol sans Reliefs importants, cet angle est d'environ 30° sur terre et 15° sur mer (cf [IRM][CIRAS]). Dans l'hémisphère nord, la déviation se fait sur la gauche (voir Figure 5 ci-dessus). Dans l'hémisphère sud, c'est le contraire.
En Vitesse, le Vent au sol est diminué par rapport au Vent en altitude, en général de 30 %.
La règle ou loi de Buys-Ballot est la suivante. Dans l'hémisphère nord, quand on se place face au Vent, la Dépression est toujours à droite (voir Figure 4 ci-dessus). Dans l'hémisphère sud, c'est le contraire.
Avant l'arrivée de la radio, cette règle était le seul moyen, avec l'observation des Nuages, de prévoir le temps en mer. Les navigateurs évitaient ainsi les Tempêtes et utilisaient au mieux les Vents.
On distingue quatre grandes familles de Vents (cf [Météo 45][UAMOB][Gouvernement du Canada, METAVI]) :
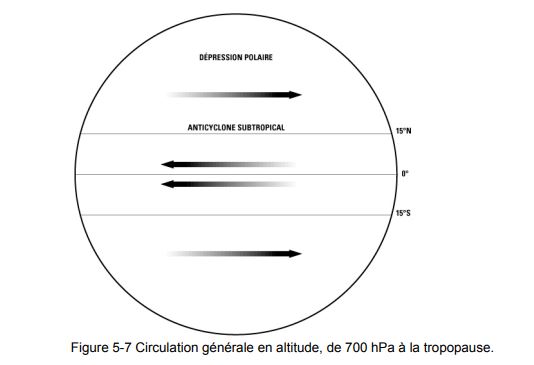
Les vents planétaires à haute altitude sont situés à plus de 3000 m d'altitude (correspondant à 700 hPa) et vont jusqu'à la tropopause. On distingue :
- Les courants orientaux : situés à 5000 m d'altitude, ils se déplacent d'est en ouest, dans la zone intertropicale.
- Les courants occidentaux : situés à 5000 m d'altitude, ils se déplacent d'ouest en est, au nord du Tropique du Cancer et au sud du Tropique du Capricorne, y compris dans les zones polaires.
- Les courants-jets (jet stream en anglais) : provenant des courants occidentaux, ce sont des mouvements d'air très rapides pouvant atteindre 100 m/s. Situés entre 6000 et 12000 m d'altitude, ils ont une trajectoire sinusoïdale entre les zones de Dépression et celles d'Anticyclone de même Latitude. Existent le subtropical (entre les 25e et 30e Parallèle) et le polaire (entre les 45e et 60e Parallèle). Ils peuvent changer de Direction en cours d'année et sont souvent responsables d'effets climatiques exceptionnels comme les vagues de froid et les canicules.
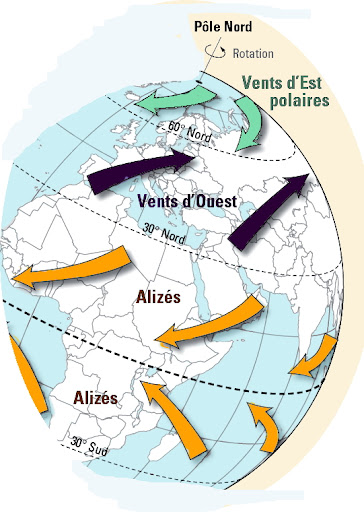
Les vents planétaires à basse altitude sont situés à moins de 2000 m d'altitude et sont fortement influencés par la rotation terrestre (force de Coriolis). On distingue :
- Les alizés (ou Vents d'est tropicaux) : situés entre l'Equateur et le 30e Parallèle (cellule de Hadley), ce sont des Vents d'est constants (20 km/h) qui se déplacent des zones subtropicales vers l'Equateur. Ils soufflent du nord-est dans l'hémisphère nord et du sud-est au sud de l'Equateur.
- Les Vents d'ouest tempérés : situés entre le 30e et le 60e Parallèle (cellule de Ferrel), leur mouvement est opposé à celui des alizés.
- Les Vents d'est polaires : situés entre le 60e Parallèle et le Pôle (cellule polaire), leur mouvement est dans la même Direction que celle des alizés et donc à l'opposé des Vents d'ouest.
Les perturbations cycloniques résultent de la rencontre de grands fronts chauds et froids à basse altitude. On distingue :
- Les moussons : Vents saisonniers des régions tropicales (océan indien et Asie du Sud), apportant de fortes Précipitations. Ils soufflent de la mer vers les côtes en été, et le contraire en hiver.
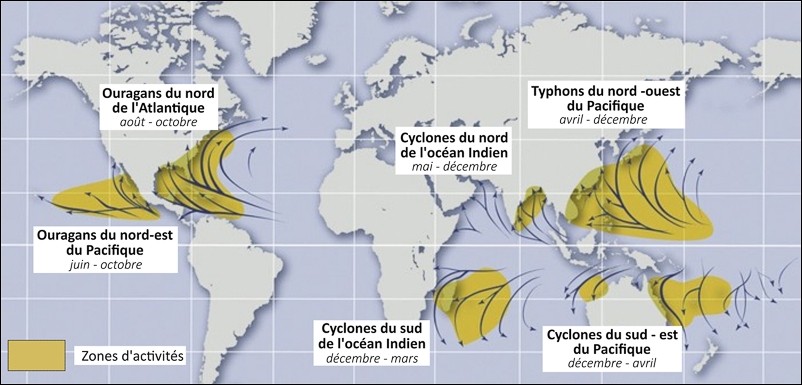
- Les cyclones : larges zones de Nuages Orageux en rotation accompagnées de Vents forts, qui se forment dans les océans. On distingue deux types de cyclone :
Cyclone tropical : situé entre les Tropiques. Appelé "Ouragan" dans l'Atlantique Nord et le Pacifique nord-est, "Typhon" en Asie de l'est et "Cyclone" dans les autres bassins océaniques.
Cyclone extratropical (ou cyclone des latitudes moyennes) : situé entre la ligne des Tropiques et le Cercle polaire.
Les vents régionaux et locaux couvrent des distances de moins de 500 km et sont dépendants du Relief comme suit :
- soit contrariés (*) ou au contraire canalisés (**) par les Reliefs importants (montagnes, vallées, etc.) ;
- soit seulement modifiés (***) par la friction sur les faibles Reliefs (mers, plaines, plateaux, etc.) ;
- soit produits localement par contraste thermique (****) entre deux Reliefs voisins.
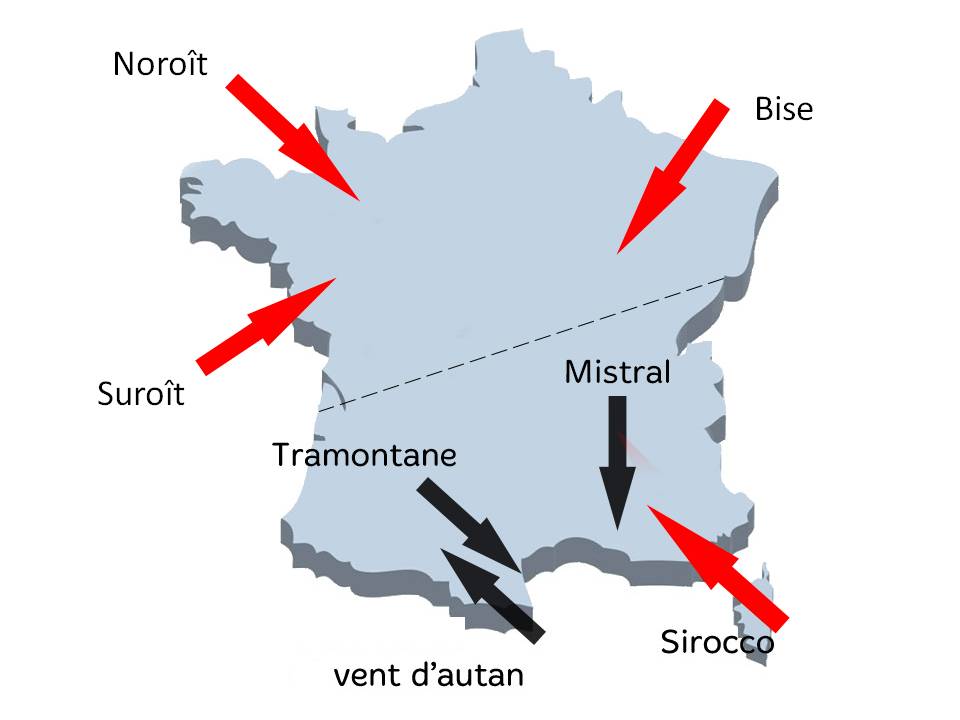
En France métropolitaine, on distingue les différents Vents principaux suivants (cf [Météo-France, Les vents régionaux]) :
(*) Le foehn : Vent sec et chaud dû à l'affaissement de l'air après le passage d'un Relief montagneux (Alpes et Pyrénées).
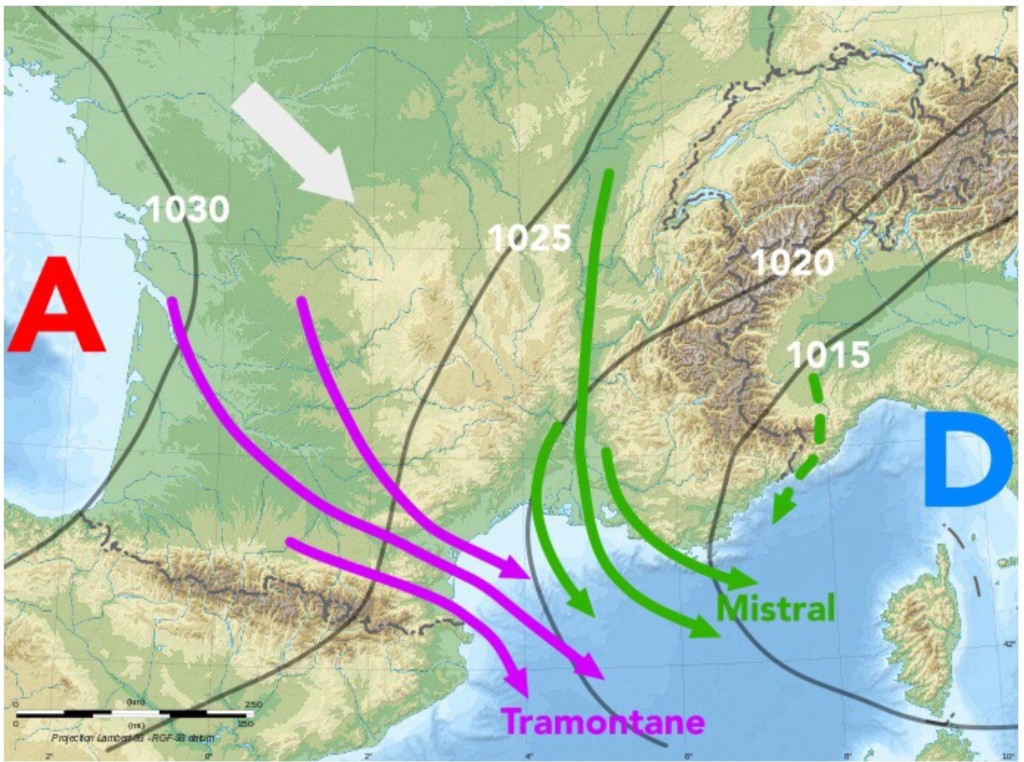
(**) La tramontane (ou cers dans le Lauragais) (voir Figure 2 ci-dessus) : Vent sec et froid de beau temps venant du nord-ouest et traversant les Pyrénées. Il indique la présence d'un Anticyclone centré sur l'Espagne et d'une Dépression centrée sur le Golfe de Gênes. Les masses d'air soufflent après le passage d'un front froid pluvieux qui atteint la Méditerranée après avoir parcouru du nord-ouest au sud-est l'ensemble de la France. Le Vent se renforce par effet venturi en passant dans le couloir entre les monts du sud du Massif Central et les contreforts des Pyrénées.
(**) Le mistral blanc (voir Figure 2 ci-dessus) : Vent sec et froid de beau temps venant du nord dans la vallée du Rhône, du nord-ouest dans la région marseillaise et de l'ouest sur la Corse. Il a la même cause météorologique que celle de la tramontane et diffère seulement du couloir montagneux utilisé : la vallée du Rhône. Existe également le mistral noir, Vent humide et froid de mauvais temps, qui se produit occasionnellement lorsque l'Anticyclone se prolonge en une dorsale qui transmet par le nord-ouest un flux d'air maritime, nettement plus humide que les flux habituels.
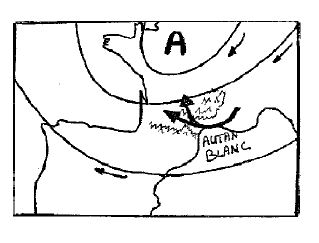
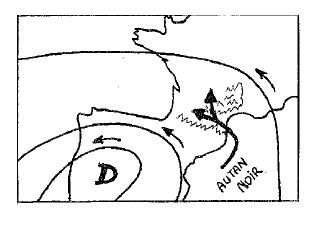
(**) L'autan (voir Figures 3 et 4 ci-dessus) : Vent venant du sud-est et traversant le Midi toulousain. On distingue deux types de Vents (cf [JAMME]). L'autan blanc est un Vent sec de beau temps, frais en hiver et doux en été, qui peut souffler pendant une semaine (voir Figure 3 ci-dessus). Il indique la présence d'un Anticyclone centré sur le Danemark. Les masses d'air viennent du continent et suivent le couloir du Lauragais. L'autan noir est un Vent humide et chaud de mauvais temps, qui souffle sur une à deux journées (voir Figure 4 ci-dessus). Il indique la présence d'une Dépression centrée sur l'Espagne. Les masses d'air le plus à l'est survolent la Méditerranée et se gorgent d'eau avant d'entrer dans le couloir du Lauragais.
(***) La bise blanche (voir Figure 5 ci-dessus) : Vent sec et froid de beau temps venant du nord et du nord-est, et traversant la Lorraine et la Savoie. Il indique la présence d'un Anticyclone centré sur le nord de l'Europe (Iles britanniques ou péninsule scandinave) associé parfois à une Dépression centrée sur le golfe de Gênes. Les masses d'air soufflent généralement après le passage d'un front froid pluvieux qui marque la fin d'une Perturbation. Existe également la bise noire, Vent humide et froid de mauvais temps, qui se produit occasionnellement lorsque l'influence dépressionnaire est prédominante.
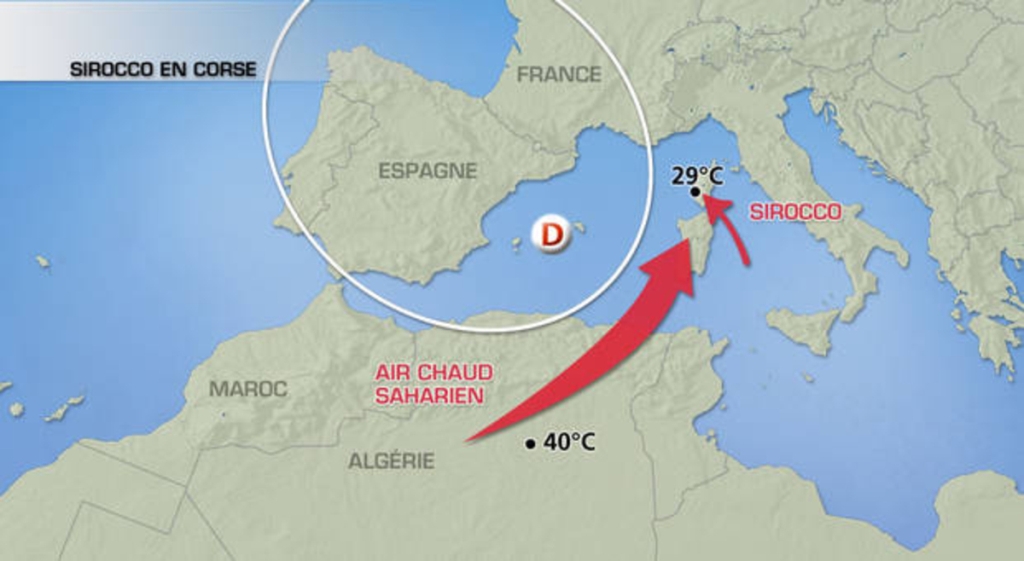
(***) Le sirocco (voir Figure 6 ci-dessus) : Vent venant du sud et du sud-est, et traversant la Corse (Vent sec et chaud) et la côte méditerranéenne (Vent humide et frais). Il indique la présence d'une Dépression centrée sur l'Espagne. Les masses d'air provenant de l'Anticyclone du Sahara traversent le nord de l'Afrique, contournent la Dépression par l'est et franchissent parfois la côte méditerranéenne pendant quelques heures sous forme d'un front chaud séparé (cf [PEDELABORDE]). Le sable transporté par le Vent augmente alors les risques de Brouillard et de Pluie, les particules de sable agissant comme des noyaux de condensation.
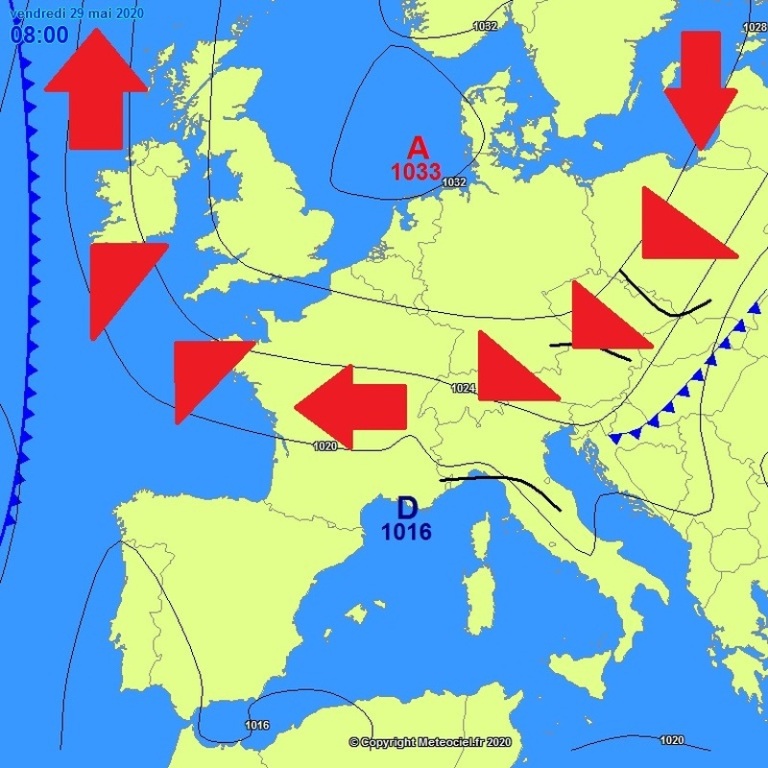
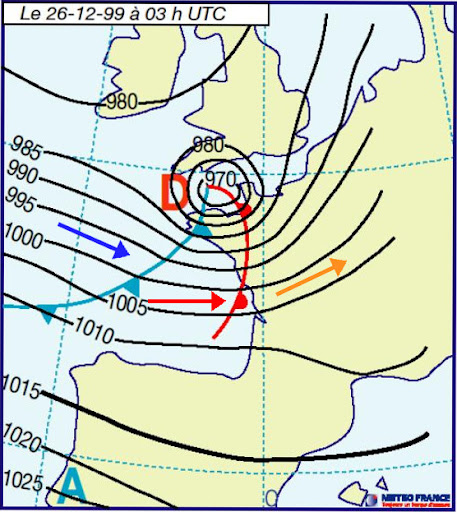
(***) Le suroît et le noroît (voir Figure 7 ci-dessus) : Vents venant de l'ouest et traversant la Normandie, la Bretagne et la côte atlantique. Les masses d'air soufflent entre la Dépression d'Islande et l'Anticyclone des Açores. Lors du passage de la Dépression dans son déplacement d'ouest en est, le Vent souffle du sud-ouest (suroît, humide et chaud, flèche orange sur la Figure) à l'avant du front chaud, d'ouest (flèche rouge) entre le front chaud et le front froid puis du nord-ouest (noroît, sec et froid, flèche bleue) à l'arrière du front froid.
(****) La brise : Vent léger local dû à un contraste thermique entre deux Reliefs voisins (brise de terre/mer, brise de pente montante/descendante, brise de vallée amont/aval). La Direction du Vent s'inverse entre le jour et la nuit.

Dans les deux hémisphères, aux latitudes moyennes où soufflent des Vents Dominants d'ouest (par exemple de l'Atlantique vers l'Europe), la Figure ci-dessus donne alors l'évolution du Vent en altitude au passage de la Perturbation atmosphérique (Dépression).
Est indiquée également l'évolution de la pression et de la température.
En synthèse, on peut retenir que, dans ces conditions (cf [KOHLER][FONS]) :
|
Concernant le Vent en altitude : - Le temps va s'aggraver lorsque le Vent "descend", c'est-à-dire quand il tourne dans le sens inverse des aiguilles d'une montre, en passant par exemple du nord au sud par l'ouest. - Dans la tête de la Perturbation, le Vent souffle du sud. En France métropolitaine, sur terre et sans Reliefs importants, cela correspond à un Vent au sol qui souffle du sud-est. - Dans le corps, le Vent se renforce progressivement et s'oriente au sud-ouest (vent de suroît). Dans le secteur d'air chaud, il souffle en général de l'ouest. - Dans la traîne, au passage du Front froid, le Vent vire brusquement au nord-ouest (vent de noroît) et se renforce. En fin de traîne, il souffle en général de l'ouest. Concernant la pression, elle baisse progressivement puis reste stable dans le secteur d'air chaud. Au passage du Front froid, la pression remonte rapidement puis se stabilise en fin de traîne. Concernant la température, elle monte progressivement puis reste stable dans le secteur d'air chaud. Au passage du Front froid, la température baisse brutalement avant de se stabiliser à la température de la masse d'air froid. |
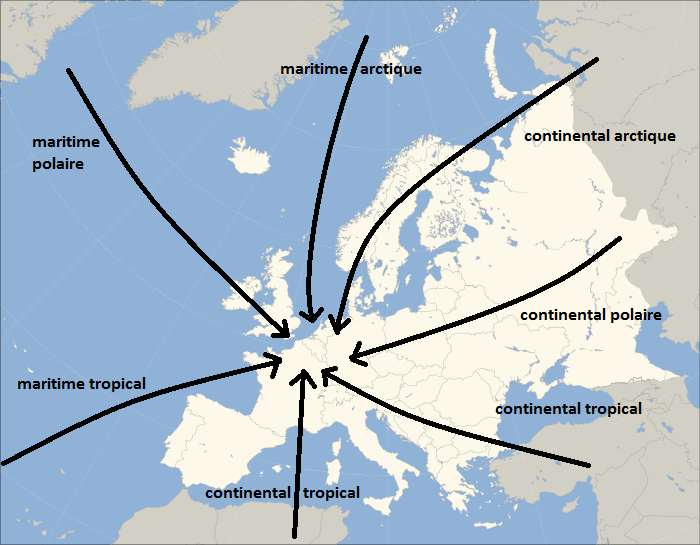
Les Vents en altitude correspondant aux masses d'air qui traversent la France métropolitaine sont les suivants (voir Figure ci-dessus) :
- Vent du nord (air maritime arctique) : Vent froid. Porteur d'Orage et de Pluie. Rare en été.
- Vent d'est et de nord-est (air continental polaire et arctique) : Vent froid en hiver et doux en été. Porteur de beau temps.
- Vent du sud et de sud-est (air continental tropical) : Vent chaud. Porteur d'Orage et de Pluie. Rare en hiver.
- Vent du sud-ouest (air maritime tropical) : Vent doux. Porteur de Pluie en hiver et de beau temps en été.
- Vent d'ouest et de nord-ouest (air maritime polaire) : Vent frais. Porteur de Pluie et de Bruine.
Direction du vent en altitude :
Pour déterminer la Direction du Vent en altitude, une méthode simple consiste à observer dans le ciel les Nuages les plus hauts en estimant leur direction (d'où ils viennent), par exemple avec une boussole en visant le Nuage par rapport à un point fixe tel un mât de drapeau ou une étoile.
Une autre méthode, utilisable dans le cas de faibles Reliefs, consiste à déterminer la Direction du vent au sol (voir ci-après) puis d'appliquer une correction : en France métropolitaine, sur terre, le Vent en altitude est décalé de 30° sur la droite par rapport au Vent au sol (voir Vent en altitude et vent au sol). Ainsi, un Vent au sol venant du sud-est (135°) correspond à un Vent en altitude venant presque du sud (165°).
Direction du vent au sol :
Pour déterminer la Direction du Vent au sol, existent deux méthodes simples et utilisables partout (cf [KOHLER][CIRAS]) :
- lever un doigt mouillé au-dessus de la tête et sentir le côté froid (dû à l'évaporation) ;
- pivoter lentement sur soi-même dans un endroit bien dégagé et sentir la Direction du vent sur le visage (dont la peau est sensible).
|
En synthèse, on peut retenir que, en France métropolitaine : Les Vents de mauvais temps sont (voir Classification) : - soit des Vents occasionnels et généralement de Direction constante par rapport au Relief (principalement le mistral noir, l'autan noir, la bise noire et le sirroco). - soit des Vents Dominants venant de l'ouest (le suroît et le noroît) et dont la Direction évolue en fonction du déplacement de la Dépression (voir Evolution des vents). Pour visualiser la Direction d'où souffle le Vent en altitude, lorsqu'on est sur terre et sans Reliefs importants, il faut pivoter SUR SA DROITE de 30° par rapport au Vent au sol arrivant en plein visage. Pour une prévision rapide et simplifiée, il suffit alors de retenir que, d'une façon générale (cf [KOHLER]) : - Le beau temps a pour origine une masse d'air continental, qu'elle soit polaire ou tropicale. Cela correspond à des Vents en altitude de secteur nord-est à sud. - Le mauvais temps a pour origine une masse d'air maritime, qu'elle soit polaire ou tropicale. Cela correspond à des Vents en altitude de secteur sud-ouest à nord. - Une masse d'air maritime tropical (secteur sud-ouest) peut cependant donner du beau temps, mais seulement en été. |

Pour bien lire une carte météo, il faut repérer dans l'ordre les éléments suivants (cf [KOHLER][IRM]) :
1- La date et l'heure
2- Les isobares
3- Les centres d'action
4- La direction du vent
5- La vitesse du vent
6- Les fronts météorologiques
7- Les dorsales, thalweg, cols et marais barométriques
Une carte météo décrit une situation météorologique à un instant précis.
La date et l'heure UTC sont toujours indiquées, généralement dans un coin de la carte.
L'heure UTC (Universal Time Coordinated) est l'heure de référence internationale (voir Relativité - Lexique - Temps standard). Elle correspond exactement à l'heure Z (Zulu Time ou Z Time), et aussi quasiment à l'heure GMT, parfois indiquées sur certaines cartes météo.
En France métropolitaine, pour connaître l'heure locale à partir de l'heure UTC, il faut donc rajouter une heure en hiver (heure CET : Central European Time) et deux heures en été (heure CEST : Central European Summer Time).
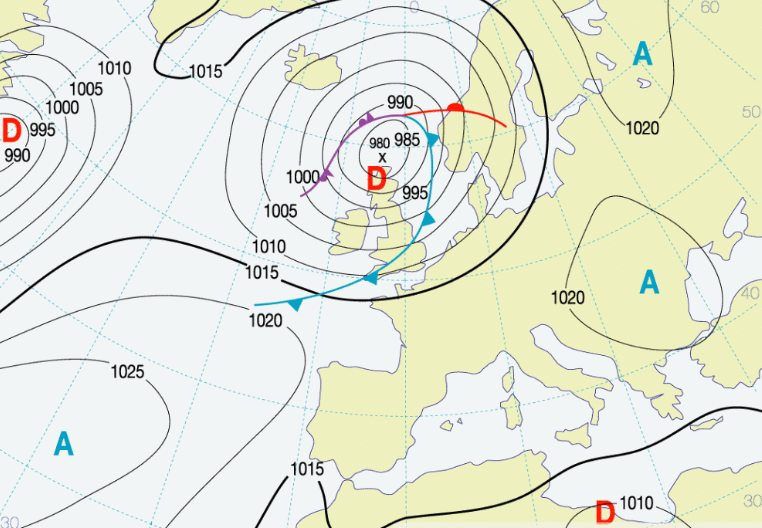
Sauf indication contraire (cas des cartes d'altitude), les Isobares sont indiqués sur des cartes normalisées au niveau de la mer, dites "cartes de surface" (voir Figure 1 ci-dessus).
Ils sont espacés par convention de 5 en 5 hPa (anciennement mbar) sur les cartes françaises et de 4 en 4 hPa sur les cartes anglaises.
L'Isobare de 1015 hPa correspondant à la pression atmosphérique standard apparaît généralement selon une ligne plus épaisse que les autres (voir Figure 1 ci-dessus).
Les centres d'action font partie des éléments les plus importants d'une carte météo car leur positionnement conditionne le temps qu'il fait (voir Formation des vents).
L'Anticyclone a pour abréviation A ((Anticyclone) ou H (Haute pression) en français, H en anglais (High) et H en allemand (Hoch).
La Dépression a pour abréviation D (Dépression) ou B (Basse pression) en français, L en anglais (Low) et T en allemand (Tief).
Sur les cartes en couleur, l'Anticyclone apparaît généralement en couleur bleue et la Dépression en couleur rouge.
Par exemple, en Europe occidentale, la Dépression est généralement centrée sur l'Islande et l'Anticyclone sur les Açores. Le Vent souffle ainsi en laissant la Dépression sur la gauche et prend la Direction de l'ouest (voir Figure 1 ci-dessus). Ce Vent est le flux Dominant d'ouest qui affecte la plupart du temps la France métropolitaine, à l'exception du pourtour méditerranéen.
Le Vent indiqué sur une carte météo de surface est le Vent au sol (vent synoptique).
La Direction du vent est représentée par une hampe de Vent (sauf pour un Vent calme de moins de 1 noeud, représenté par un cercle), dont la tête pointe dans la Direction d'où vient le Vent et dont l'autre extrémité touche le cercle de la station météo (voir Figure 2 ci-dessus). Cette Direction se mesure en degrés (de 0° à 360°) comptés dans le sens horaire et a pour référence :
- le Nord géographique dans les messages météo,
- le Nord magnétique dans les messages transmis par un organisme de circulation aérienne (tours de contrôle).
Sur les cartes Isobariques, la Direction du vent peut aussi se déduire des Isobares en tenant compte du sens de rotation des Vents autour des Centres d'action (voir Mécanisme de formation du vent horizontal) et de la déviation du Vent au sol (voir Vent en altitude et vent au sol).
Le Vent indiqué sur une carte météo de surface est le Vent au sol (vent synoptique).
La Vitesse du vent (ou "force" du vent) est représentée par une ou plusieurs barbules de Vent (fanions et/ou traits) posées sur la hampe et dirigées vers les basses pressions de la hampe : fanion (50 noeuds), trait (10 noeuds), demi-trait (5 noeuds), hampe seule (moins de 3 noeuds). Voir Figure 2 ci-dessus.
A noter que cette vitesse diminue au fur et à mesure que l'on s'approche du centre d'un Anticyclone. En mer, c'est idéal pour réparer son bateau mais problématique pour les skippers qui prennent soin de le contourner pendant une course.
Sur les cartes Isobariques, la Vitesse du vent peut aussi se déduire grossièrement du resserrement des Isobares. Ainsi, pour les Latitudes tempérées, moins de 100 km entre deux lignes Isobares est l'indice d'une forte Tempête.
Pour les régions hors zone équatoriale, on peut aussi utiliser la relation (R9) donnant le Vent en altitude (Vent géostropique) en fonction de la Latitude Φ et du gradient de pression |dp/dh| en mesurant perpendiculairement la distance (dh) entre deux Isobares proches (dp). Voir Equation du vent géostrophique. Ensuite, pour avoir la Vitesse du vent au sol, il faut tenir compte de l'atténuation du Vent au sol (voir Vent en altitude et vent au sol).
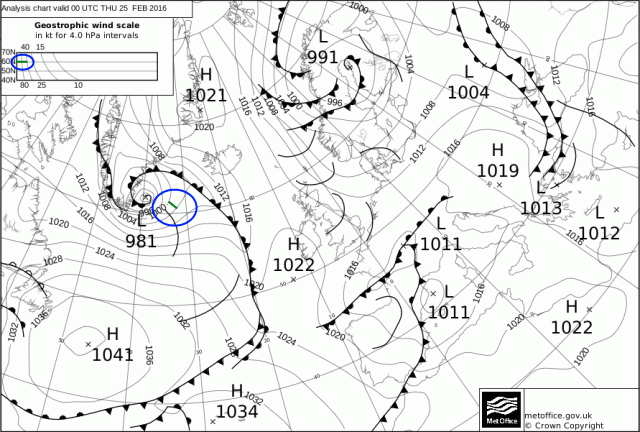
Sur les cartes Isobariques mises à disposition par le service météorologique national du Royaume-Uni (UK Met Office), une petite abaque libellée "Geostrophic wind scale in kt for 4.0 hPa intervals" apparaît dans le coin supérieur gauche de la carte (voir Figure 3 ci-dessus). La Vitesse du vent en altitude dans une région donnée peut alors se déterminer sans calcul comme suit. Sur la carte, il suffit d'interpoler la Latitude de la région entre deux Parallèles proches, puis de reporter horizontalement dans l'abaque, pour cette Latitude donnée, le segment de droite joignant perpendiculairement les deux Isobares encadrant la région. L'extrémité droite de ce segment indique alors, sur la courbe de l'abaque, la Vitesse du vent en noeud marin ou knot (1 kt = 1,852 km/h).
Sur l'exemple de la Figure 3, la région considérée (cerclée d'un trait bleu) se situe à quelques centaines de kilomètres à l'est de la pointe du Groenland, au niveau du 60e Parallèle Nord. Le segment de droite joint les deux Isobares 1000 hPa et 1004 hPa. Reporté dans l'abaque, il donne une vitesse de 40 noeuds pour le Vent en altitude.
Ensuite, pour avoir la Vitesse du vent au sol, il faut tenir compte de l'atténuation du Vent au sol (voir Vent en altitude et vent au sol).
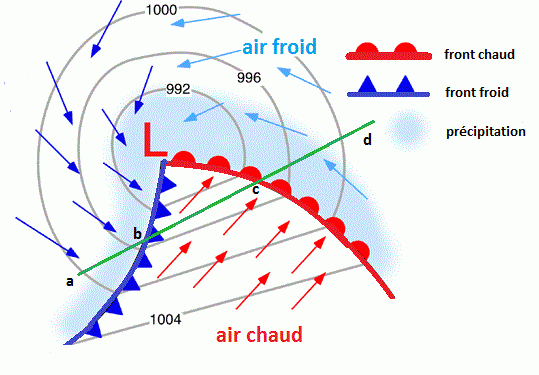
Les Fronts indiqués sur une carte météo de surface sont les lignes d'intersection des surfaces Frontales avec le sol.
Le Front est froid si la masse d'air froid passe sous la masse d'air chaud en la repoussant. Le Front froid se situe à l'arrière de la Dépression et se symbolise généralement par une ligne bleue avec des triangles latéraux qui pointent dans la direction de déplacement du Front (voir Figure 4 ci-dessus).
Le Front est chaud si la masse d'air chaud passe au-dessus de la masse d'air froid en la repoussant. Le Front chaud se situe à l'avant de la Dépression et se symbolise généralement par une ligne rouge avec des demi-cercles latéraux qui pointent dans la direction de déplacement du Front (voir Figure 4 ci-dessus).
Le Front est dit "occlus" lorsque le Front froid rattrape le Front chaud et rejette en altitude l'air chaud coincé entre les deux Fronts. Il se symbolise généralement par une ligne violette avec des triangles et des demi-cercles alternés qui pointent dans la direction de déplacement du Front.
Chaque Front apporte du mauvais temps (voir Evolution des nuages).
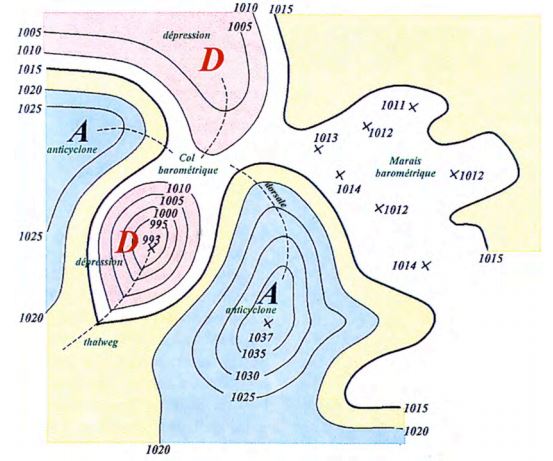
L'identification des dorsales, thalweg, cols et marais barométriques sur une carte de surface Isobarique permet une analyse plus complète d'une situation météorologique sur une grande échelle (voir Figure 5 ci-dessus).
- Dorsale (ou crête barométrique) : excroissance d'un Anticyclone. Zone de beau temps. Derrière une Dorsale arrive souvent une Perturbation (Front chaud).
- Thalweg (ou talweg ou creux barométrique ou vallée) : excroissance d'une Dépression. Zone de mauvais temps. Dans l'axe d'un thalweg se trouve souvent un Front froid (voir Figure 5 ci-dessus), avec brusque rotation du Vent au passage du thalweg (voir Figure 4 ci-dessus).
- Col barométrique (ou selle de cheval) : région située entre deux Anticyclones et deux Dépressions disposés en croix, et généralement située entre deux Dorsales ou deux Thalweg se faisant face. Zone de forte humidité due au manque de ventilation. Propice aux Brouillards en hiver et aux Orages en été.
- Marais barométrique (ou plaine ou plateau) : région étendue à très faible variation de pression (Isobares fortement espacés). Zone de mauvais temps stagnant, avec Vents de Relief (régime de brise). Propice à la formation de Cumulonimbus avec Brouillards et Orages. Le "pot au noir" est un exemple de marais barométrique des zones équatoriales, où la navigation est rendue difficile par la Pluie, les Orages et la faible visibilité.
La biométéorologie est une science qui étudie l'impact des phénomènes atmosphériques sur les êtres vivants (plantes, animaux et humains).
Les variables atmosphériques étudiées sont principalement la température, le rayonnement solaire, le Vent, l'Humidité, la pression, la pollution (naturelle ou humaine) et l'électricité.
Attention : la biométéorologie est une nouvelle branche des sciences météorologiques qui a besoin de faire ses preuves.
Sur l'homme, la biométéorologie concerne quatre classes d'effets physiologiques (cf [CHOISNEL, L'homme, pp 37-38][CHOISNEL, Les enjeux, pp 9-10]) :
1- Les effets thermiques faisant intervenir la vasoconstriction des vaisseaux sanguins et le frissonnement dans la gamme thermique froide, la vasodilatation et la sudation dans la gamme thermique chaude. Les fonctions concernées sont la thermorégulation, la respiration et les processus physiologiques de l'équilibre hydrique du milieu intérieur. Les variables météorologiques pertinentes dans les deux gammes sont la température de l'air, la Vitesse du vent et les rayonnements solaire et infrarouge thermique, ainsi que l'Humidité absolue de l'air dans la gamme chaude.
Deux bilans thermiques sont à distinguer : celui du corps humain pris dans son ensemble et celui des extrémités (visage, nez, mains, doigts, etc.), ces derniers étant particulièrement sensibles au froid et au vent.
2- Les échanges gazeux liés à la composition chimique de l'air inspiré par les voies respiratoires. Ils s'accompagnent d'une déperdition d'eau pour l'organisme. Les fonctions concernées sont la respiration, la circulation et les processus physiologiques de l'équilibre hydrique du milieu intérieur. Les variables météorologiques pertinentes sont les pressions partielles de vapeur d'eau, d'oxygène et de gaz carbonique, ainsi que la détection des Aérosols.
On peut y rajouter la température et l'humidité de l'air inspiré, dont les effets sont l'irritation des bronches pour un air très froid, le dessèchement des muqueuses de l'appareil respiratoire favorisant la secrétion de mucosités pour un air chaud et sec, la dilatation de ces muqueuses avec risque de nez bouché et de gêne respiratoire pour un air très humide.
3- Les effets biochimiques cutanés. Les fonctions concernées sont le système endocrinien, notamment dans le processus de synthèse de la vitamine D. Les variables météorologiques pertinentes sont le rayonnement solaire dans les différentes gammes ultraviolettes (UVC, UVB, UVA).
Les rayons UVC ne parviennent pas au sol grâce à la protection assurée par la couche d'ozone atmosphérique.
Les rayons UVB pénètrent dans l'épiderme et sont filtrés efficacement par la mélanine synthétisée par l'organisme et responsable du bronzage cutané. Les rayons UVB agissent aussi sur le système immunitaire. Ainsi, l'abus de l'exposition au soleil affaiblit la surveillance immunologique des cellules de Langerhans situées dans la couche cornée, favorisant le développement de cancers cutanés.
Les rayons UVA pénétrent jusqu'au derme et sont principalement responsables du vieillissement de la peau.
4- Les effets électriques liés à l'occurence d'orages. Les fonctions concernées seraient la respiration et le système nerveux. Les variables météorologiques pertinentes sont le gradient vertical de potentiel électrique, le comptage des décharges atmosphériques, l'ionisation et la conductibilité électrique de l'air.
Concernant les effets de l'ionisation atmosphérique, peu d'expérimentations indépendantes confirment les résultats obtenus. On peut cependant citer trois effets d'un excès d'ions gazeux chargés positivement : une diminution de la mobilité des cils vibratiles de la trachée-artère, une diminution de la capacité pulmonaire totale et un assèchement de la surface des muqueuses de la trachée.
Au-delà de ces effets physiologiques, plus ou moins ressentis en fonction de sa propre "météosensibilité", on peut rajouter une cinquième classe regroupant les effets psychologiques qui ne sont pas liés directement aux conditions météorologiques mais à leurs conséquences sur les êtres humains en termes de pensées, d'émotions et de comportements.
On peut citer en exemples, en allant du plus confortable au plus inconfortable :
- Par beau temps, on sort plus, on rencontre des amis et le moral n'est que meilleur.
- Par temps de pluie et sans aucun vent, on peut prendre plaisir à sortir (avec un parapluie), car : "enfin, il se passe quelque chose !" ou bien : "enfin seul, loin de la foule déchaînée !".
- Par temps de pluie ou par vent fort, on reste chez soi et l'immobilité accrue peut favoriser les douleurs rhumatismales.
- Par pleine lune avec ciel dégagé, la luminosité est plus importante et on peut avoir du mal à s'endormir.
- Par vent fou (Autan, Sirocco, Foehn...), on peut se sentir énervé ou simplement nerveux, voire indifférent, ou au contraire excité voire euphorique.
- Par brusque changement de temps, on peut se sentir contrarié par les événements, voire dépassé, voire agressé.
- L'idée du changement climatique peut causer chez certains une souffrance psychique : impression de péril imminent, profondes angoisses de fin du monde, impossibilité à se projeter dans l'avenir.
Quant aux animaux, ils ne prévoient pas le temps de demain. Ils réagissent simplement plus vite que nous aux changements de température, d'humidité et de pression qui s'opèrent constamment dans l'atmosphère.
Les Nuages, et le temps en général, font l'objet de nombreux dictons.
Sont listés ci-dessous les principaux dictons ayant une explication scientifique connue (cf [KOHLER]).
Ciel et vent :
- Arc-en-ciel du matin, pluie sans fin,
- Arc-en-ciel du matin, abreuve le moulin,
- Arc-en-ciel du matin, du laboureur finit la journée : un arc-en-ciel vu le matin signifie que le rideau de Pluie se trouve à l'ouest, par où arrivent les Perturbations. La fin de journée, et peut-être les suivantes, est donc placée sous le signe de la Pluie.
- Brouillard à la nouvelle Lune, signe de pluie pour le déclin de la Lune : le brouillard indique une atmosphère saturée en humidité, signe de perturbation à venir si l'air reste humide.
- Rosée du soir, il va pleuvoir : l'air saturé d'humidité, avec une température qui va continuer à baisser, indique une Bruine à venir.
- Herbe sans rosée, signe de pluie : un matin sans rosée peut résulter d'une nuit chaude chargée de vapeur d'eau, signe d'une Perturbation à venir (Orage ou Pluie) dans la journée.
- Le vent la nuit, la pluie avant midi : habituellement, le vent tombe à la tombée de la nuit car les différences de température entre masses d'air proches tendent à s'estomper et, du même coup, l'appel d'air qu'elles créent. Dans la négative, une Perturbation pluvieuse approche donc.
- Vent au visage rend marin sage : sur un voilier, un vent de face ou de côté est idéal pour le marin.
Soleil et Lune :
- Si plus qu'à l'ordinaire les étoiles grossissent, c'est de l'eau que bientôt les nuages vous pissent : le soir, une auréole autour des étoiles, paraissant grossir les plus brillantes, est provoquée par une fine couche nuageuse transparente, signe d'une Perturbation prochaine.
- Lune cerclée, pluie assurée,
- Lune aux cercles pâlots, fait sortir les escargots,
- Cercle à la Lune, matelot dans la hune,
- Cercle à la Lune vers le soir, vent et pluie à minuit : les cercles (halos) entourant la Lune sont dus à la réfraction de la lumière par des cristaux de glace de nuages très fins. Ces nuages élevés (Cirrus) annoncent une Perturbation.
- Ne crois pas de l'hiver avoir atteint la fin, que la Lune d'avril n'ait atteint son plein : allusion à la Lune rousse, pendant laquelle les nuits claires entraînent une perte de chaleur par rayonnement, rendant une gelée possible.
- Lune à cache-cache derrière les nuages, c'est de la pluie ou des orages,
- Lune barbouillée appelle vent et giboulée : les nuages élevés masquant la Lune annoncent une Perturbation.
Nuages :
- Si, par ciel très noir, il ne pleut pas le soir, soyez certain que c'est pour le lendemain : des nuages noirs annoncent Pluie ou Tempête.
- Rouge le matin, trempe le voisin,
- Rouge le matin, pluie en chemin,
- Rouge le matin, chagrin : lorsque le temps est nuageux et que le Soleil est bas sur l'horizon (donc le matin ou le soir), la lumière émise est rougeoyante car les rayons du Soleil sont fortement diffractés à travers les nuages. Aux latitudes moyennes, un ciel rouge au soleil levant (le matin à l'est) indique du mauvais temps, car les Perturbations se déplacent généralement de l'ouest vers l'est et leur tête à l'est le matin annonce le corps pluvieux approchant par l'ouest.
- Ciel pommelé, vent va souffler,
- Ciel moutonné, beau temps pressé,
- Ciel pommelé et femme fardée sont de courte durée,
- Nuages pommelés et femme fardée ne sont pas de longue durée : le ciel pommelé correspond à des nuages de type Cirrocumulus qui précèdent les nuages bas annonciateurs d'une Perturbation.
- Nuages en griffe, pluie prochaine : le ciel en griffe correspond à des nuages de type Cirrus uncinus, signe de Pluie si le nuage grossit.
- Brebis, qui paissent aux cieux, font temps venteux et pluvieux,
- Ciel vêtu de laine, eau peu lointaine : le ciel avec petits moutons correspond à des nuages de type floccus, signe de Pluie.
- Des nuages obscurs, jaunes ou verts, annoncent grêle avec éclairs : ce ciel peut correspondre à des nuages de type Cumulonimbus, signe de grêle et d'Orage.
- Des nuages jaunes ou violets, du vent à tout emporter : ce ciel peut correspondre à des nuages de type Cumulonimbus, signe de rafale violente.
- Si passent nuages bas et unis, la pluie n'attendra pas minuit : ce ciel peut correspondre à des nuages de type Cumulus congestus, signe de Pluie.
Animaux et humains :
- Si l'hirondelle vole bas, viendra la pluie à grand fracas,
- Hirondelle volant bas, bientôt il pleuvra : quand la pression atmosphérique est basse, signe de mauvais temps, les moucherons volent bas car leurs ailes sont alourdies par l'air humide. Les hirondelles, pour s'en nourrir, volent bas elles aussi.
- Oiseaux de mer se réfugiant dans les terres, tempête à venir d'une forte manière : lorsque la pression de l'air baisse en raison d'une Tempête imminente, les oiseaux de mer reviennent rapidement sur la côte pour se protéger.
- Escargot aventureux, le temps sera pluvieux : les escargots adorent l'humidité. Ils sortent leurs antennes à l'approche des nuages.
- Araignée tissant, mauvais temps : l'araignée renforce sa toile lorsque le vent se fait sentir.
- Araignée du matin, chagrin. Araignée du midi, souci. Araignée du soir, espoir : un matin sans rosée permet à l'araignée de tisser sa toile sans gêne mais indique aussi une Pluie prochaine. Dans ce cas, elle doit se dépêcher de tisser sa toile avant midi (au lieu du soir quand tout est calme).
- Si le coq chante le soir, c'est signe qu'il va pleuvoir. S'il chante à midi, signe d'un temps de paradis : un coq qui chante tardivement peut ressentir l'humidité qui précède une perturbation.
- Si les poules restent sous la pluie, celle-ci n'est pas de sitôt finie : une poule qui ne cherche pas à se mettre à l'abri est un signe que la pluie va durer longtemps.
- Vieilles douleurs, pluie de malheur : une forte augmentation de l'humidité de l'air annonce l'arrivée de la Pluie. Cette augmentation, de même qu'elle fait gonfler le bois (tiroirs qui se bloquent, portes qui frottent), agirait sur nos articulations en provoquant des douleurs articulaires plus prononcées. A noter : à ce jour, il n'y a pas de preuves scientifiques de bonne qualité qui permettent de valider ou d'invalider le fait que l'humidité augmente les douleurs rhumatismales (cf [MANSON]).
Ciel et vent :
- Arc-en-ciel du soir met la pluie en retard,
- Arc-en-ciel du soir fait beau temps prévoir : un arc-en-ciel vu le soir signifie que le rideau de Pluie se trouve à l'est, par où arrivent rarement les Perturbations. Il s'agit donc de la fin d'une Perturbation.
- Pluie du matin n'arrête pas le pèlerin,
- Pluie du matin passe son chemin : l'augmentation de température avec la montée du Soleil dans le ciel permet de maintenir les nuages sans provoquer de Pluie.
- Rosée du matin, tout va bien : l'augmentation de température avec la montée du Soleil dans le ciel permet d'absorber le trop-plein d'humidité sous forme de petits Cumulus, signe de beau-temps à venir.
- Brume basse, beau temps amasse,
- Brouillard d'automne, beau temps vous donne,
- Brouillard dans la vallée, pêcheur, fais ta tournée,
- Brouillard dans la vallée, bonhomme, va à ta journée. Brouillard sur le mont, bonhomme, reste à la maison : un Brouillard de vallée (Stratus) est signe de beau temps alors qu'un Brouillard de montagne (Stratus) dénote un air humide et donc du mauvais temps.
- Si le vent saute du sud au nord, plie ta voile et dors : la Perturbation venant du sud s'éloigne.
Soleil et Lune :
- Si le Soleil se fait beau lit le soir, le lendemain beau temps se fait voir : le soir, après un temps pluvieux, des éclaircies indiquent la fin de la Perturbation.
- Si le Soleil plonge dans l'eau à son lever, le soir n'en sera que plus beau : un ciel dégagé le matin est souvent synonyme d'une masse d'air stable, laissant prévoir un temps clément pour plusieurs heures, y compris le soir.
- Lune brillante et blanche, pour plusieurs jours le beau temps,
- Si la Lune brille en clarté, le temps sec est apprêté : une Lune bien visible, avec des bords très nets se découpant dans le ciel, traduit une grande transparence de l'air, donc l'assurance d'un temps sec et d'un beau temps.
Nuages :
- Rouge du soir, bon espoir : lorsque le temps est nuageux et que le Soleil est bas sur l'horizon (donc le matin ou le soir), la lumière émise est rougeoyante car les rayons du Soleil sont fortement diffractés à travers les nuages. Aux latitudes moyennes, un ciel rouge au soleil couchant (le soir à l'ouest) indique du bon temps, car les Perturbations se déplacent généralement de l'ouest vers l'est et leur traîne à l'ouest le soir annonce que le corps pluvieux s'est déjà éloigné vers l'est.
- Rouge vêpre et blanc matin sont la joie et le souhait du pélerin : un ciel rouge au crépuscule ou clair le matin est signe de beau temps à venir.
- Beau temps en vue s'il y a dans le ciel assez de bleu pour tailler une culotte de gendarme : un fond de nuages pluvieux (Nimbostratus) avec déchirures laissant apparaître quelques coins de ciel bleu indique la fin de la Perturbation, signe d'un temps sec et ensoleillé à venir.
Animaux et humains :
- Coccinelle vole haut, il fera beau,
- Hirondelle volant haut, le temps reste au beau : quand la pression atmosphérique est élevée, signe de beau temps, les moucherons volent plus haut afin de se déplacer plus facilement dans un air moins dense. Coccinelles et hirondelles, pour s'en nourrir, doivent voler plus haut elles aussi.
- Moucherons au coucher du Soleil, pour demain temps vermeil,
- Chauve-souris très tard le soir, pour plusieurs jours de beau temps l'espoir : les insectes sont plus actifs quand les conditions atmosphériques sont stables, sans pluie ni vent fort, ce qui est signe de temps calme et ensoleillé.
La navigation aérienne et maritime couvre les principes, les techniques et les pratiques permettant de conduire un mobile (avion ou navire) depuis son lieu de départ jusqu'à sa destination, compte-tenu des conditions météorologiques et des obstacles éventuels. Elle fait appel aux notions de base suivantes :
1- Les projections cartographiques
2- Les distances orthodromique et loxodromique
3- Les routes
4- Les caps
5- Les vitesses vents
6- Les relèvements et gisements
7- Le triangle des vitesses
8- Les allures et le réglage des voiles
9- L'équilibre d'un voilier
La projection cartographique du globe terrestre permet de représenter sa surface non plane sur une carte plane selon une transformation mathématique faisant correspondre les points du globe aux points de la carte.
La représentation sur carte des Méridiens et des Parallèles est appelée canevas.
Trois types principaux de transformation mathématique existent :
- Transformation conforme ou orthomorphique : elle conserve localement les angles, donc les formes, et s'utilisent surtout en topographie et géodésie (exemples : cartes IGN et marines). Les images des Méridiens et des Parallèles se coupent aux bons angles.
- Transformation équivalente : elle conserve localement les surfaces et s'utilisent surtout dans les atlas.
- Transformation équidistante : elle conserve les distances sur les Méridiens et s'utilisaient notamment dans les cartes anciennes (exemple : cartes de Cassini).
Le principe est de faire une projection géométrique sur des surfaces développables (surfaces pouvant être étalées sans déformation sur un plan).
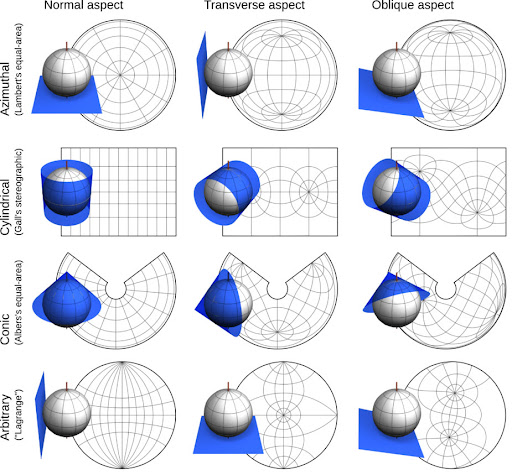
Les trois surfaces développables les plus courantes sont le cône, le cylindre et le plan, lesquels déterminent différents aspects de la projection (voir Figure 1 ci-dessus) : normal, direct ou polaire lorsque l'axe de la surface coïncide avec le rayon polaire du globe, transverse ou équatorial lorsque l'axe de la surface coïncide avec un rayon équatorial du globe, oblique dans les autres cas.
Ces surfaces développables induisent trois types de projection (cf [DUQUENNE, Représentations]) :
- Projection conique : projection des points du globe depuis son centre sur un cône tangent à un cercle du globe ou sécant en deux cercles (voir Figure 1 ci-dessus).
Dans le cas d'une projection d'aspect normal, les Parallèles ont pour image des arcs de cercle concentriques et les Méridiens ont pour image des demi-droites concourantes au centre des arcs de cercle, formant entre elles un angle constant (voir Figure 1 ci-dessus).
On rencontre usuellement les projections coniques de types "conforme de Lambert" et "équivalente d'Albers" (cf [LAPAINE]).
- Projection cylindrique : projection des points du globe depuis son centre sur un cylindre tangent à un grand cercle du globe ou sécant en deux cercles (voir Figure 1 ci-dessus).
Dans le cas d'une projection d'aspect normal, les Parallèles ont pour image des droites parallèles et les Méridiens ont pour image des droites parallèles équidistantes perpendiculaires aux premières (voir Figure 1 ci-dessus).
On rencontre usuellement les projections cylindriques de types "conforme de Mercator" et "équivalente de Lambert" (cf [LAPAINE]), mais aussi de type équidistante (exemple : cartes Google Earth).
- Projection azimutale ou zénithale ou planaire : projection des points du globe depuis un point focal F sur un plan tangent en un point du globe ou sécant en un cercle (voir Figure 1 ci-dessus).
Dans le cas d'une projection d'aspect normal, les Parallèles ont pour image des cercles concentriques et les Méridiens ont pour image des demi-droites concourantes au centre des cercles, formant entre elles un angle constant (voir Figure 1 ci-dessus).
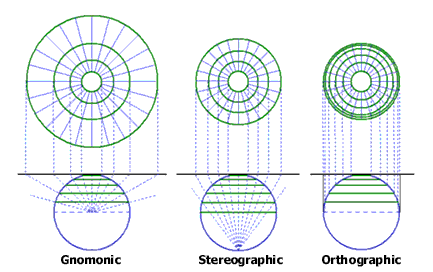
Trois types principaux de projection azimutale existent. La projection est dite gnomonique pour F = centre du globe, stéréographique pour F = point du globe à l'opposé de la carte, et orthographique ou orthogonale pour F = point à une distance infinie de la carte (voir Figure 2 ci-dessus).
On rencontre usuellement les projections azimutales de type "stéréographique" et "équivalente de Lambert", cette dernière étant quasi-stéréographique (cf [LAPAINE]), ainsi que les projections de type orthographique (exemple : cartes en astronomie).
Attention : Une projection cartographique n'est pas toujours une projection purement géométrique. Ainsi, pour la projection cylindrique de Mercator, l'écartement des Parallèles est calculé mathématiquement pour que la carte soit conforme, et donc utilisable en navigation.
En météorologie (cf [CALAS]), l'ellipsoïde terrestre n'est pas considérée et tous les calculs se font sur une sphère selon une projection de type :
- cylindrique normal de Mercator qui est conforme,
- conique normal de Lambert qui est conforme,
- azimutale stéréographique polaire qui est conforme (cas courant des cartes Météo-France),
- ou azimutale orthographique (polaire, équatorial ou oblique) qui n'est jamais conforme ou équivalente.
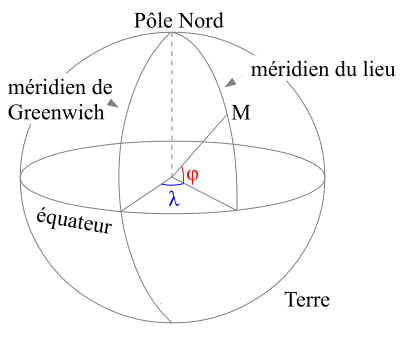
Le globe terrestre se modélise géométriquement par une ellipsoïde de révolution de rayon équatorial a et de rayon polaire b (voir Annexe).
Dans le cas où on assimile le globe terrestre à une sphère parfaite, on en déduit les deux propriétés suivantes :
- Le rayon moyen Rmoyen de la sphère qui se rapproche au mieux de l'ellipsoïde en tout point M vaut Rmoyen = 6371 km (cf [IGN]). Rmoyen est en effet la moyenne arithmétique des trois demi-axes de l'ellipsoïde générale (Rmoyen = (a + a + b)/3).
- la Latitude géographique Φ de l'ellipsoïde équivaut à la Latitude géocentrique φ de la sphère.
Soient deux points quelconques M1 et M2 à la surface terrestre de Latitudes φ1 et φ2, et de Longitudes λ1 et λ2 (voir Figure 1 ci-dessus).
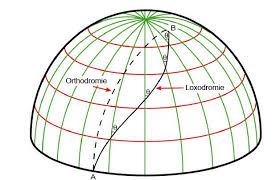
La distance orthodromique entre les deux points M1 et M2 est la route la plus courte autour du globe terrestre entre ces deux points. Sur une sphère, cette route est le plus petit des deux arcs de grand cercle joignant les deux points (voir Figure 2 ci-dessus).
La distance loxodromique est la route suivie par un mobile (avion ou navire) autour du globe terrestre entre ces deux points en suivant un cap constant. Sur une sphère, cette route est une courbe qui coupe les Méridiens et les Parallèles sous un angle constant (voir Figure 2 ci-dessus).
Le gain en distance entre orthodromie et loxodromie n'est vraiment significatif que sur des longs parcours (traversée océanique ou trajet aérien intercontinental) et aux hautes Latitudes.
Sur une sphère, la distance orthodromique do12 entre deux points quelconques M1 et M2 peut se calculer comme suit (cf [IGN]) :
do12 = Rmoyen θ12
θ12 (en radian) = Arccos( sin(φ1) sin(φ2) + cos(φ1) cos(φ2) cos(λ2 - λ1) )
la fonction Arccos() étant comprise entre 0° et 180°
Ainsi, un écart de Latitude |φ2 - φ1| de 1° correspond à do = 111 km, et un écart de Longitude |λ2 - λ1| de 1° à la Latitude de Paris (φ1 = φ2 = 49°) correspond à do = 73 km.
Sur une sphère, la distance loxodromique dl12 entre deux points quelconques M1 et M2 peut se calculer comme suit (cf [Wikipedia, Loxodromie]).
Le calcul exact existe mais est compliqué. Le calcul approché repose sur les formules ci-dessous qui ne s'appliquent que pour des points à distance réduite (inférieure à 300 milles marins) et à des latitudes éloignées des pôles (latitudes inférieures à 60°), la route loxodromique perdant tout intérêt dans ce second cas car devenant une spirale qui s'enroule autour du pôle.
dl12 = Rmoyen Δφ / cos(Rv)
tg(Rv) = P = cos(φmoyen) Δλ / Δφ
Δφ = φ2 - φ1
Δλ = λ2 - λ1
φmoyen = (1/2)(φ1 + φ2)
Rv = Route vraie.
Cette convention de repérage induit les résultats suivants pour Rv en fonction du paramètre P :
Si Δφ > 0 et Δλ ≥ 0 alors : Rv = Arctan[P]
Si Δφ > 0 et Δλ < 0 alors : Rv = 360° + Arctan[P]
Si Δφ < 0 alors : Rv = 180° + Arctan[P]
Si Δφ = 0 et Δλ > 0 alors : Rv = 90°
Si Δφ = 0 et Δλ < 0 alors : Rv = 270°
Si Δφ = 0 et Δλ = 0 alors : Rv = indéfini
la fonction Arctan[] étant comprise entre +90° et -90°
Par ailleurs, pour Δφ proche de 0 (correspondant à une Route vraie proche de 90° ou de 270°), la quantité cos(Rv) est proche de 0 et la distance dl12 doit être adaptée comme suit pour le calcul :
dl12 = Rmoyen cos(φmoy) Δλ / sin(Rv)
Ainsi, en allant de Paris (φ1 = 48° 49' Nord = +48,833° ; λ1 = 2° 19' Est = +2,333°) à Brasilia (φ2 = 10° 58' Sud = -10,983° ; λ2 = 68° 45' Ouest = -68,750°), la distance orthodromique vaut do = 9 586 km alors que la distance loxodromique vaut dl = 10 006 km (avec une Route vraie valant Rv = 228,34°).
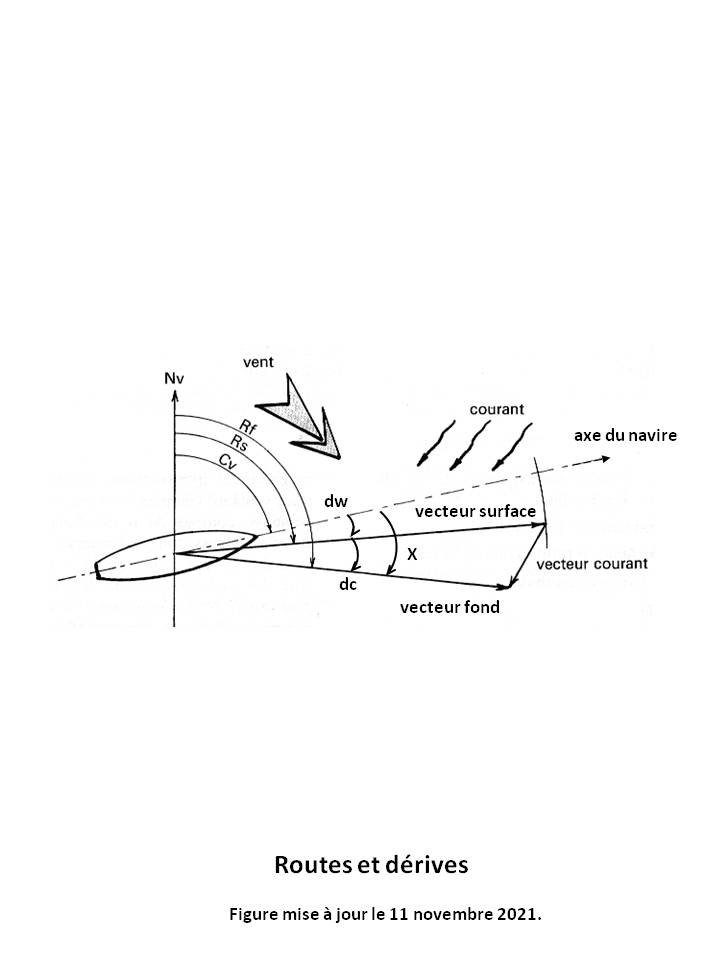
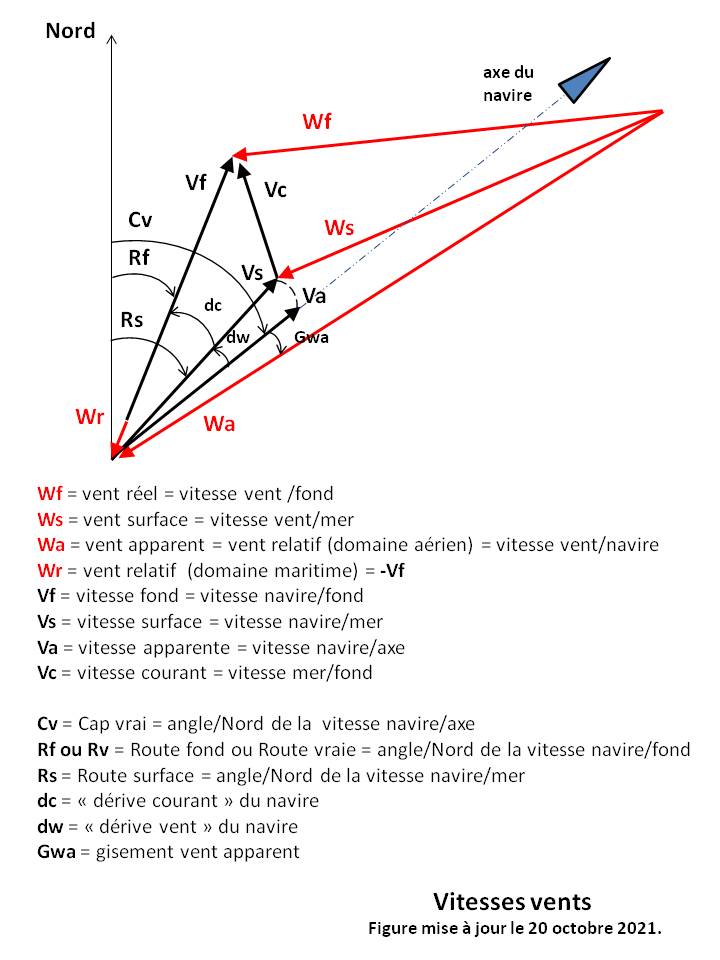
En navigation, la trajectoire d'un mobile (avion ou navire) fait intervenir quatre vecteurs vitesse selon le repère considéré (cf [PARODI]). Voir Figures 1 et 3 ci-dessus.
Vf = vitesse fond = vecteur vitesse du mobile par rapport au fond marin. Il peut se mesurer directement par les GPS.
Vs = vitesse surface = vecteur vitesse du mobile par rapport à la surface de la mer. Son module (Vs = ||Vs||) peut se mesurer par un speedomètre embarqué (intégrant si possible les fortes dérives vent).
Va = vitesse apparente = vecteur vitesse propre du mobile par rapport à sa Ligne de foi et se déduisant de Vs par une rotation d'angle dw.
Vc = vitesse courant = vecteur vitesse du courant marin par rapport au fond. Il se déduit des documents nautiques pour la région et des annuaires des marées.
Attention : La direction du courant marin est celle vers laquelle le courant porte, contrairement à la direction du vent qui est celle d'où vient le vent.
On a la relation vectorielle suivante :
Vf = Vs + Vc
La Route est l'angle du vecteur vitesse du mobile par rapport à la direction du Nord vrai (Nv), mesuré en degrés et dans le sens horaire (de 0° à 360°).
Trois routes sont à distinguer selon le repère considéré (cf [Wikipedia, route (navigation)][PARODI]). Voir Figure 1 ci-dessus.
- La Route vraie (Rv), ou Route sur carte, ou Route fond (Rf) dans le domaine maritime, qui est la Route par rapport au fond marin. Le navigateur fait régulièrement le point par rapport à la route et corrige son cap pour se maintenir sur celle-ci.
- La Route surface (Rs), qui est la Route par rapport à la surface de la mer, donc indépendamment du courant marin. Elle se matérialise par le sillage du mobile à la surface de l'eau.
- Le Cap vrai (Cv), qui est la Route propre du mobile par rapport à sa Ligne de foi, donc indépendamment du vent et du courant marin.
On a les relations suivantes :
Rv = Rf = Rs + dc
Rs = Cv + dw
X = Rv - Cv = dc + dw
dc, dw et X sont respectivement la dérive courant (dc), la dérive vent (dw) et la dérive totale (X), toutes mesurées en degrés et dans le sens horaire. Voir Figure 1 ci-dessus.
dc est la "dérive courant" subie par le mobile et due au courant marin. C'est l'angle du vecteur Vitesse fond Vf par rapport au vecteur Vitesse surface Vs, mesuré en degrés et dans le sens horaire. Le courant peut avoir plusieurs origines : les courants océaniques, la marée, et le vent dans une moindre mesure.
La dérive courant se trace graphiquement connaissant deux vecteurs vitesse : le vecteur Vitesse surface Vs ou le vecteur Vitesse fond Vf du mobile, et le vecteur Vitesse courant Vc du courant marin (voir Le triangle des vitesses).
Attention : : Ne pas confondre "dérive courant" dc (relative au mobile et comptée à partir de son vecteur vitesse) et "Azimut courant" Zc (relatif au courant marin et compté en général à partir de la direction du Nord). Par exemple (voir Le triangle des vitesses), pour une vitesse surface Vs = (10 noeuds, 30°) et une vitesse courant Vc = (5 noeuds, 70°), le navire aura une vitesse fond Vf = (14 noeuds, 43°) et sa dérive courant sera dc = 43° - 30° = 13°. Pour le même "Azimut courant" (Zc = 70°), si la vitesse surface du navire change de direction et devient Vs = (10 noeuds, 70°), alors sa vitesse fond deviendra Vf = (15 noeuds, 70°) et sa dérive courant dc = 70° - 70° = 0°.
dw (noté parfois d) est la "dérive vent" ou plus simplement "dérive", subie par le mobile et due au vent. C'est l'angle du vecteur Vitesse surface Vs par rapport au vecteur Vitesse apparente Va, mesuré en degrés et dans le sens horaire (autrement dit : positivement si le mobile dérive sur sa droite et négativement dans le cas contraire). Cette dérive propre à chaque mobile est un "mal nécessaire" dû à l'action du vent sur toutes les structures découvertes du mobile (sur un navire, toutes les parties émergées). Sur un voilier, elle est maximale quand le mobile navigue au près. Sur un monocoque, la gîte est un bon indicateur de la dérive vent.
En mer, la dérive peut s'estimer en regardant l'angle qui existe entre la Ligne de foi du navire et son sillage. Elle quasiment nulle au portant et peut atteindre 20° au près par vent fort. Sans dérive, le sillage est dans l'axe du navire.
Attention : Ne pas confondre la dérive vent avec la déviation magnétique du compas, toutes deux pouvant s'écrire avec le sigle d.
X (noté parfois der) est la dérive totale subie par le mobile. C'est l'angle du vecteur Vitesse fond Vf par rapport au vecteur Vitesse apparente Va, mesuré en degrés et dans le sens horaire.
A noter que la route est égale au cap en l'absence de dérive.
En navigation, le Cap est l'angle de la Ligne de foi du mobile par rapport à la direction du Nord, mesuré en degrés dans le sens horaire (de 0° à 360°).
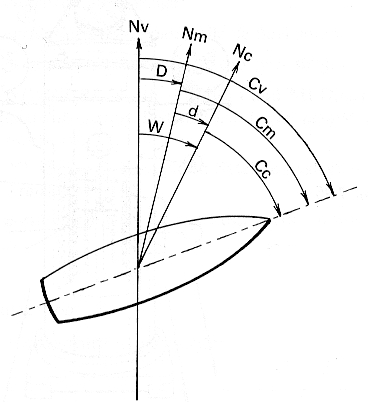
Trois caps sont à distinguer (cf [Wikipedia, cap (navigation)][PARODI]). Voir Figure 2 ci-dessus.
- Le Cap vrai (Cv), qui est le Cap par rapport au Nord vrai (Nv), mesurable directement par un compas satellitaire (sans nul besoin de correction) ou par un compas gyroscopique après correction de la variation gyroscopique.
- Le Cap magnétique (Cm), ou Route magnétique (Rm) dans le domaine aérien, qui est le Cap par rapport au Nord magnétique (Nm), mesurable par un compas magnétique après correction de le déviation magnétique.
- Le Cap compas (Cc), qui est le Cap par rapport au Nord du compas (Nc). C'est le cap que le pilote s'efforce de maintenir pour suivre sa route.
On a les relations suivantes :
Cv = Cm + D
Cm = Cc + d pour un compas magnétique
W = Cv - Cc
W = D + d pour un compas magnétique
W = Wg pour un compas gyroscopique
D, d, W et Wg sont respectivement la Déclinaison magnétique (D), la déviation magnétique (d), la variation compas (W) et la variation gyroscopique (Wg), toutes mesurées en degrés et dans le sens horaire (autrement dit : négativement vers l'ouest et positivement vers l'est). Voir Figure 2 ci-dessus.
Attention aux faux-amis : "Déclinaison (D)" se dit "Variation (V)" en anglais, "déviation (d)" se dit "Compass Deviation (D ou CD)" et "Variation (W)" se dit "Compass Error (CE)".
La déclinaison magnétique D (parfois noté Dm) est l'angle de la direction du Nord magnétique par rapport à la direction du Nord vrai, mesuré en degrés et dans le sens horaire. Il est fonction du lieu considéré et du temps (avec une variation annuelle moyenne de 6' Est en France métropolitaine). En 2021, D vaut 1° Est à Paris et 9° Ouest à Brasilia (cf [NOAA, Calculateurs]). Sur les cartes de navigation, D est indiqué en plusieurs endroits de la carte, dans un schéma en forme de rose de compas.
La déviation magnétique d est l'angle de la direction du Nord compas (pour un compas magnétique censé donner le Nord magnétique) par rapport à la direction du Nord magnétique, mesuré en degrés et dans le sens horaire. Elle est causé par l'environnement métallique et électrique du mobile. Les fers durs de cet environnement agissent comme des aimants permanents, les fers doux comme des aimants passagers induits par le magnétisme terrestre et par les fers durs. Cette déviation, propre au mobile et au compas magnétique embarqué, est donnée par une courbe de déviation fonction du Cap compas (Cc). La courbe approchée théorique, donnée par le mathématicien britannique Archibald Smith (1813-1872), est de la forme : d = d1 + d2 cos(Cc) + d3 sin(Cc) + d4 cos(2 Cc) + d5 sin(2 Cc).
En pratique, sur un navire en bois ou en plastique, on néglige la déviation. Attention : elle peut atteindre 20° si on est proche d'un haut-parleur et 50° sur un navire en acier ou en ferro-ciment (cf [Le Diouris]).
Attention : Ne pas confondre la déviation magnétique avec la dérive vent, toutes deux pouvant s'écrire avec le sigle d.
La variation compas W est l'angle de la direction du Nord compas (pour un compas quelconque, magnétique ou gyroscopique) par rapport à la direction du Nord vrai, mesuré en degrés et dans le sens horaire. Pour un compas satellitaire, cette variation est négligeable (elle ne dépasse pas 0,2° en général).
Attention : Ne pas confondre la variation compas W avec la vitesse du vent W ou avec le W anglais pouvant signifier Ouest.
La variation gyroscopique Wg (ou variation gyro) est l'angle de la direction du Nord compas (pour un compas gyroscopique censé donner le Nord vrai) par rapport à la direction du Nord vrai, mesuré en degrés et dans le sens horaire. La variation Wg nest pas magnétique mais mécanique liée à la rotation de la Terre et aux changements de vitesse du mobile. Elle ne dépasse pas 1° en général.
Le cap à suivre est le Cap compas (Cc) tenu par le pilote (aviation), le timonier (marine marchande ou de guerre) ou le barreur (plaisance).
Pour déterminer le cap à suivre, le navigateur réalise les étapes suivantes :
1- Tracer la Route vraie (Rv) sur la carte, qui peut être calculée facilement si la route est loxodromique (voir Distances orthodromique et loxodromique).
2- Déterminer la Route surface en prenant en compte l'effet du courant (Rs = Rv - dc).
3- Déterminer le Cap vrai en prenant en compte l'effet du vent (Cv = Rs - dw).
4- Corriger le Cap vrai pour tenir compte de la Variation compas et obtenir le Cap compas (Cc = Cv - W).
Exemple numérique :
Un navire suit une route fond (Rf) au 231°.
La déviation compas est de 3° Est (soit d = +3°).
La déclinaison magnétique est de 5° Ouest (soit D = -5°).
Il reçoit le vent sur tribord qui le fait dériver de 10° (soit dw = -10°).
Calculer la route surface (Rs) et le cap compas (Cc) du navire dans les deux cas suivants : 1. Dérive courant négligeable (dc = 0°) ou 2. Vecteur courant Vc de vitesse Vc non négligeable et d'Azimut Vrai Zc.
Solution :
Cas 1 : On a la relation évidente : Rs = Rf - dc = 231°. On applique ensuite la formule : Cc = Cv - (D + d) = Rs - (d + D + dw) = 231° - ((+3°) + (-5°) + (-10°)) = 243°
Cas 2 : On a la relation vectorielle : Vs = Vf + -Vc avec Vc = (Vc, Zc), laquelle donne Rs graphiquement ou par calcul numérique connaissant V1 = (Vf, Rf) et V2 = (Vc, Zc + 180°). Voir Triangle des vitesses. On applique ensuite la même formule : Cc = Rs - (d + D + dw).
C'est le problème inverse du cas précédent. Pour déterminer le route suivie, le navigateur réalise les étapes suivantes :
1- Déterminer le Cap compas.
2- Corriger le Cap compas pour tenir compte de la Variation compas et obtenir le Cap vrai (Cv = Cc + W).
3- Déterminer la Route surface en prenant en compte l'effet du vent (Rs = Cv + dw).
4- Déterminer la Route vraie en prenant en compte l'effet du courant (Rv = Rs + dc).
Exemple numérique :
Un navire suit un cap compas (Cc) au 243°.
La déviation compas est de 3° Est (soit d = +3°).
La déclinaison magnétique est de 5° Ouest (soit D = -5°).
Il reçoit le vent sur tribord qui le fait dériver de 10° (soit dw = -10°).
Calculer la route surface (Rs) du navire.
Calculer ensuite la route fond (Rf) du navire dans les deux cas suivants : 1. Dérive courant négligeable (dc = 0°) ou 2. Vecteur courant Vc de vitesse Vc et d'Azimut Vrai Zc.
Solution :
On applique d'abord la formule : Rs = Cv + dw = Cc + (d + D + dw) = 243° + ((+3°) + (-5°) + (-10°)) = 231°
Cas 1 : On a la relation évidente : Rf = Rs + dc = 231°.
Cas 2 : On a la relation vectorielle : Vf = Vs + Vc avec Vc = (Vc, Zc), laquelle donne Rf graphiquement ou par calcul numérique connaissant V1 = (Vs, Rs) et V2 = (Vc, Zc). Voir Triangle des vitesses.
En navigation aérienne et maritime, trois vecteurs "vitesses vents" sont à distinguer (cf [PARODI]). Voir Figure 3 ci-dessus.
- La vitesse vent fond Wf ou vitesse vent réel, qui est le vecteur vitesse du vent par rapport au sol donc aussi par rapport au fond marin. C'est le vent donné par la météo, celui que pourrait mesurer un gardien de phare.
- La vitesse vent surface Ws, qui est le vecteur vitesse du vent par rapport à la surface de la mer. En mer, c'est le vent dont il faut tenir compte pour calculer ses virements de bord.
- La vitesse vent apparent Wa, qui est le vecteur vitesse du vent par rapport au mobile. En mer, c'est le vent donné par la girouette-anémomètre ou le drapeau sur le navire. Il permet de régler la voilure.
|
Attention : Le "vent vitesse" ou "vent relatif" qui est souvent utilisé a deux définitions différentes (cf [Wikipedia, Vent apparent]) : - Dans le domaine aérien, c'est la vitesse du Vent apparent Wa. - Dans le domaine maritime, c'est la vitesse Wr du vent généré par le déplacement du navire sur le fond, c'est-à-dire l'opposé de la Vitesse fond Vf et l'on retrouve la relation connue : Wa = Wf + Wr correspondant à la phrase : "vent apparent = vent réel + vent vitesse". |
On a les relations vectorielles suivantes (voir Figure 3 ci-dessus) :
Wf = Ws + Vc
Ws = Wa + Vs
Wf = Wa + Vf
Wr = -Vf
Sont définis également deux vecteurs "vitesses vent vrai" (cf [PARODI]) :
Wt = Wa + Va, appelé "vent surface" par ScanNav et ne coïncidant avec la vitesse vent surface Ws que si la dérive vent (dw) était nulle. Rappel : Le vecteur Va se déduit de Vs par une rotation d'angle (dw).
Wv = Wa + (Vf/Vs) Va, appelé "vent vrai" ou "vent réel" par ScanNav et ne coïncidant avec la vitesse vent fond Wf que si la dérive vent (dw) et la dérive courant (dc) étaient nulles. Le vecteur (Vf/Vs) Va se déduit de Vf par une rotation d'angle (dw + dc).
Est défini également le Gisement vent apparent Gwa (cf [PARODI]) qui est l'angle de la direction -Wa (direction d'où provient le vent apparent) par rapport à la Ligne de foi du navire, mesuré dans le sens horaire. Cet angle correspond à l'Allure du bateau.
On a les relations suivantes :
Gwa = Zwa - Cv
Zwa = Azimut Vrai du vecteur -Wa
Attention : La terminologie des vitesses vents n'étant pas universelle, il faut être très prudent dans la lecture des termes contenant le mot "vent".
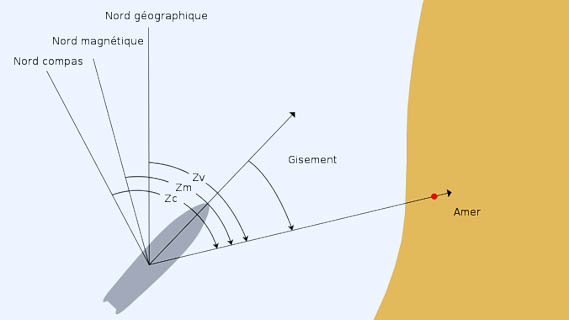
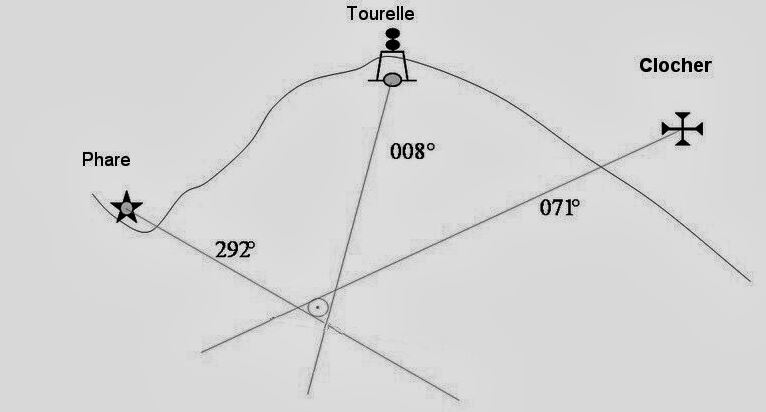
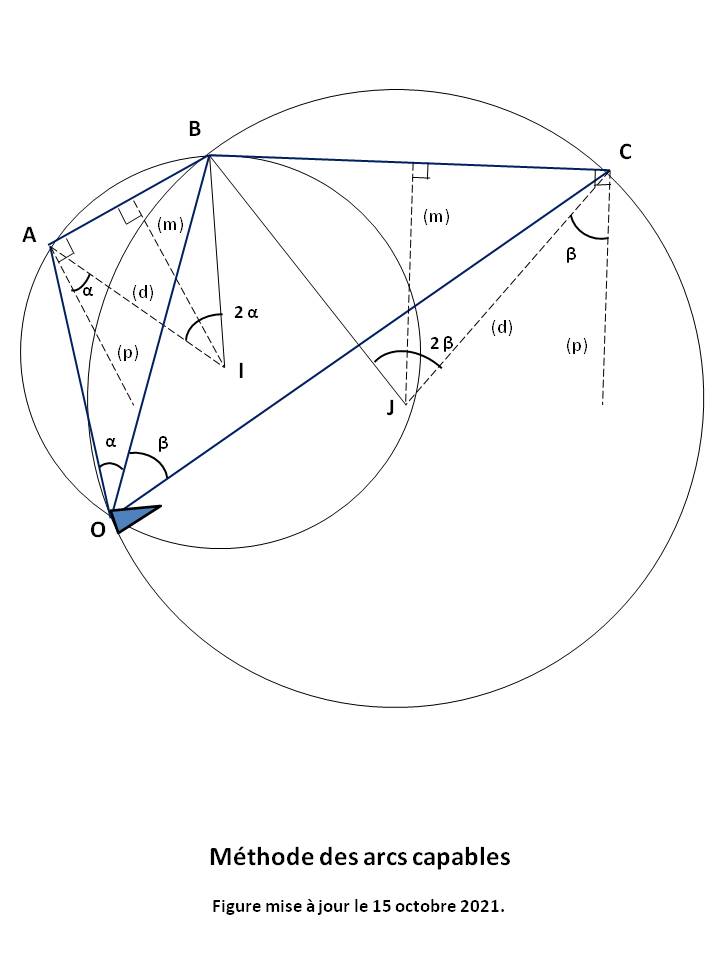
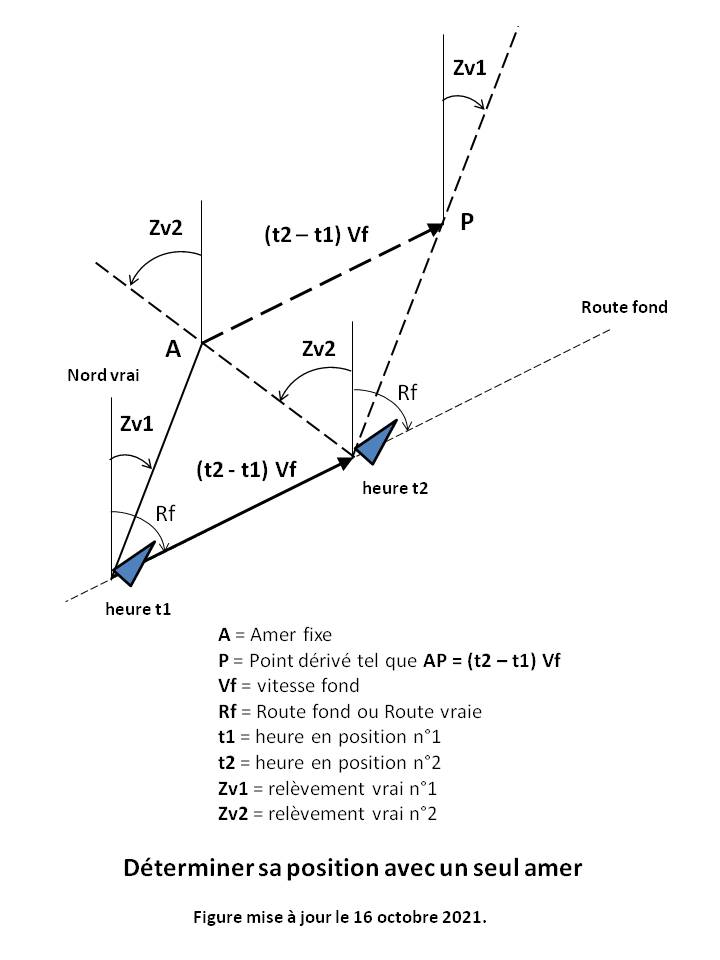
En navigation aérienne et maritime :
- Le relèvement ou azimut (Z) est l'angle horizontal de la direction d'un Amer par rapport à la direction du Nord, mesuré en degrés et dans le sens horaire (de 0° à 360°). Voir Figure 1 ci-dessus. Comme pour les Caps, selon le Nord considéré, trois relèvements sont possibles : relèvement vrai (Zv), relèvement magnétique (Zm) et relèvement compas (Zc). Ce dernier se mesure avec un compas de relèvement.
- Le gisement (G) est l'angle horizontal de la direction d'un Amer par rapport à la direction de la Ligne de foi du mobile, mesuré dans le sens horaire (de 0° à 360°, ou parfois de 0 à 12 "heures" dans le domaine aérien, 9 "heures" indiquant le gisement 270° ou -90°). Voir Figure 1 ci-dessus. Le gisement G se mesure avec un taximètre dont le zéro coïncide avec la Ligne de foi du mobile.
On a les relations suivantes :
Zv = Cv + G
Zm = Cm + G = Zv - D
Zc = Cc + G = Zv - W
La dernière relation montre que pour passer du Relèvement compas Zc (celui effectué au compas de relèvement) au Relèvement vrai Zv (celui lu ou tracé sur la carte), il faut lui ajouter la Variation compas W.
En navigation côtière, pour déterminer sa position sur une carte (c'est-à-dire "faire le point"), le navigateur dispose de plusieurs méthodes, dont les suivantes :
Avec trois Amers écartés l'un de l'autre par rapport à l'observateur, la méthode est la suivante (voir Figure 2 ci-dessus) :
1- Choisir trois Amers écartés l'un de l'autre, idéalement d'un angle horizontal d'au moins 60° entre deux Amers.
2- Pour chaque Amer, lire l'angle Zc donné par le compas de relèvement.
3- Pour chaque Amer, corriger Zc en y ajoutant la Variation compas (Zv = Zc + W) et porter le relèvement corrigé Zv sur la carte en traçant une droite qui passe par l'Amer et qui respecte l'angle Zv avec le Nord vrai.
4- Les trois tracés forment alors un triangle (appelé "chapeau") dans lequel se trouve le navire au moment des relèvements.
Avec trois Amers relativement alignés sur la carte, la méthode (appelée "méthode des arcs capables") est précise et sans nul besoin de la correction W. La méthode est la suivante (voir Figure 3 ci-dessus) :
1- Choisir trois Amers A, B et C relativement alignés sur la carte (afin d'éviter que le cercle passant par A, B et C ne passe aussi par l'observateur O).
2- Mesurer précisément les deux angles horizontaux α = AOB et β = BOC (par exemple, avec un sextant tenu horizontalement, lequel permet de mesurer des angles jusqu'à 120°).
3- Pour les Amers A et B, réaliser les étapes suivantes :
3.1- Tracer la médiatrice (m) du segment AB.
3.2- Tracer de A la perpendiculaire (p) au segment AB.
3.3- Tracer de A la droite (d) faisant un angle α avec (p) du côté de (m).
3.4- Tracer le point d'intersection I de la médiatrice (m) et de la droite (d).
3.5- Tracer le cercle de centre I passant par les points A et B.
4- Pour les Amers C et B, réaliser les traçages comme pour l'étape 3, le cercle de centre J passant par les points C et B.
5- L'intersection des deux cercles donne alors l'emplacement O de l'observateur.
Variante : Les centres I et J des deux cercles peuvent se tracer directement depuis les Amers, après calcul du rayon R de chaque cercle. Pour le segment AB par exemple, on a : R = AI = BI = (1/2) AB / sin(α).
Attention : La méthode n'est pas applicable lorsque l'observateur O se trouve sur le cercle passant par les trois Amers A, B et C.
Explication de la construction (théorème de l'angle capable) : L'ensemble des points P du plan horizontal d'où l'on voit le segment AB sous le même angle α est le cercle passant par les points A, B et P, et l'angle au centre AIB vaut 2 α. Idem pour le segment CB.
Avec deux Amers, la méthode est identique à celle des trois Amers écartés l'un de l'autre, mais moins précise. Les deux tracés donnent, à leur intersection, l'emplacement du navire au moment des relèvements.
Avec un seul Amer, la méthode (appelée "transport d'un lieu" ou "transfert d'Amer") est la suivante (voir Figure 4 ci-dessus) :
1- Pour deux positions successives du navire, noter l'heure (t) et lire l'angle Zc donné par le compas de relèvement en visant l'Amer.
2- Déterminer le vecteur Vitesse fond du navire (Vf) le plus précisément possible (par exemple par GPS).
3- Tracer sur la carte le vecteur (t2 - t1) Vf depuis l'Amer. On obtient ainsi l'emplacement (appelé "point dérivé") qu'aurait l'Amer s'il avait bougé comme le navire.
4- Porter sur la carte le premier relèvement corrigé (Zv1 = Zc1 + D + d) en traçant une droite qui passe par le point dérivé et qui respecte l'angle Zv1 avec le Nord vrai.
5- Porter sur la carte le second relèvement corrigé (Zv2 = Zc2 + D + d) en traçant une droite qui passe par l'Amer et qui respecte l'angle Zv2 avec le Nord vrai.
6- L'intersection des deux droites tracées donne l'emplacement du navire au moment du second relèvement.
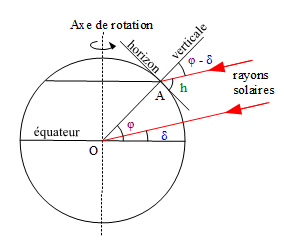
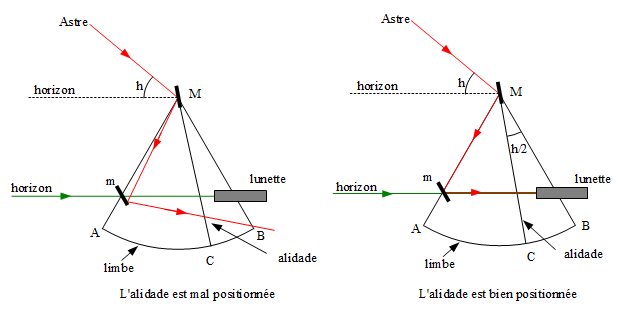
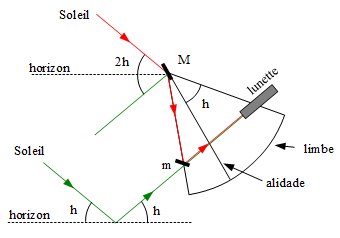
En navigation hauturière, c'est-à-dire au large (sans côtes visibles), d'autres méthodes existent pour faire le point : navigation astronomique et navigation radioélectrique (dont la navigation satellitaire).
Navigation astronomique - Détermination de la longitude : (cf [Navastro, La Méridienne])
La Longitude géographique (λ) d'un lieu d'observation A est l'angle entre le plan passant par le Méridien du point A et le plan passant par le Méridien de Greenwich.
Le Soleil se déplaçant de 15° par heure, la longitude vaut simplement : λ = 15 (HG - H)
avec :
HG = heure TU de passage du Soleil lorsqu'il culmine au méridien de Greenwich (voir Relativité - Lexique - Temps standard). Les Ephémérides donnent cette heure en fonction de la date de l'année (notamment sur le site de Peter Hayes (cf [HAYES]) en sélectionnant : Lieu d'observation = GB : Greenwich ; Date d'observation (exemple) = 2008:02:12 ; Temps civil (résultat pressenti) = 12:14:15 ; Heure solaire (affichée) = 12:00:00).
H = heure TU de passage du Soleil lorsqu'il culmine au méridien du lieu d'observation A (midi solaire local).
Pour avoir une mesure précise de l'heure H, avec un sextant, il faut viser le Soleil avant et après sa culmination pour une même hauteur mesurée. On dispose ainsi de paires d'heures correspondant aux passages successifs du Soleil aux mêmes hauteurs. H est alors la moyenne de ces paires d'heures, et sans besoin de corriger les hauteurs mesurées au sextant.
Exemple :
- Le 12 février 2008, l'observateur mesure la hauteur du Soleil à une hauteur H1 à 12h 50min 46s TU, puis à une hauteur H2 à 12h 58min 49s TU. Après la culmination, l'observateur mesure de nouveau le Soleil à la hauteur H2 à 13h 57min 25s TU, puis à la hauteur H1 à 14h 5min 28s TU.
- L'heure H de la culmination est la moyenne de toutes ces heures, soit : H = (12h 50min 46s + 12h 58min 49s + 13h 57min 25s + 14h 5min 28s) / 4 = 13h 28min 7s TU.
- A cette même date, les Ephémérides montrent que le passage au méridien de Greenwich du soleil s'est fait à HG = 12h 14min 15s TU.
- La longitude cherchée est donc : λ = 15 (HG - H) = 15 (12h 14min 15s - 13h 28min 7s) = -15 (1h 13min 52s) = 18° 28' O
Navigation astronomique - Détermination de la latitude : (cf [DEPARIS, Détermination])
La Latitude géocentrique (φ) d'un lieu d'observation A est l'angle entre la verticale du lieu et le Plan équatorial (voir Figure 1 ci-dessus).
Elle vaut : φ = δ ± (90° - h)
avec :
δ = déclinaison du Soleil = angle entre la direction du Soleil et le Plan équatorial. Les Ephémérides donnent cet angle en fonction de la date et de l'heure dans l'année (notamment sur le site de l'IMCCE (cf [IMCCE])).
h = hauteur du Soleil = angle entre la direction du Soleil et le plan horizontal du lieu d'observation. L'angle vaut 0° lorsque le Soleil est à l'horizon et 90° lorsqu'il passe au zénith du lieu.
la quantité (90° - h) étant affectée du signe + pour le Soleil vu au Sud et du signe - pour le Soleil vu au Nord.
La hauteur h peut se mesurer avec un sextant par exemple (voir ci-après) à condition d'appliquer les corrections suivantes (cf [Wikipedia, Sextant][DESCAMPS, Ephémérides]) : h = hmesurée - d - r + P ± Δ
avec :
hmesurée = hauteur mesurée. Un sextant bien réglé permet une précision de 0,2' d'arc, soit une précision théorique en position de 0,2 milles marins (370 m). En pratique, compte-tenu des mouvements du navire, de la netteté de l'horizon et de l'imprécision de l'heure, les marins obtiennent une précision de l'ordre de 2 milles marins (3,7 km).
d = dépression de l'horizon, fonction de l'altitude z de l'oeil de l'observateur par rapport au niveau de la mer. On a approximativement : d = Arctg[(2 z / Rmoyen)1/2] = 2' (z en mètre)1/2, avec Rmoyen = rayon moyen de la Terre = 6371 km.
r = réfraction atmosphérique qui relèvent les astres, lesquels sont vus toujours plus haut qu'ils ne sont en réalité. On a : r = 0° au zénith, environ 1' à 45° et r maximale à l'horizon. On a approximativement : r = 1' / tg[hmesurée] lorsque hmesurée > 10°
P = parallaxe due au fait que l'observateur est supposé être au centre de la terre. On a : P = 0° au zénith et P maximale à l'horizon. On a approximativement : P = P maximale cos[hmesurée]. P est négligeable pour tous les astres, sauf pour la Lune pour laquelle P maximale = 1° environ.
Δ = demi-diamètre apparent de l'astre, affecté du signe + si on a visé le bord inférieur et du signe - si on a visé le bord supérieur.
Pour le Soleil, les Ephémérides donnent la valeur journalière de Δ ainsi que la quantité Q = - d - r + P + Δm
avec : Δm = demi-diamètre moyen (négligeable pour tous les astres, sauf pour le Soleil et la Lune pour lesquels Δm = 16' environ).
Finalement, la formule à appliquer est : h = hmesurée + Q - Δm ± Δ
Exemple (cf [Navastro, La Méridienne]) :
- Le 12 février 2008, à environ 13h 30min TU, en visant le bord inférieur du Soleil, l'observateur mesure sa culmination à une hauteur hmesurée de 34°53' vers le Sud.
- L'oeil de l'observateur est à une altitude z de 2 m par-rapport au niveau de la mer, d'où : d = 2' (z en mètre)1/2 = 2,8'
- Vu que hmesurée > 10°, la réfraction atmosphérique r vaut approximativement : r = 1' / tg[hmesurée] = 1,5'
- Pour le Soleil, le Parallaxe P est négligeable.
- Le demi-diamètre apparent Δ du Soleil vaut approximativement : Δ = 16'
- La hauteur h après corrections vaut donc, en visant le Soleil sur son bord inférieur : h = hmesurée - d - r + P ± Δ = 34°53' - 2,8' - 1,5' + 0 + 16' = 35° 5'
- A cette même date, les Ephémérides montrent que la déclinaison du Soleil vaut δ = 13° 49' S = -13° 49'
- La latitude cherchée, pour un Soleil vu au Sud, est donc : φ = δ ± (90° - h) = -13° 49' + (90° - 35° 5') = +41° 6' = 41° 6' N
Comment mesurer la hauteur h du Soleil avec un sextant ? (cf [DEPARIS, Détermination]) :
Un sextant est composé principalement d'un bâti portant un limbe gradué en degrés, d'une lunette, de deux miroirs (M et m) et d'une alidade pivotante portant le grand miroir M (voir Figure 2 ci-dessus).
Lorsque les rayons lumineux provenant de l'astre et de l'horizon coïncident, la hauteur h de l'astre visé se lit directement sur le limbe correspondant à un pivotement de l'alidade d'un angle égal à h/2 (voir Figure 3 ci-dessus).
En mer, plutôt que de faire coïncider le centre du Soleil avec l'horizon, il est plus facile de faire tangenter sur l'horizon le bord inférieur du Soleil. La mesure doit alors être corrigée d'environ +16' correspondant au demi-diamètre du Soleil.
Sur terre, lorsque qu'on ne peut pas viser la surface de la mer pour avoir l'horizon, l'astuce consiste à viser le reflet du Soleil sur la surface d'un étang ou d'un simple bac rempli d'eau (voir Figure 4 ci-dessus). La mesure est effectuée lorsque les deux images du Soleil coïncident parfaitement. L'angle mesuré est alors égal au double de la hauteur h du soleil.
Pour avoir une mesure précise, il faut viser le Soleil lorsqu'il culmine au méridien (midi solaire local), ce qui présente deux avantages : 1) on n'a pas besoin de connaître l'heure exacte de passage au méridien ; 2) on a le temps d'effectuer plusieurs mesures et de comparer les résultats.
Attention : Avant de se lancer dans les mesures, il convient de contrôler l'étalonnage du sextant. Il suffit de viser une étoile bien brillante en plaçant l'alidade à la graduation 0°. L'image directe et l'image réfléchie de l'étoile doivent être confondues.
En navigation aérienne, pour déterminer sa position sur une carte, le navigateur dispose de plusieurs méthodes, dont les suivantes :
- Radionavigation à base terrestre : par radiobalises fixes situées au sol (gonio VDF, radiocompas ADF/NDB, radiophare VOR, transpondeur DME, systèmes LORAN-C, DECCA et OMEGA, etc.). La plupart de ces systèmes sont devenus obsolètes depuis l'arrivée du GPS.
- Radionavigation satellitaire : par constellation de satellites en orbite terrestre (voir Relativité - Lexique - GPS).
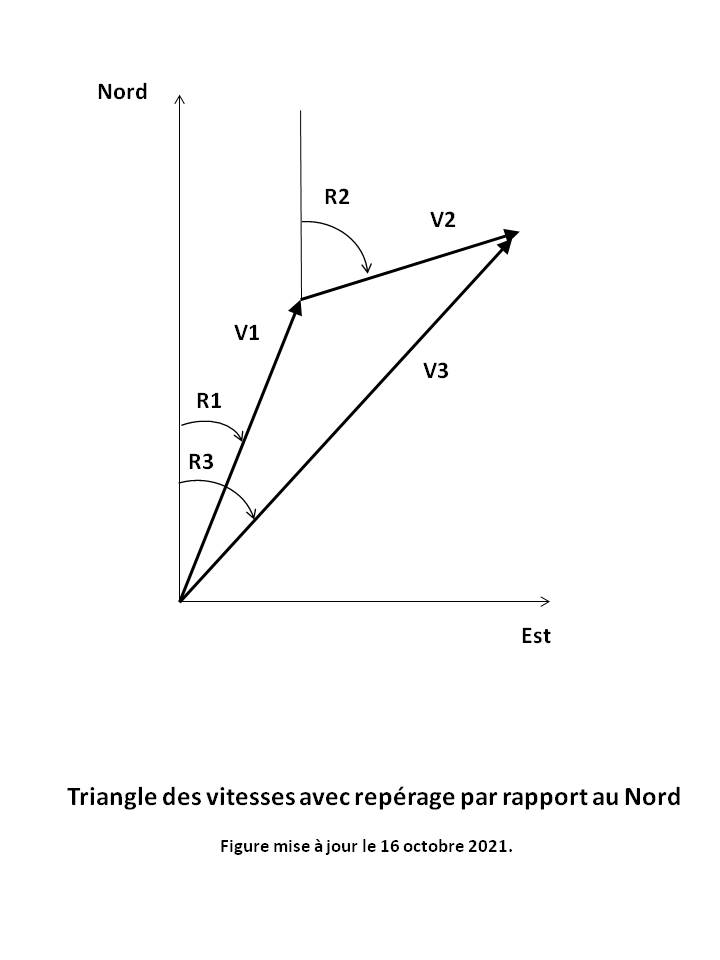
En navigation aérienne et maritime, il est parfois utile de pouvoir calculer informatiquement la somme V3 de deux vecteurs vitesses quelconques V1 et V2 lorsqu'ils sont tous repérés par rapport au Nord.
Par exemple :
- Dans le domaine maritime, on peut vouloir calculer la vitesse V3 du navire par rapport au fond marin connaissant la vitesse V1 du navire par rapport à la surface de la mer et la vitesse V2 du courant par rapport au fond, tel que : V3 = V1 + V2.
- Dans le domaine aérien, on peut vouloir calculer la vitesse V3 de l'avion par rapport au sol connaissant la vitesse V1 de l'avion par rapport au vent et la vitesse V2 du vent par rapport au sol, tel que : V3 = V1 + V2.
- Inversement, on peut vouloir calculer V1 tel que : V1 = V3 - V2, auquel cas on se ramène au calcul d'une somme : V1 = V3 + (-V2)
On note V1, V2, V3 les modules des vecteurs vitesses, et R1, R2, R3 les angles de ces vecteurs, tous mesurés par rapport au Nord et dans le sens horaire (entre 0° et 360°). Voir Figure ci-dessus.
En projetant la relation vectorielle V3 = V1 + V2 sur les deux axes perpendiculaires Nord et Est, on obtient alors les formules générales suivantes donnant V3 et R3 :
V3 sin(R3) = S = V1 sin(R1) + V2 sin(R2)
V3 cos(R3) = C = V1 cos(R1) + V2 cos(R2)
tg(R3) = S/C
D'où les résultats exacts suivants directement utilisables dans les logiciels :
V32 = S2 + C2 = V12 + V22 + 2 V1 V2 cos(R1 - R2)
R3 en ° = formules suivantes déduites de la convention de repérage des angles, la fonction Arctan[] étant la fonction mathématique classique (comprise entre -90° et +90°).
Cas 1 : Si C > 0 et S ≥ 0 alors : R3 = Arctan[S/C]
Cas 2 : Si C > 0 et S < 0 alors : R3 = Arctan[S/C] + 360°
Cas 3 : Si C < 0 et S quelconque alors : R3 = Arctan[S/C] + 180°
Cas 4 : Si C = 0 et S > 0 alors : R3 = 90°
Cas 5 : Si C = 0 et S = 0 alors : R3 = indéfini (correspondant à V3 = 0)
Cas 6 : Si C = 0 et S < 0 alors : R3 = 270°
Ainsi, pour V1 = (V1, R1) = (10 noeuds, 30°) et V2 = (V2, R2) = (5 noeuds, 70°), on trouve V3 = (V3, R3) = (14 noeuds, 43°).
Sur une calculette, afin d'éviter les divisions par zéro, les calculs se posent comme suit :
Les cas 4 à 6 peuvent être inclus aux cas 1 et 2 en remplaçant C par une constante de vitesse très petite (par exemple ε = 10-3 noeuds) lorsque C = 0
Ce remplacement donne un angle R3 quasi-exact dans les cas 4 et 6. Dans le cas 5, il donne un angle R3 fictif de 0° associé à une vitesse V3 nulle, ce qui n'est pas gênant pour R3 bien qu'inexact.
Les cas 1 à 6 peuvent alors se résumer en une seule formule :
Calcul de S = V1 sin(R1) + V2 sin(R2)
Calcul de C = V1 cos(R1) + V2 cos(R2)
Calcul de C* qui sera toujours non nul = (C - ε) Signe2[C] + ε, correspondant respectivement à C et ε pour C ≠ 0 et C = 0
Signe2[C] = C2 / (C2 + ε2), correspondant respectivement à 1 et 0 pour C ≠ 0 et C = 0
Calcul de V3 = (S2 + C*2)1/2
Calcul de R3 en ° = Arctan[S/C*] + (1 - X) 180°
X = (1/2) (1 + Signe[C*]) (1 + PseudoSigne[S] - PseudoSigne2[S])
Signe[C*] = C* / (C*2)1/2, correspondant respectivement à 1 et -1 pour C* > 0 et C* < 0
PseudoSigne[S] = S / (S2 + ε2)1/2, correspondant respectivement à 1, 0 et -1 pour S > 0, S = 0 et S < 0
Sur une calculette possédant 9 registres mémoire (M1 à M9), les calculs successifs donnant V3 et R3 sont alors les suivants :
M1 = 0,001 = ε
M2 = M12 = ε2
M3 = V1 sin(R1) + V2 sin(R2) = S
M4 = M32 = S2
M5 = V1 cos(R1) + V2 cos(R2) = C
M6 = M52 = C2
M7 = M1 + (M5 - M1) M6 / (M6 + M2) = C*
M8 = M72 = C*2
M9 = M3 / (M4 + M2)1/2 = PseudoSigne[S]
V3 = (M4 + M8)1/2
X = (1/2) (M7/(M8)1/2 + 1) (M9(1 - M9) + 1)
R3 en ° = Arctan[M3/M7] + (1 - X) 180°
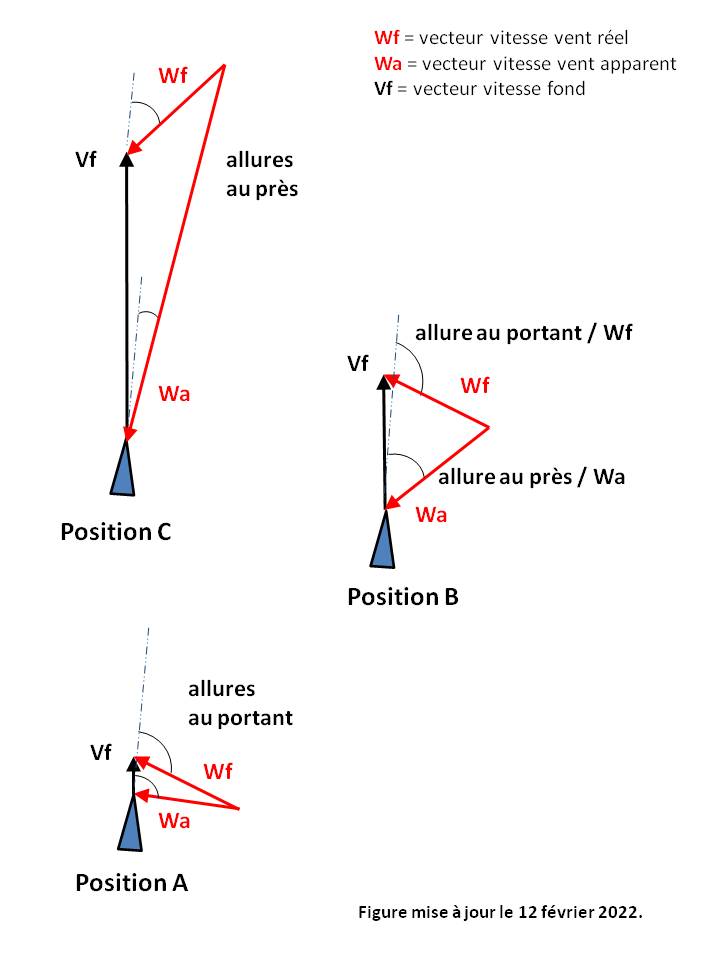
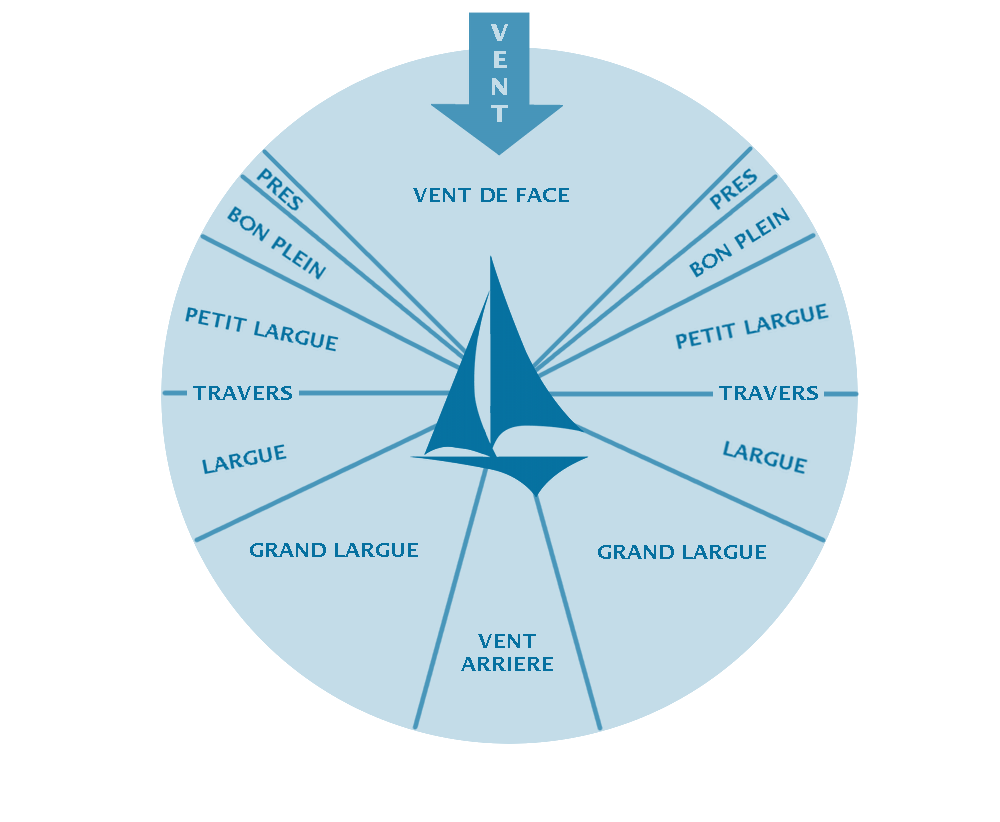
Sur un voilier qui progresse à l'aide de ses voiles, l'allure est l'angle de la Ligne de foi du voilier par rapport à la direction (-Wa ou -Wf) d'où provient le vent (voir Figure 1 ci-dessus).
|
Attention : Deux définitions différentes existent pour ce vent de référence : - Dans la théorie, c'est le Vent réel (Wf), donné par exemple par la direction des rides sur l'eau. - En pratique, c'est le Vent apparent (Wa), donné par exemple par la direction de la girouette ou du drapeau sur le bateau. Lorsque la vitesse du voilier est petite par rapport à la vitesse du Vent réel, les deux définitions se rejoignent. Dans cette page, sauf indication contraire, c'est la seconde définition qui est utilisée : allure par rapport au Vent apparent (cf [Wikipedia, Allure]). |
On distingue les allures suivantes (cf [Wikipedia, Allure]). Voir Figure 2 ci-dessus.
- "Vent debout" ou "Bout au vent" ou "Face au vent" (de 0° à 40° environ), allure pour laquelle le voilier ne peut pas avancer,
- "Près serré" ou "Au plus près" (40°), allure lente avec gîte importante, la meilleure pour remonter le vent,
- "Près bon plein" (de 40° à 60°), allure confortable pour le marin pour laquelle la vitesse du voilier augmente notablement et la gîte diminue.
- "Petit largue" (de 60° à 90°), allure souvent optimale tant du point de vue de la vitesse du voilier que du confort du marin.
- "Vent de travers" (90°), allure rapide avec gîte quasi-nulle, la préférée des débutants,
- "Largue" (de 90° à 120°), allure rapide,
- "Grand largue" (de 120° à 150°), allure la plus rapide pour laquelle l'écoulement des filets d'air sur les voiles n'est plus laminaire mais perturbé, avec apparition de Roulis.
- "Vent arrière" (de 150° à 180°), allure pour laquelle la vitesse du voilier diminue notablement et le Roulis s'accentue.
Les allures sont symétriques. Pour les distinguer, on utilise les termes de "tribord amures" lorsque le bateau reçoit le vent par tribord (droite) et "bâbord amures" dans la situation inverse.
Les termes "près" et "portant" regroupent un ensemble d'allures : le près quand le voilier remonte le vent (allures de Travers à Vent debout) et le portant quand le vent vient de l'arrière (allures de Travers à Vent arrière).
Le terme anglophone "reaching", très employé en course, regroupe les allures de travers : Petit largue, Travers et Largue, correspondant à l'allure la plus favorable pour le bateau.
A noter :
- Un multicoque de course peut démarrer aux allures portantes et, sans changer de cap, se retrouver au près (voir Figure 1 ci-dessus, de la position A à la position B). En prenant de la vitesse, le multicoque voit en effet son vent apparent se renforcer et se rapprocher en direction de l'axe du navire. Il se retrouve ainsi au près alors que le vent réel souffle sur son arrière (cf [Wikipedia, Allure]).
- Tout voilier ne peut pas dépasser le vent apparent qui est son moteur. En revanche, il peut dépasser le vent réel s'il est conçu pour aller vite (cas des multicoques de course et de certains quillards de régate) et en naviguant au près (voir Figure 1 ci-dessus, positions B et C pour lesquelles ||Vf|| > ||Wf||).
- Si la destination du voilier est choisie, l'allure est imposée par la direction que prend le vent durant la navigation et le louvoyage sera souvent nécessaire. Toutefois, si l'équipage du voilier dispose de temps ou si le bateau n'a pas la capacité de tenir l'allure imposée par le vent, il sera souvent possible de choisir une route permettant de bénéficier des allures les plus favorables (les allures portantes).
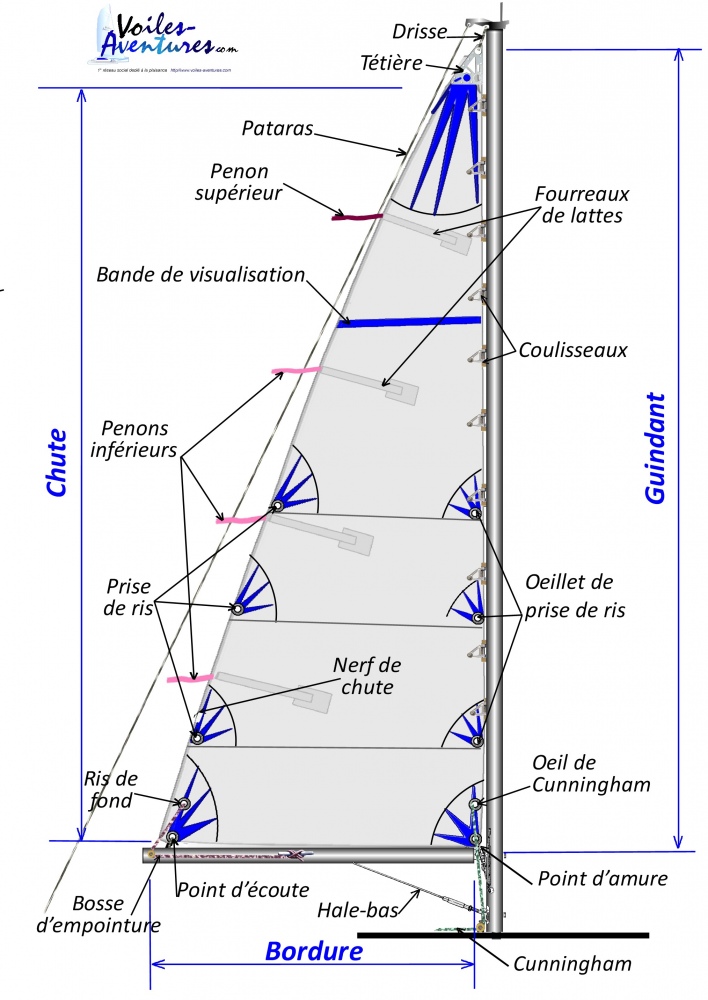
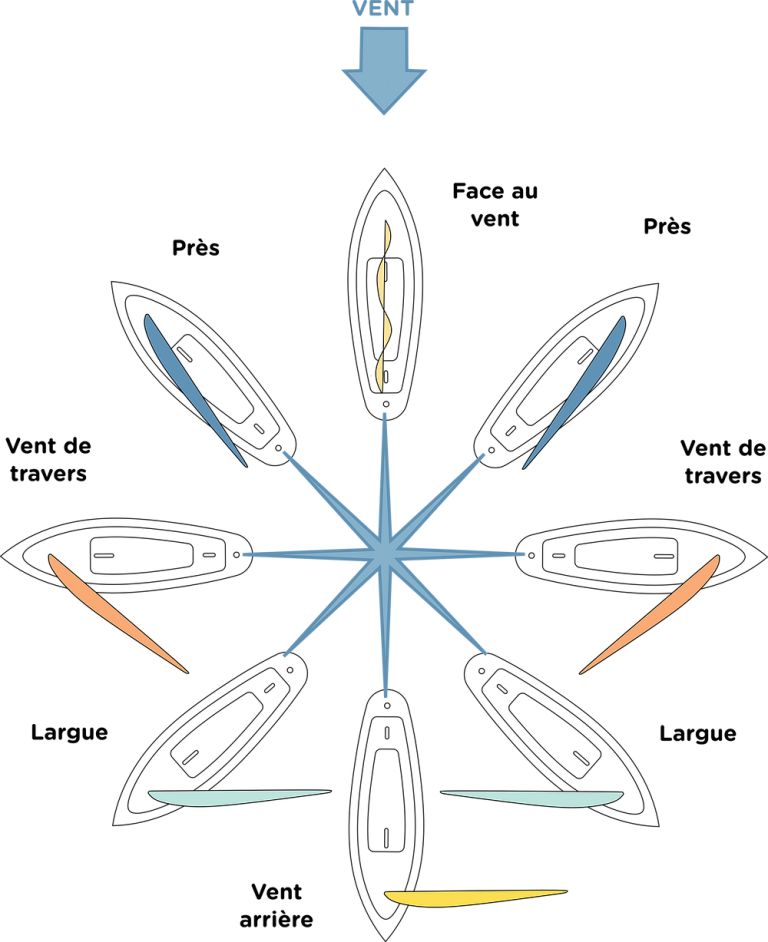
Sur un voilier, le réglage de la voilure consiste à modifier l'orientation et la forme des voiles en fonction de la force et de la direction du Vent apparent, ainsi que de l'état de la mer.
L'objectif est que le voilier puisse avancer le plus rapidement possible ou soit capable de manoeuvrer (virement de bord) :
- soit en disposant d'une force propulsive maximale,
- soit en disposant du meilleur compromis force propulsive / force latérale faisant gîter (pencher) le voilier.
Le réglage doit être revu :
- au fur et à mesure que le bateau "abat" (s'éloigne du vent) ou "lofe" (se rapproche du vent),
- lorsque la direction ou la force du vent se modifie,
- lorsque l'état de la mer évolue (vagues plus fortes ou plus creuses ou changement d'orientation des vagues).
La Grand-Voile (GV) est la voile la plus importante du voilier et se règle comme suit (voir Figure 1 ci-dessus) :
1. Réglage du creux : il se fait en agissant sur la tension de la drisse (cf [DUTHIL]).
2. Réglage de l'Angle d'incidence : il se fait en agissant sur la position du chariot d'écoute (traveller) qui modifie l'angle entre la voile et l'axe du voilier (cf [DUTHIL]).
Aux Allures de près, l'écoulement d'air sur la voile est laminaire. L'Angle d'incidence est maintenue à 20° environ pour bénéficier d'une force aérodynamique maximale (cf [Wikipedia, Théorie du déplacement]). Voir Figure 2 ci-dessus.
Aux Allures portantes, l'écoulement est perturbé et la portance devient négligeable. L'Angle d'incidence est maintenue autour de 90° pour bénéficier d'une trainée propulsive maximale (cf [Wikipedia, Théorie du déplacement]). Voir Figure 2 ci-dessus.
3. Réglage du vrillage (permettant d'assurer un Angle d'incidence constant sur toute la hauteur de la voile) : il se fait en agissant sur la tension du cunningham, la tension de bordure, la tension d'écoute, la tension du hale-bas de bôme et le pataras (cf [DUTHIL]).
La Voile d'Avant (VA) ou foc ou génois, située à l'avant de la grand-voile, vient en association avec la grand-voile comme suit :
Le foc, en raison du couloir entre celui-ci et la grand-voile, accélère les filets d'air sur l'extrados de la grand-voile, retardant son point de décollement éventuel et permettant ainsi d'admettre des Angles d'incidence plus grands. Le foc joue ainsi le rôle d'un bec d'attaque sur une aile d'avion (cf [ENSEEIHT]).
En retour, la présence de la grand-voile derrière le foc améliore l'écoulement de l'air sur l'extrados du foc par aspiration des particules fluides et retarde ainsi le point de décollement éventuel du foc. La grand-voile joue ainsi le rôle d'un volet du bord de fuite sur une aile d'avion (cf [ENSEEIHT]).
Le foc se règle alors comme suit (cf [DUTHIL]) :
1. Réglage du creux : il se fait en agissant sur la tension de la drisse.
2. Réglage de l'Angle d'incidence : il se fait en agissant sur la position du chariot d'écoute (roller) qui modifie globalement la distance d'écartement entre le foc et la grand-voile.
3. Réglage du vrillage : il se fait en agissant sur la tension d'écoute.
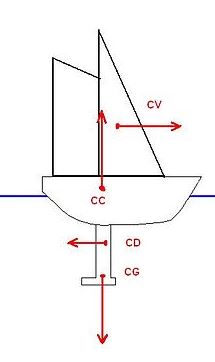
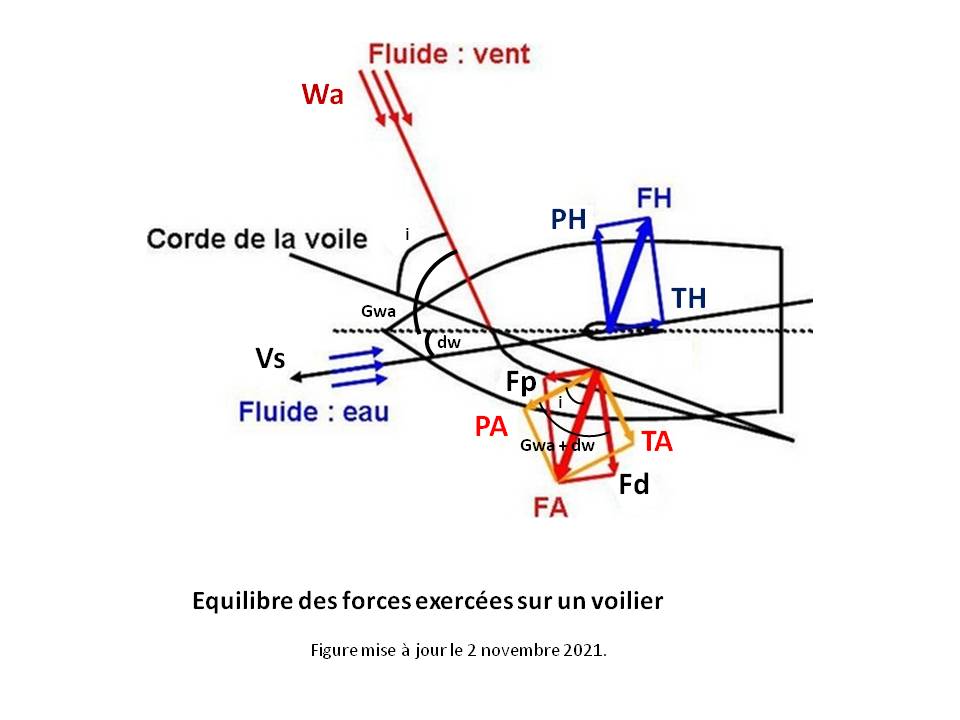
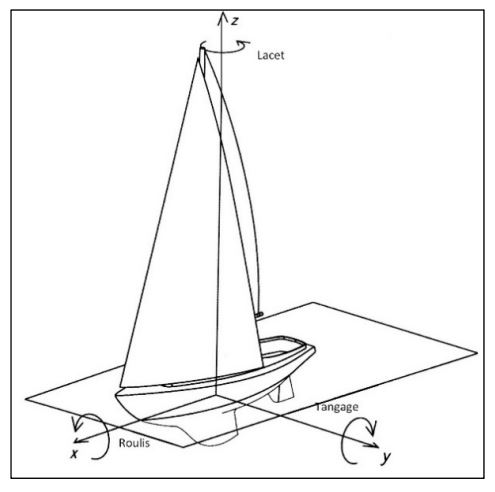
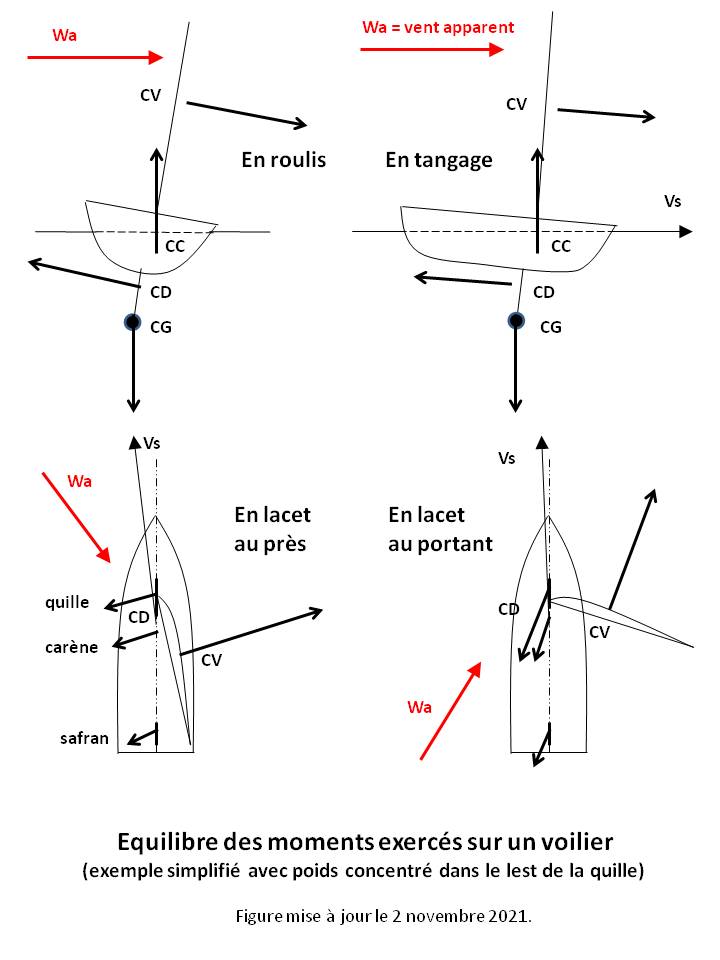
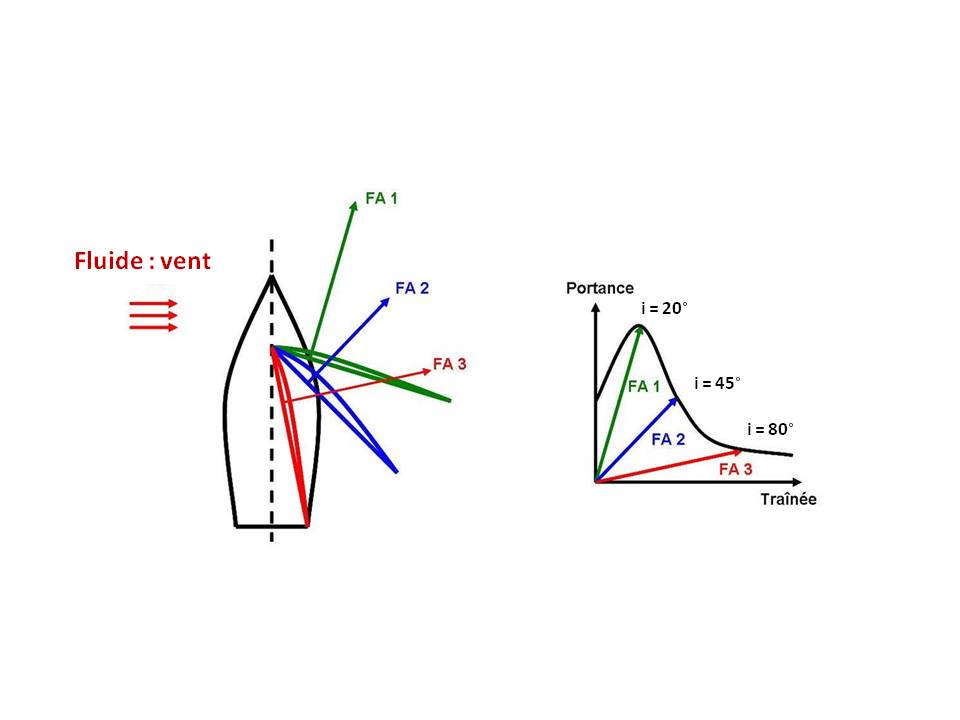
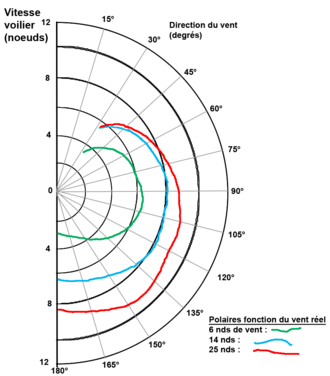
Bilan des forces :
Lorsqu'un voilier est à l'arrêt sans vent, il est équilibré selon la même verticale par deux forces d'intensité égale et de sens opposé (voir Figure 1 ci-dessus, cf [Wikipedia, Equilibre d'un navire sous voiles]) :
- le poids du voilier, appliqué au centre de gravité (CG) qui est le barycentre des forces de pesanteur s'exerçant sur toutes les parties immergées et émergées du voilier.
- la force hydrostatique ou poussée d'Archimède, appliquée au centre de carène (CC), ou centre de poussée ou centre de flottabilité, qui est le centre du volume d'eau déplacé par la carène.
Lorsque le voilier est en mouvement horizontal, il subit en plus les deux forces suivantes (voir Figure 1 ci-dessus) :
- la Force Aérodynamique (FA), dont la force vélique (force des voiles seules) s'applique au centre de voilure (CV) qui est le barycentre des forces aérodynamiques s'exerçant sur chaque voile du voilier.
- la Force Hydrodynamique (FH), appliquée au centre de dérive (CD), ou centre anti-dérive, qui est le barycentre des forces hydrodynamiques s'exerçant sur chaque partie des Oeuvres vives du voilier et qui se trouve grossièrement, pour chaque plan du voilier (vertical longitudinal, vertical transversal, horizontal), au centre de la surface des Oeuvres vives projetée sur ce plan.
Les quatre centres sont tous différents.
Attention : Il est parfois écrit, de façon erronée, que la force hydrodynamique (FH) s'applique au centre de carène (CC).
La Force Aérodynamique FA (voir Figure 2 ci-dessus, cf [Culture maritime, La décomposition des FA et FH au près]) :
FA est la résultante des forces induites par le vent sur l'ensemble des Oeuvres mortes du voilier.
En première approximation, on peut négliger les forces exercées par le vent sur le voilier nu (hors voilure) et ne considérer que les forces des voiles (cf [Wikipedia, Equilibre d'un navire sous voiles]).
FA se réduit alors à la force vélique Fv, résultante des forces induites par le vent dans la voilure (ensemble de toutes les voiles). Fv s'applique au centre de voilure (CV).
Sur chaque voile, le vent exerce une surpression sur son intrados (points situés au vent) et une dépression sur son extrados (points situés sous le vent). La force résultante est quasi-perpendiculaire à la corde de la voile pour les Angles d'incidence supérieurs à 25°.
Sur la voilure complète, FA se décompose alors aérodynamiquement en trois forces (cf [Wikipedia, Effort sur une voile]) :
- la Trainée Aérodynamique (TA), qui est parallèle à la direction Wa du vent apparent,
- la Portance Aérodynamique (PA), qui est perpendiculaire à Wa dans le plan horizontal.
- la Portance aérodynamique Latérale, qui est perpendiculaire à Wa selon la verticale, et négligeable en première approximation.
Selon l'Angle d'incidence (i), la portance ou la trainée aérodynamique peut être le facteur propulsif prédominant (mode aile ou mode parachute).
La Force Hydrodynamique FH (voir Figure 2 ci-dessus) :
FH est la résultante des forces induites par l'eau sur l'ensemble des Oeuvres vives du voilier dans son mouvement par rapport à l'eau. FH s'applique au centre anti-dérive (CD).
FH se décompose mécaniquement en trois forces :
- la résistance à l'avancement, ou Trainée Hydrodynamique TH, qui est parallèle au vecteur Vitesse surface Vs du voilier.
- la résistance à la dérive, ou Portance Hydrodynamique PH, qui est perpendiculaire à TH dans le plan horizontal.
- la résistance à l'enfoncement, ou Portance hydrodynamique Latérale, qui est perpendiculaire à TH selon la verticale, et négligeable en première approximation.
La Trainée Hydrodynamique TH intègre quatre résistances différentes (cf [Wikipedia, Traînée]) : la résistance de pression (due à la forme de la carène), la résistance visqueuse (due au frottement), la résistance d'onde (due à la génération des vagues d'accompagnement) et la résistance induite par la portance (due aux tourbillons en bout de carène).
Equilibre dans le plan horizontal :
Sous réserve des trois approximations faites ci-dessus, un voilier en mouvement à vitesse constante (donc sans accélérations, ni décélérations dues notamment aux vagues de la houle venant buter sur la coque) est équilibré dans le plan horizontal par les deux forces FA et FH d'intensité égale et de sens opposé.
FA peut alors se décomposer mécaniquement en deux forces horizontales (voir Figure 2 ci-dessus) :
- la Force propulsive (Fp), ou force d'avancement, qui est égale en intensité et opposée en sens à la Trainée Hydrodynamique TH, donc parallèle au vecteur Vitesse surface Vs du voilier.
- la Force de dérive (Fd) qui est égale en intensité et opposée en sens à la Portance Hydrodynamique PH, donc perpendiculaire à Vs.
Les moments de redressement :
La force aérodynamique s'exerçant sur le voilier en mouvement génère par ailleurs trois moments perturbateurs autour des axes de Roulis, de Tangage et de Lacet (voir Figure 3 ci-dessus).
Les autres forces (poids, force hydrostatique et force hydrodynamique) développent alors trois moments de redressement (ou de rappel) qui maintiennent le voilier en équilibre comme suit (voir Figure 4 ci-dessus) :
- En Roulis, le moment de redressement transversal s'oppose au moment de chavirage et maintient le voilier en équilibre selon une gîte constante. Si le moment de la force hydrostatique en CC par rapport au centre de gravité CG ne suffit pas pour maintenir l'équilibre, une solution consiste à ajouter un poids fixe (par exemple, le lest de quille ou des ballasts que l'on remplit) ou un contre-poids variable selon les Allures (par exemple, le marin en position de trapèze).
- En Tangage, le moment de redressement longitudinal s'oppose au moment de piqué (ou d'enfournement) et maintient le voilier en équilibre selon une assiette constante. Par construction du voilier, le moment de la force hydrostatique en CC par rapport au centre de gravité CG suffit pour maintenir l'équilibre.
- En Lacet, le moment de redressement horizontal s'oppose au moment de virage et maintient le voilier en équilibre selon une dérive constante. L'équilibre en Lacet est réalisé (cf [PALLU]) avec une répartition appropriée de la portance hydrodynamique entre les différents appendices (quille, safran, etc.), le safran permettant d'influer sur le Lacet pendant la navigation.
En principe, un voilier parfaitement équilibré maintiendra une route bien droite, sans l'aide du gouvernail. En réalité, pour des raisons de sécurité, la majorité des voiliers sont dessinés et réglés pour être légèrement ardents au près (avec un centre de dérive CD légèrement en avant du centre de voilure CV). Si la barre est laissée à elle-même, automatiquement le voilier lofera et s'arrêtera vent debout.
Conséquences pratiques :
|
L'intensité de la force aérodynamique (FA) est d'autant plus grande que : 1. la vitesse du Vent apparent (Wa) est grande, 2. l'Angle d'incidence (i) est proche de 20° ou de 80°. Voir graphique en Figures 5 et 6 ci-dessus (cf [Culture maritime, La polaire d'une voile selon l'angle d'incidence]). 3. la forme de la voile est cambrée (avec creux important), 4. la surface de la voile est grande, 5. l'allongement de la voile (rapport entre carré de la hauteur et surface) est grand. L'intensité de la force propulsive (Fp) vaut : Fp = FA sin(Gwa + dw - i), Gwa étant le Gisement vent apparent du voilier, dw la Dérive vent et i l'Angle d'incidence de la voile (voir Figure 2 ci-dessus). En conséquence, cette intensité est d'autant plus grande que : 1. l'intensité de la force aérodynamique (FA) est grande, 2. pour une même vitesse du Vent apparent (Wa), le Gisement vent apparent (Gwa) est proche de la valeur (90° + i - dw), c'est-à-dire aux Allures portantes Largue et Grand largue. L'intensité de la vitesse de surface (Vs), pour un voilier donné (coque et voilure), est donné par ses polaires de vitesse en fonction de la force et de la direction du Vent réel. La Figure 7 ci-dessus donne l'exemple des polaires de vitesse d'un voilier quillard de croisière de 30 pieds pour trois vitesses de vent. Sa vitesse maximale est atteinte pour une direction de Vent réel comprise entre 120° et 150°, et vaut respectivement (6, 8, 9) noeuds pour une force de vent de (6, 14, 25) noeuds (cf [Wikipedia, Polaire des vitesses]). |
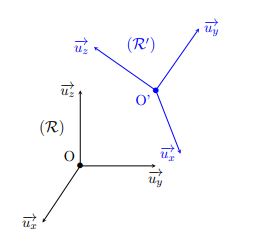
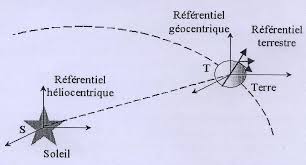

Lorsque le référentiel d'étude n'est pas galiléen, la relation fondamentale de la dynamique fait apparaître des termes spécifiques à ce problème sous forme de forces virtuelles dont notamment la force centrifuge et le force de Coriolis. Explication (cf [Physagreg]) :
On considère un référentiel fixe R (référentiel galiléen de centre O) et un référentiel R' mobile (référentiel non galiléen de centre O') animé d'un mouvement quelconque par rapport à R (voir Figure 1 ci-dessus).
Par exemple (voir Figure 2 ci-dessus), si R est le référentiel héliocentrique (de centre S et d'axes stellaires), Rg le référentiel géocentrique (de centre T et d'axes stellaires) et R' le référentiel terrestre (de centre T et d'axes attachés au globe terrestre), alors le mouvement de R' par rapport à R est une rotation de R' dans Rg, lui-même en translation circulaire dans R.
Le vecteur ΩR'/R représente la rotation de R' dans R.
Edmond Bour (mathématicien français, 1832-1866, voir Figure 3 ci-dessus) a établi une formule valable pour tout R' en mouvement quelconque par rapport à R, qui permet de relier la variation dans le temps t de tout vecteur X dans R avec celle de ce même vecteur dans R' :
(R1) (dX/dt)R = (dX/dt)R' + ΩR'/R x X
Le symbole "x" représentant le produit vectoriel.
Si OM est le vecteur position d'un point M quelconque dans R, alors on peut écrire :
(R2) OM = OO' + O'M
Soient v et Γ les vecteurs vitesse et accélération du point M.
En dérivant dans R la relation (R2) par rapport au temps t, et en appliquant la formule de Bour (R1) au vecteur O'M, on obtient alors :
(R3) va = vr + ve
avec :
vitesse absolue (va) = (dOM/dt)R = vMR
vitesse relative (vr) = (dO'M/dt)R' = vMR'
vitesse d'entraînement (ve) = vO'R + ΩR'/R x O'M
En dérivant dans R la relation (R3) par rapport à t, et en appliquant la formule de Bour (R1) aux vecteurs vMR' et dO'M/dt, on obtient ensuite :
(R4) Γa = Γr + Γe + Γc
avec :
accélération absolue (Γa) = (dvMR/dt)R = ΓMR
accélération relative (Γr) = (dvMR'/dt)R' = ΓMR'
accélération d'entraînement (Γe) = ΓO'R + d(ΩR'/R)/dt x O'M + ΩR'/R x (ΩR'/R x O'M)
Γe se composant de trois termes d'accélération : le premier lié à la translation, le second à la dérivée du vecteur rotation, le troisième au vecteur rotation (accélération centrifuge).
accélération de Coriolis (Γc) = 2 ΩR'/R x vMR'
Dans ce cas, on a : ΩR'/R = 0, ce qui donne :
ve = vO'R
Γe = ΓO'R
Γc = 0
Dans ce cas, on a : O' = O et d(ΩR'/R)/dt = 0, ce qui donne :
ve = ΩR'/R x O'M
Γe = ΩR'/R x (ΩR'/R x O'M)
Γc = 2 ΩR'/R x vMR'
Si H est le point projeté de M sur l'Axe de rotation, alors on peut aussi écrire :
(R5) Γe = -(ΩR'/R)2 HM
Dans le référentiel galiléen R, la relation fondamentale de la dynamique appliquée au point M de masse m s'écrit :
(R6) Résultante des forces (ΣF) = m (ΓR)
Compte tenu de la relation (R4), cela peut s'écrire :
(R7) ΣF - m Γe - m Γc = m ΓR'
Dans le référentiel non galiléen R', la relation fondamentale de la dynamique devient alors :
(R8) ΣF + Fie + Fic = m ΓR'
avec :
force d'inertie d'entraînement (Fie) = -m Γe
force d'inertie de Coriolis (Fic) = -m Γc
Ces deux forces sont dites virtuelles ou apparentes, car causées par le caractère non galiléen du référentiel R'.
Dans le cas d'un mouvement R'/R de rotation uniforme autour d'un axe fixe, compte tenu de la relation (R5), la force d'inertie d'entraînement vaut : Fie = m (ΩR'/R)2 HM et s'appelle force centrifuge ressentie par M au cours de son mouvement de rotation.
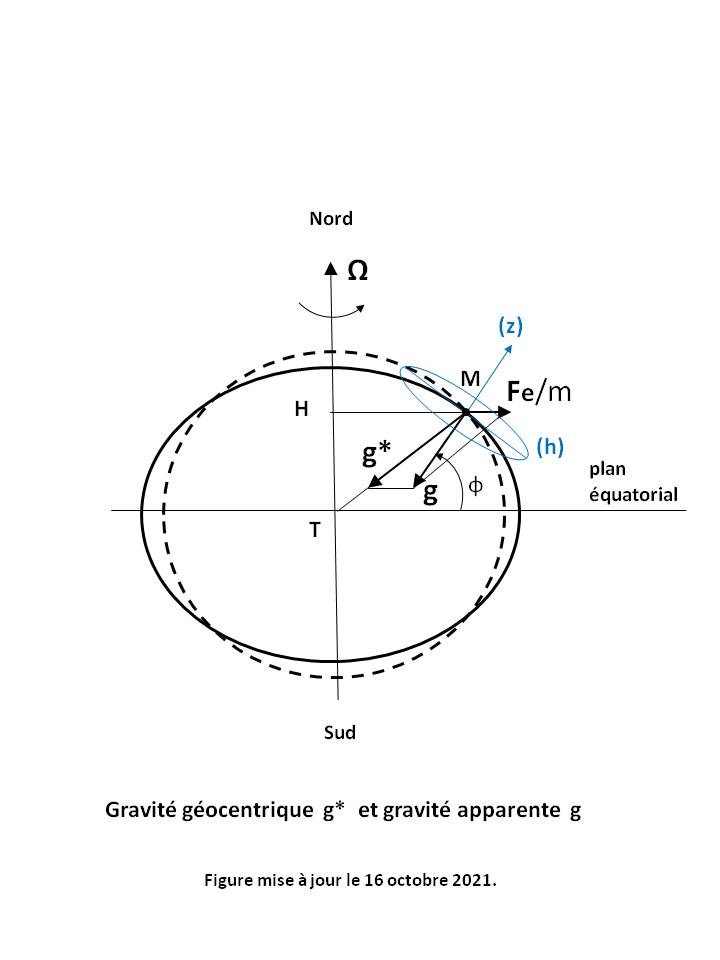
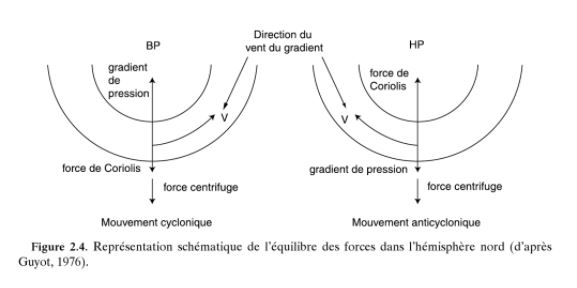
Le vent géostrophique est une approximation commune en météorologie. C'est le Vent en altitude pour lequel la force d'inertie de Coriolis équilibrerait exactement les forces de pression.
Le vent synoptique est le Vent des cartes météo de surface. C'est le Vent au sol, sans Reliefs importants et à grande échelle de la circulation atmosphérique terrestre (étendue de l'ordre de 1000 km). Il se déduit du calcul du vent géostrophique en prenant aussi en compte, dans la couche limite atmosphérique, l'effet de la friction sur les faibles Reliefs.
Dans le Système géodésique standard, le globe terrestre est assimilable à une ellipsoïde de révolution qui tourne sur elle-même. Les notations sont les suivantes (voir Figure 1 ci-dessus) :
T est le Centre des masses de la Terre.
M est un point quelconque de l'atmosphère terrestre.
Φ est la Latitude géographique (ou géodésique ou ellipsoïdale) du point M. Attention à ne pas confondre avec la Latitude géocentrique φ ou la Latitude astronomique.
Ω est le vecteur rotation, situé sur l'Axe de rotation de la Terre, orienté Sud-Nord et supposé constant en direction et en module (Ω = 7,3 10-5 rad/s).
(z) est l'axe vertical ascendant du point M (perpendiculaire à la surface de la Terre).
(h) est le plan horizontal en M (parallèle à la surface de la Terre).
g est l'accélération de la pesanteur au niveau de la mer (g = 9,81 m/s2 à Paris).
z est l'Altitude (ou hauteur) du point M par rapport au niveau de la mer.
H est le point projeté de M sur l'Axe de rotation de la Terre.
a est le rayon équatorial (ou demi-grand axe de l'Ellipsoïde de référence) valant : a = 6 378,137 000 km (cf modèles WGS84 et GRS 80).
b est le rayon polaire (ou demi-petit axe de l'Ellipsoïde de référence) valant : b = 6 356,752 314 245 km (cf modèle WGS84).
f = (a - b)/a est l'aplatissement géométrique valant : f = 1/298,257 223 563 (cf modèle WGS84).
e = (a2 - b2)1/2/a est la première excentricité valant : e = 0,081 819 190 842 (cf modèle WGS84).
ρ = a (1 - e2) / w3 est le rayon de courbure local dans le Plan méridien en un point de Latitude géocentrique φ (cf [IGN][BOSSER]).
N = a / w est le rayon de courbure local dans le plan du Parallèle en un point de Latitude géocentrique φ (cf [IGN][BOSSER]).
avec : w = (1 - e2 sin2(φ))1/2 (cf [IGN][BOSSER]).
R = (ρ N)1/2 = a (1 - e2)1/2 / w2 = b/w2 est le rayon de la sphère qui se rapproche au mieux de l'Ellipsoïde de référence en un point de Latitude géocentrique φ (cf [IGN][BOSSER]).
"grad()", "rot()", "x", Δ() et div() sont respectivement les opérateurs "gradient", "rotationnel", "produit vectoriel", "laplacien vectoriel" et "divergence".
t est le temps.
Γ, v et m sont respectivement le vecteur accélération, le vecteur vitesse et la masse de la particule M.
r est la masse volumique du fluide avec : rair sec = 1,23 kg/m3 en conditions standard au niveau de la mer (température de 15 °C et pression de 1 atm = 1013,25 hPa).
p est la pression locale du fluide.
η est la viscosité dynamique du fluide (si visqueux) : ηair sec = 1,7 10-5 Pa.s en conditions standard au niveau de la mer.
On considère le référentiel terrestre (de centre T et d'axes attachés au globe terrestre), mobile en rotation par rapport au référentiel géocentrique (de centre T et d'axes stellaires) supposé galiléen (voir Lois de la physique en référentiel non galiléen).
La rotation est supposée uniforme autour d'un axe fixe (axe des Pôles géographiques).
L'atmosphère terrestre liée au globe terrestre est supposée être un fluide parfait (i.e. non visqueux).
Dans le référentiel terrestre (non galiléen), la relation fondamentale de la dynamique appliquée à une particule M de ce fluide dont on suit le mouvement le long de sa trajectoire (description lagrangienne) peut alors s'écrire (voir Bélier hydraulique - Annexe - Equation du mouvement) :
(R1) Γ = dv/dt + (1/2) grad(v2) + rot(v) x v = (ΣF/m) + Fp
(R1p) Fp = -(1/r) grad(p) est l'ensemble des forces de pression ramené à l'unité de masse,
ΣF est l'ensemble des forces actives (motrices) appliquées sur la particule, lesquelles sont les suivantes :
(R1g) Fg, force de gravité, qui vaut : Fg = m grad(-g z) = m g dans le cas de faibles Altitudes z par rapport au rayon de la Terre. Cette force n'est pas dirigée exactement vers le centre de la terre (gravité géocentrique g*) car, sous l'effet combiné de la rotation terrestre (force centrifuge globale) et de la gravitation terrestre (force gravitationnelle), la surface de la Terre s'est ajustée lors de sa formation pour adopter une forme ellipsoïde de révolution dans laquelle le vecteur gravité g (appelé gravité "apparente") est partout perpendiculaire à la surface (voir Figure 1 ci-dessus).
(R1e) Fe, force d'inertie d'entraînement (ou force centrifuge globale), qui vaut : Fe = m (Ω)2 HM. Cette force est due à la rotation de la Terre sur elle-même et est englobée dans la force Fg.
(R1c) Fc, force d'inertie de Coriolis, qui vaut : Fc = -2 m Ω x v. Cette force est due à la rotation de la Terre sur elle-même.
En projetant le vecteur Fc selon la verticale (z) du point M et son plan horizontal (h), on peut écrire : Fc = -2 m (Ωz + Ωh) x (vz + vh) = Fcz + Fch, ce qui donne en développant :
(R1cz) Fcz = -2 m Ωh x vh
(R1ch) Fch = -2 m (Ωz x vh + Ωh x vz)
(R1l) Fl, force centrifuge locale. Cette force est due à la courbure des Isobares (voir Figure 2 ci-dessus) et n'est à considérer que pour certains cas précis (voir Formation des vents).
(R1f) Ff, force de friction. Cette force est due à la viscosité de l'air au niveau du sol et dans la Couche limite atmosphérique, laquelle est nulle dans le cas théorique d'un fluide non visqueux.
La relation (R1) s'écrit finalement :
(R2) Γ = (Fg + Fc)/m + Fp = g - 2 Ω x v - (1/r) grad(p)
En projetant les vecteurs Ω et v sur la verticale (z) du point M et son plan horizontal (h), on a également les relations suivantes :
(R3) Ω = Ωz + Ωh, Ω = ||Ω||, Ωz = ||Ωz|| = Ω sin(Φ) et Ωh = ||Ωh|| = Ω cos(Φ)
(R3') v = vz + vh, vz = ||vz|| et vh = ||vh||
En se donnant une échelle de distance L et une échelle de Vitesse U, on peut estimer l'ordre de grandeur (ODG) des différents termes composant l'accélération Γ comme suit :
- le terme ODG[ dv/dt ] = U / (L/U) = U2/L
- le terme ODG[ (1/2) grad(v2) ] = U2/L
- le terme ODG[ rot(v) x v ] = (U/L) U = U2/L
On se place aux grandes échelles de la circulation atmosphérique terrestre (L = 1000 km) et pour des Vitesses moyennes correspondant à des Vents sans Tempête (U = 10 m/s). Dans ces conditions, on a alors :
(R4) ODG[ Γ ] = U2/L = 10-4 m/s2
La relation (R2) projetée sur la verticale (z) s'écrit :
(R2z) Γz = (Fg + Fcz)/m + Fpz
On considère le ratio d'échelle ΔΓg = ||Γz|| / ||Fg/m|| = ||Γz|| / g.
Compte tenu de (R4), son ordre de grandeur est inférieur à la quantité ODG[ Γ ] / g = 10-5 m/s2
L'accélération verticale Γz de la particule est donc négligeable par rapport à la force de gravité massique Fg/m, ce qui revient à considérer le mouvement vertical de la particule comme rectiligne et uniforme.
La relation (R2z) se réduit alors à :
(R5) 0 = (Fg + Fcz)/m + Fpz
On considère le ratio d'échelle Δcg = ||Fcz|| / ||Fg||.
Compte tenu de (R1cz)(R1g)(R3), ce ratio vaut : 2 Ω cos (Φ) vh |sin(Ωh ; vh)| / g
Pour des Vitesses horizontales vh inférieures à 100 m/s (Tempête), Δcg est toujours inférieur à la quantité 2 Ω vh/g = 10-3.
La composante verticale Fcz de la force d'inertie de Coriolis est donc négligeable par rapport à la force de gravité Fg et la relation (R5) se réduit à :
(R6) 0 = Fg/m + Fpz = g - (1/r) grad(p)z
On reconnaît l'équation de l'équilibre hydrostatique : dp/dz = -r g
Les forces Fcz et Fg étant dirigées selon la verticale (z), la relation (R2) projetée sur le plan horizontal (h) s'écrit alors :
(R2h) Γh = Fch/m + Fph
On considère le ratio d'échelle ΔΓp = ||Γh|| / ||Fph|| = ||Γh|| r/|dp/dh|
Son ordre de grandeur est inférieur à la quantité ODG[ Γ ] r/|dp/dh|
Compte tenu de (R4), et pour une distance horizontale dh = 250 km entre deux Isobares espacés de dp = 5 hPa sur une carte météo, ce ratio est toujours inférieur à 6 10-2.
Dans le plan horizontal, l'accélération Γh de la particule est donc négligeable par rapport aux forces de pression Fph, ce qui revient à considérer le mouvement horizontal de la particule comme rectiligne et uniforme.
Compte tenu de (R1ch), la relation (R2h) se réduit alors à :
(R7) 0 = Fch/m + Fph = -2 Ωz x vh - 2 Ωh x vz + Fph
Attention :"Mouvement horizontal" ne veut pas dire "ignorer la Vitesse verticale vz dans les équations" car cette dernière contribue à la composante horizontale Fch de la force de Coriolis (cf relation (R1ch)).
Pour les Latitudes Φ supérieures à Φ0 = 20°, on considère le ratio d'échelle Δhz = ||Ωh x vz|| / ||Ωz x vh||, qui caractérise la contribution de la Vitesse verticale vz par rapport à celle de la Vitesse horizontale vh dans la composante horizontale Fch (voir relation (R1ch)).
Compte tenu de (R3)(R3'), ce ratio vaut : Δhz = (vz/vh)/tg(Φ)
Pour des Vents à composante horizontale dominante (vz/vh petit), ce ratio est donc également petit et la relation (R7) se réduit à :
(R8) 0 = -2 Ωz x vh + Fph
On reconnaît l'équation de l'équilibre Géostrophique pour lequel, dans le plan horizontal, la force d'inertie massique de Coriolis Fc/m est équilibrée par les forces de pression Fp.
En prenant le produit scalaire de cette relation avec la Vitesse vh, on trouve que : Fph.vh = 0, ce qui montre que les Isobares sont colinéaires à la Vitesse horizontale vh, donc aux lignes de courant.
Par ailleurs, en prenant le produit vectoriel de cette relation avec la vitesse Ωz, on trouve que : Fph x Ωz = -Ωz x (2 Ωz x vh) = -(Ωz.vh) (2 Ωz) + (Ωz.(2 Ωz)) vh = 2 (Ωz)2 vh, ce qui montre que le triplet (Fph, Ωz, vh) forme un trièdre rectangle de sens direct, quel que soit l'hémisphère (Nord ou Sud) et quel que soit le type de centre d'action (Dépression ou Anticyclone).
Le Vent souffle donc parallèlement aux lignes Isobares et laisse à sa gauche les régions de basse pression dans l'hémisphère nord ou de haute pression dans l'hémisphère sud (voir Figure 2 ci-dessus).
L'intensité vh du Vent horizontal vh vaut alors :
(R9) vh = (1/r) |dp/dh| / (2 Ω sin(Φ))
Ainsi, pour une distance horizontale dh = 250 km entre deux Isobares espacés de dp = 5 hPa sur une carte météo, dans une région de Latitude Φ = 45°, le Vent soufflera avec une Vitesse horizontale de 15 m/s, soit environ 54 km/h.
Pour les faibles Latitudes (Φ < Φ0), compte tenu de (R3), la composante Ωz est quasi-nulle et la relation (R7) se réduit à :
(R10) 0 = -2 Ωh x vz + Fph
On considère le ratio d'échelle Δzp = ||2 Ωh x vz|| / ||Fph||
Compte tenu de (R3), ce ratio vaut : Δzp = 2 Ω cos(Φ) vz r/|dp/dh|
Pour une distance horizontale dh = 250 km entre deux Isobares espacés de dp = 5 hPa sur une carte météo et un Vent vertical vz de l'ordre de 0,1 m/s, Δzp est toujours inférieur à la quantité 2 Ω vz r/|dp/dh| = 10-2.
Dans le plan horizontal, la force d'inertie de Coriolis est donc quasi-nulle relativement aux forces de pression et seule la force centrifuge locale Fl due à la courbure des Isobares peut maintenir un équilibre avec les forces de pression. En particulier (cf [DE PARCEVAUX]) :
- Dans le cas d'un Anticyclone, l'équilibre est instable (voir Figure 2 ci-dessus, cas du centre Haute Pression (HP) en hémisphère nord). Dès qu'un maximum de pression apparaît (par exemple par affaissement d'une masse d'air), le Vent passe à travers les Isobares et le vide rapidement.
- Dans le cas d'une Dépression, l'équilibre est stable (voir Figure 2 ci-dessus, cas du centre Basse Pression (BP) en hémisphère nord). C'est pourquoi il existe une ceinture permanente de basses pressions au voisinage de l'Equateur.
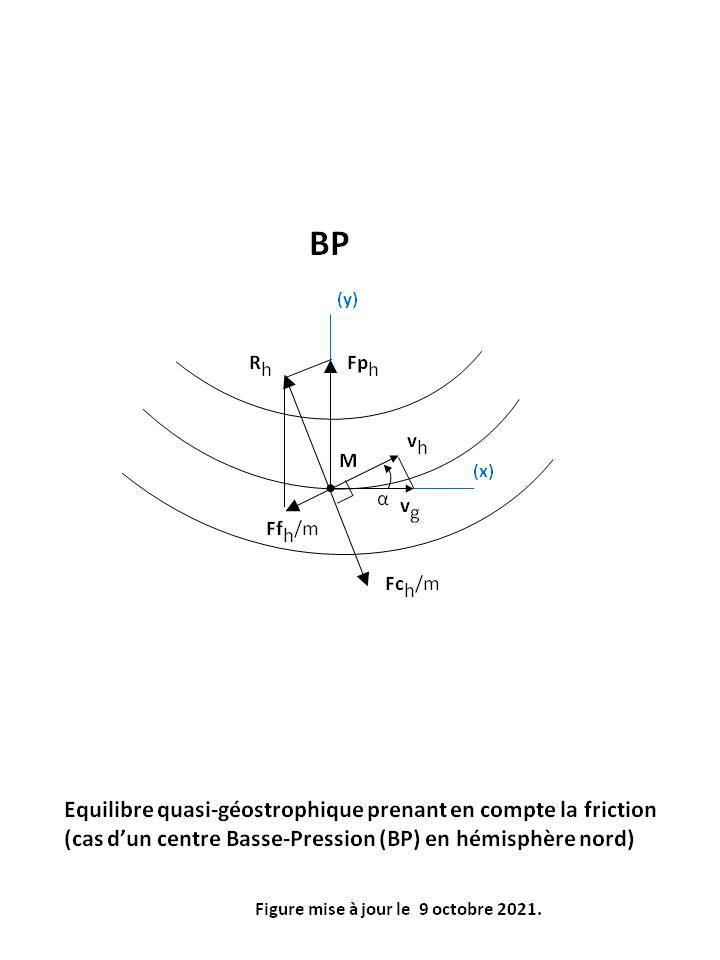
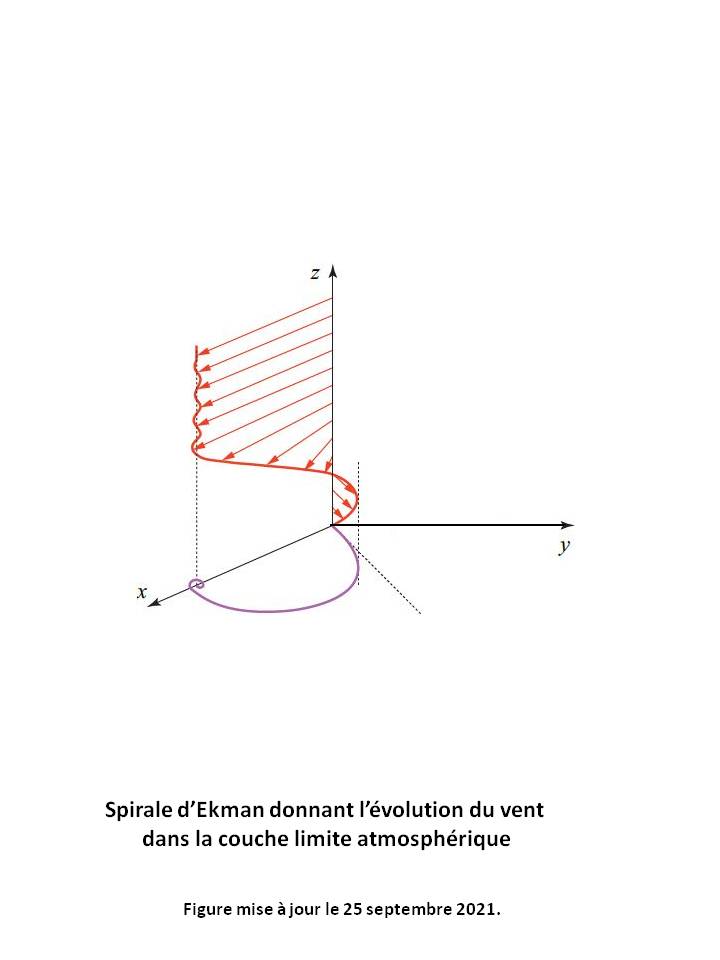
Lorsque la particule d'air se situe dans la Couche limite atmosphérique, il faut considérer la viscosité de l'air et rajouter la force de friction Ff dans la relation (R1).
Si l'on ne cherche pas à connaître le détail du profil du Vent synoptique dans cette couche en fonction de l'Altitude (spirale d'Ekman), la force de friction qui s'exerce globalement sur la particule d'air est une force qui s'oppose à son mouvement (cf [PICCA, p.661]) et vaut :
(R11) Ff = -m k v
où k est un coefficient positif supposé constant à une Altitude donnée.
L'équation (R8) du mouvement horizontal de la particule hors zone équatoriale devient alors :
(R12) 0 = -2 Ωz x vh + Rh
avec : Rh = Fph + Ffh/m
On reconnaît l'équation d'un équilibre quasi-Géostrophique pour lequel, dans le plan horizontal, la force d'inertie massique de Coriolis Fc/m est équilibrée par la résultante R des forces de pression Fp et de friction Ff/m (voir Figure 1 ci-dessus, cas du centre Basse Pression (BP) en hémisphère nord).
En prenant le produit scalaire de cette relation avec la Vitesse vh, on trouve que : Rh.vh = 0, donc que : Fph.vh = k ||vh||2 > 0, ce qui montre que la Vitesse horizontale vh fait un angle (α) par rapport aux Isobares, dirigé vers le vecteur Fph (voir Figure 1 ci-dessus).
Par ailleurs, en prenant le produit vectoriel de cette relation avec la vitesse Ωz, on trouve que : Rh x Ωz = 2 (Ωz)2 vh, ce qui montre que le triplet (Rh, Ωz, vh) forme un trièdre rectangle de sens direct.
Le Vent souffle donc selon un angle (α) par rapport aux lignes Isobares, dirigé vers les pressions décroissantes, et en laissant à sa gauche les régions de basse pression dans l'hémisphère nord ou de haute pression dans l'hémisphère sud (voir Figure 1 ci-dessus).
Compte tenu de la relation géométrique : ||Fch/m|| = ||Rh|| = ||Fph|| cos(α), l'intensité vh du vent du Vent horizontal vh vaut alors :
(R13) vh = (1/r) |dp/dh| cos(α) / (2 Ω sin(Φ))
En conclusion, par rapport au Vent géostrophique, la friction a donc pour effet de diminuer l'intensité du Vent et de modifier sa direction selon un angle rentrant dans la Dépression et sortant de l'Anticyclone.
Si l'on cherche à connaître le détail du profil du Vent synoptique dans la Couche limite atmosphérique en fonction de l'Altitude, le modèle de la "spirale d'Ekman" fournit une bonne approximation qui se détermine comme suit (cf [WILSON][UVED]) :
Pour un fluide en mouvement de type atmosphère terrestre visqueuse, la viscosité à considérer ne dépend pas des caractéristiques du fluide (notamment sa viscosité cinématique ν = η/r qui est de l'ordre de 10-5 m2/s) mais de l'Altitude de la particule et des caractéristiques de l'écoulement (via le coefficient K de viscosité turbulente qui est de l'ordre de 10 m2/s) (cf [WILSON, p.51 et 53]).
L'expression générale de la force de friction Ff s'écrit alors (cf [WILSON, p.54]) :
(R14) Ff = m K Δ(v)
où K est le coefficient de viscosité turbulente, déterminé expérimentalement et supposé constant sur toute l'épaisseur de la Couche limite atmosphérique.
En supposant le gradient horizontal de pression (dp/dh) constant aussi sur toute l'épaisseur de la Couche limite atmosphérique, la relation (R8) s'écrit pour toute Altitude z hors zone équatoriale :
(R15) Fph = 2 Ωz x vg
où vg est la vitesse vh du Vent géostrophique.
Compte tenu de (R14)(R15), la relation (R12) donnant le mouvement horizontal de la particule hors zone équatoriale devient alors :
(R16) 0 = 2 Ωz x (vg - vh) + K Δ(vh)
En projetant cette relation sur l'axe orienté (x) porté par vg et sur l'axe orienté (y) porté par les forces de pression horizontales Fph (voir Figure 1 ci-dessus), on trouve alors :
(R16x) (0 = Γx) = 2 Ωz vy + K (d2vx/dx2 + d2vx/dy2 + d2vx/dz2)
(R16y) (0 = Γy) = 2 Ωz (vg - vx) + K (d2vy/dx2 + d2vy/dy2 + d2vy/dz2)
En faisant l'hypothèse d'un sol relativement plat (Reliefs faibles), le flux d'air est homogène horizontalement (dvx/dx = dvx/dy = dvy/dx = dvy/dy = 0) et les relations (R16x)(R16y) se simplifient comme suit :
(R17x) 0 = 2 Ωz vy + K d2vx/dz2
(R17y) 0 = 2 Ωz (vg - vx) + K d2vy/dz2
En posant : w = vx + i vy et en additionnant ces relations sous la forme complexe (R17x) + i (R17y), on obtient alors :
(R18) 2 Ωz i (w - vg) = K d2w/dz2
En posant : b = (Ωz/K)1/2 et a = b(1 + i), cette relation est équivalente à :
(R19) d2w/dz2 - a2 w = - a2 vg
et s'intègre comme suit :
(R20) w = vg + A ea z + B e-a z
Loin du sol (z = +∞), on tend vers la solution géostrophique (w = vg), ce qui impose : A = 0.
Au sol (z = 0), le Vent est nul (w = 0), ce qui impose : B = -vg
D'où le résultat :
(R21) w = vx + i vy = vg (1 - e-b z e-i b z) = vg (1 - e-b z (cos(b z) - i sin(b z)))
et finalement :
(R21x) vx = vg (1 - e-b z cos(b z))
(R21y) vy = vg e-b z sin(b z)
La Figure 2 ci-dessus illustre la variation des composantes vx et vy en fonction de l'Altitude z.
Près du sol (z → 0), on peut faire un développement limité d'ordre 1 (sin(b z) → b z ; cos(b z) → 1 ; e-b z → 1 - b z) et les relations (R21x)(R21y) induisent :
(R22) vx et vy → vg b z
ce qui donne un déphasage théorique de 45° entre le Vent au sol et le Vent géostrophique.
Ce déphasage diminue progressivement quand l'Altitude augmente, formant ainsi une spirale logarithmique, dite "spirale d'Ekman" (voir Figure 2).
L'épaisseur (zg) de la Couche limite atmosphérique est définie comme la première Altitude z à laquelle le champ de vitesses vh s'aligne sur le champ géostrophique vg (axe (x)), ce qui donne :
(R23) zg = π/b = π (K/(Ω sin(Φ)))1/2
Pour une région de Latitude Φ = 45° et un coefficient K de viscosité turbulente de l'ordre de 10 m2/s, cette épaisseur vaut environ zg = 1400 m.
A l'Altitude zg, on a donc : vh = (1 + e-π) vg et le Vent synoptique a une intensité quasiment égale à celle du Vent géostrophique.
Au-dessus de cette Altitude théorique, le modèle d'Ekman est considéré comme non valide.
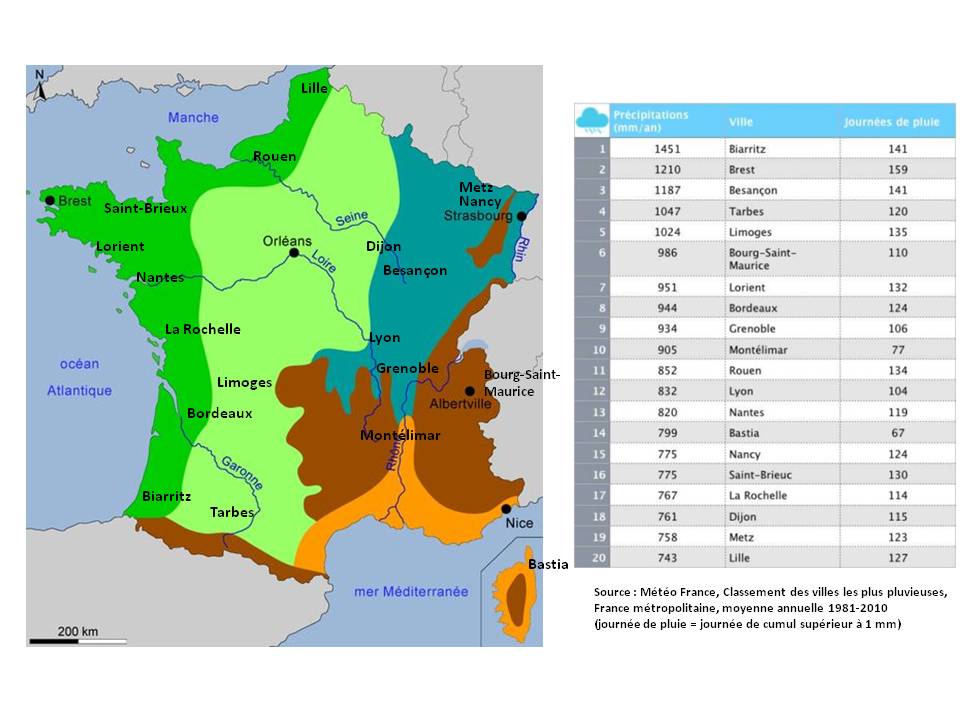
La France métropolitaine bénéficie d'un climat tempéré avec des pluies réparties toute l'année et des températures relativement douces. Ces caractéristiques sont dues à la latitude moyenne et à la dominance des vents venus de l'Atlantique. En première approche (voir carte ci-dessus), on distingue cinq grands types de climats en France métropolitaine (cf [Météo-France, Le climat]) :
Le tableau ci-dessus présente le classement des 20 villes de France métropolitaine les plus pluvieuses (cf [CNEWS, Voici]). Biarritz, Brest et Besançon sont largement en tête.
Le Lexique ci-dessous contient les termes utilisés dans cette page, listés par ordre alphabétique.
Les auteurs cités dans cette page sont mentionnés entre crochets sous la forme [AUTEUR Titre Page].
 Dernière mise à jour de la page : 22 janvier 2026.
Dernière mise à jour de la page : 22 janvier 2026.