Bélier hydraulique

Annexe : Equations d'un fluide dans une canalisation ( Chapitre Précédent / Suivant )

Préambule ( Paragraphe Début / Suivant )

Deux équations générales permettent de calculer la vitesse (v) d'un fluide dans une canalisation, en fonction du temps (t) et de l'abscisse curviligne (x) de cette canalisation : l'équation de continuité et l'équation du mouvement.
Nous appliquons ensuite ces équations à cinq cas pratiques : colonne motrice constante, colonne résistante constante, cheminée d'équilibre, pompe et turbine.
Nous donnons enfin quelques éléments clefs pour dimensionner une turbomachine.

Remarques :
- Dans ce chapitre, nous nous référons aux Figures de ce chapitre, Notations.
- Les auteurs cités sont mentionnés entre crochets sous la forme [AUTEUR Titre Page]. Voir Bibliographie.

Sommaire de ce chapitre ( Paragraphe Précédent / Suivant )

0. Figures
1. Equation de continuité
2. Equation du mouvement
3. Equation du Bernoulli généralisée
4. Applications pratiques
   1. Colonne motrice constante
   2. Colonne résistante constante
   3. Cheminée d'équilibre
   4. Pompe
   5. Turbine
5. Dimensionnement d'une turbomachine
   1. Vitesse spécifique
   2. Diamètre spécifique
   3. Utilisation pratique

0. Figures ( Paragraphe Précédent / Suivant )

Avertissement : pour afficher la dernière mise à jour des figures suivantes, pensez à supprimer les "fichiers temporaires" de votre navigateur Internet avant d'accéder à cette page.

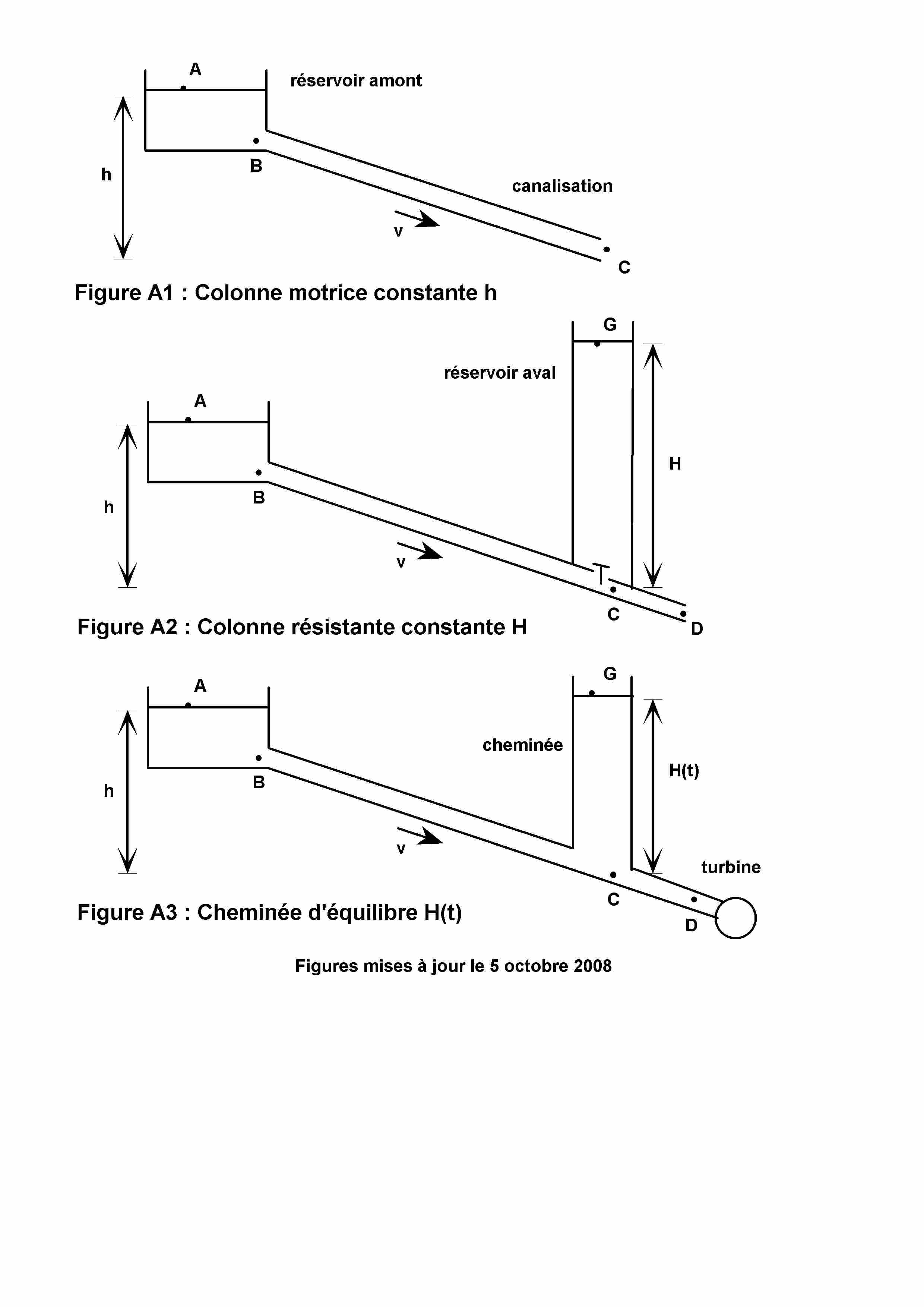
Les quatre Figures ci-dessus montrent chacune un cas pratique de mise en eau d'un système hydraulique.
La Figure A1 (colonne motrice constante) montre le cas d'un réservoir d'eau se vidant à l'air libre par une canalisation, depuis une hauteur h constante.
La Figure A2 (colonne résistante constante) montre le cas d'un réservoir d'eau communiquant à travers un clapet anti-retour avec un réservoir aval de hauteur H constante.
La Figure A3 (cheminée d'équilibre) montre le cas d'un réservoir d'eau alimentant une turbine avale, elle-même protégée juste avant par une cheminée d'équilibre de hauteur H fonction du temps t.
La Figure A4 (pompe ou turbine) montre le cas d'une pompe ou d'une turbine placée entre deux réservoirs.

1. Equation de continuité ( Paragraphe Précédent / Suivant )

Toute canalisation (section droite S) conduisant un fluide continu (sans trous d'air, masse volumique r, pression p) peut être assimilée à un filet de courant en écoulement unidimensionnel d'abscisse curviligne (x).
L'équation de continuité traduit le principe de conservation de la masse du fluide. L'augmentation de masse (dm), pendant un certain temps (dt), du fluide contenu dans un volume fixe (S dx) est égale à la masse du fluide qui y entre, diminuée de la masse qui en sort.
Le premier membre de cette équation (augmentation de masse) s'écrit donc :
    (dm/dt) dt = (d(r S dx)/dt) dt = (d(r S)/dt) dx dt
Et le second membre (différence de masses) s'écrit :
    r S v dt - [ r S v dt + (d(r S v dt)/dx) dx ] = -(d(r S v)/dx) dt dx
D'où l'équation de continuité [COM 207][SOU 27][OUZ 47][FRE 3] :

Cette équation signifie qu'une variation dans le temps de la masse linéique du fluide (r S) correspond à une variation égale et opposée, dans l'espace, du débit massique (r S v).

Remarque 1 : l'équation (A1) est valable, que le fluide soit :
- parfait (forces de viscosité nulles [OUZ 5]) ou non (fluide visqueux) ;
- incompressible (r indépendant de x et de t [OUZ 49]) ou non ;
- en mouvement permanent (r, p et v indépendants de t [OUZ 41]) ou non (instationnaire).

Remarque 2 : l'équation (A1) se ramène à la conservation du débit massique (qm = r S v) en tout point (x) de la canalisation [OUZ 49] pour, notamment, les deux cas particuliers suivants :
- cas d'un coup de bélier dit "de masse" (S et r indépendants de t) ;
- cas d'une canalisation indéformable (S indépendant de t) conduisant un fluide en mouvement permanent (r indépendant de t).

En développant l'équation (A1), on trouve l'équation équivalente :
(A2)    r dS/dt + S dr/dt + r S dv/dx + r v dS/dx + S v dr/dx = 0

2. Equation du mouvement ( Paragraphe Précédent / Suivant )

L'équation générale du mouvement de toute particule d'un fluide non visqueux, incompressible ou non, s'écrit vectoriellement [OUZ 90] :
    Γ = F - (1/r) grad(p)
où :
    Γ est le vecteur accélération
    F est la résultante des forces actives appliquées à l'unité de masse
    "grad()" est l'opérateur "gradient"
L'accélération Γ de cette particule est par ailleurs la dérivée particulaire du vecteur vitesse v par rapport au temps t, c'est-à-dire la dérivée prise en suivant le mouvement de la particule le long de sa trajectoire [OUZ 43]. Cette accélération s'écrit vectoriellement [OUZ 56] :
    Γ = dv/dt + (1/2) grad(v²) + rot(v) x v
où :
    "rot()" est l'opérateur "rotationnel"
    "x" est l'opérateur "produit vectoriel"

En supposant que les forces de volume dérivent uniquement du champ de pesanteur terrestre (accélération g et altitude z), on a de plus l'équation :
    F = - grad(ψ) = -grad(g z)
ψ est le potentiel gravitationnel issu de l'Equation de Poisson (voir chapitre Relativité - Lexique) tel que : ψ = -G M_Terre / (R_Terre + z) = -(G M_Terre / R_Terre) (1 + z/R_Terre)^-1, et qui s'approxime en : ψ = -(G M_Terre / R_Terre) + g z dans le cas de faibles altitudes z par rapport au rayon de la Terre (z << R_Terre).
D'où l'expression générale du mouvement d'un fluide parfait dans le champ de pesanteur terrestre [OUZ 91][FRE 3] :

Pour un liquide en mouvement non permanent, il est généralement admis que la masse volumique (r) est fonction du temps (t) mais pas des coordonnées spatiales [FRE 3].
Dans ce cas, en posant X la charge de l'écoulement telle que :

alors l'équation (A3) s'écrit :
(A3')    dv/dt + rot(v) x v + (1/r) grad(X) = 0
avec :
(A6)    dr/dx = 0

Remarques :
- La charge de l'écoulement (X) correspond à l'énergie du fluide par unité de volume et se décompose en trois termes :
    - l'énergie potentielle de pression (p), ou pression statique, qui est la pression à l'intérieur du fluide ;
    - l'énergie potentielle de situation (r g z), ou pression de pesanteur, qui est liée à l'altitude (z) ;
    - l'énergie cinétique ( (1/2) r (v²) ), ou pression dynamique, ou pression cinétique, qui est liée à la vitesse (v) du fluide.
- En pratique, toute canalisation n'est pas rigoureusement assimilable à un filet de courant. Pour tenir compte de la répartition de la vitesse dans la section, le dernier terme de l'équation (A4) relatif à l'énergie cinétique est parfois corrigé d'un coefficient multiplicateur ALPHA supérieur à 1 [OUZ 100, 226].

En intégrant l'équation (A3') le long d'une ligne de courant, à un instant donné (dt = 0) où le fluide est supposé "figé" et le terme dv/dt connu en tout point, et en remarquant que dans ce cas le vecteur dx est perpendiculaire au vecteur (rot(v) x v), alors cette équation se simplifie en l'équation de Bernoulli [OUZ 115] :

Remarque : l'équation (A3'') est valable, que le mouvement soit rotationnel (rot(v) non nul) ou irrotationnel (rot(v) nul).

* En régime permanent (dv/dt = 0), l'équation (A3'') devient [OUZ 92] :
(A7)    X = Constante(x)

* En régime non permanent (dv/dt ≠ 0), on considère le cas où la vitesse (v) du fluide ne subit pas de modification trop rapide (coup de bélier dit "de masse"). Les variations de pression (p) du fluide sont alors lentes, ce qui autorise de considérer que la canalisation est indéformable et la masse volumique constante [FRE 3].
Cela s'écrit :
(A8)    dS/dt = 0
(A9)    dr/dt = 0
Par ailleurs, dans le cas particulier d'une canalisation de section (S) constante, on a :
(A10)    dS/dx = 0
En remplaçant les égalités (A6),(A8),(A9) et (A10) dans l'équation de continuité (A2), il vient alors :
(A11)    r S dv/dx = 0
La vitesse (v) qui était, a priori, fonction du temps (t) et de l'abscisse curviligne (x), ne dépend plus, sous les conditions précitées, que du temps (t). Il en est de même pour sa dérivée temporelle (dv / dt).
L'équation (A3'') devient alors [OUZ 116] :
(A12)    r (dv/dt) x + X = Constante(x)

3. Equation du Bernoulli généralisée ( Paragraphe Précédent / Suivant )

Les équations (A7')(A12') se généralisent ensuite pour tenir compte de trois variations de charge supplémentaires :

* Perte de charge singulière (Xs) due aux incidents de parcours du fluide le long de la canalisation (évasement/rétrécissement brusque, coude, clapet, vanne, etc.) [OUZ 140] :

où f8 est le coefficient global de perte de charge singulière, tenant compte de toutes les pertes de charge singulière relatives aux incidents de parcours du fluide dans la canalisation.
Dans le cas d'un changement de section (évasement ou rétrécissement), v est la vitesse débitante dans la plus petite des deux sections.

* Perte de charge linéaire (Xl) due aux forces de viscosité (frottement) [OUZ 177] :

où u est le coefficient de perte de charge linéaire de la canalisation, L sa longueur et D son diamètre intérieur.
Dans le cas d'un changement de section, il convient de sommer les pertes de charge linéaires relatives à chaque tronçon L1 et L2 de la canalisation : Xl = (1/2) u r ( (L1/D1) v1² + (L2/D2) v2² )

* Gain ou perte de charge nette (Xn) due aux machines génératrices (pompe) ou motrices (turbine) présentes dans la canalisation [OUZ 242] :

avec :
Pn = puissance nette de la machine fournie au fluide (Pn = Pa R pour une pompe) ou fournie par le fluide (Pn = Pa / R pour une turbine)
Pa = puissance sur l'arbre de la machine
R = rendement global de la machine (produit des rendements mécanique, volumétrique et hydraulique)
Q = débit volumétrique = S v   en tout point (x) de la canalisation.
Xn / (r g) = Hauteur nette (H_n) ou Hauteur Manométrique Totale en mètre (HMT) de la machine

Cette équation constitue la clef pour résoudre l'essentiel des problèmes d'écoulement dans les réservoirs et leurs canalisations, comme nous allons le voir.

4. Applications pratiques ( Paragraphe Précédent / Suivant )

Cinq cas pratiques de mise en eau d'un système hydraulique sont présentés ci-après : colonne motrice constante, colonne résistante constante, cheminée d'équilibre, pompe et turbine.

4.1. Colonne motrice constante ( Sous-paragraphe Début / Suivant )

Prenons le cas d'un grand réservoir d'eau se vidant à l'air libre à travers une canalisation de section constante (voir Figure A1).
La masse d'eau du réservoir étant importante, son niveau ne varie quasiment pas (hypothèse de colonne motrice constante h).
Si A, B et C désignent les points du fluide situés respectivement au niveau d'eau du réservoir, au début et à la fin de la canalisation, et si v désigne la vitesse du fluide dans la canalisation, les équations s'écrivent :

Régime permanent entre A et B, d'où :
(A17)    XA = XB
avec :
XA = pA + r g zA + (1/2) r (vA²)
XB = pB + r g zB + (1/2) r (v²)
vA = 0 (le réservoir étant de grande section)

Régime non permanent entre B et C, d'où :
(A18)    XB = XC + Xs + Xl + r L (dv/dt)
avec :
    XC = pC + r g zC + (1/2) r (v²)
    Xs + Xl = (1/2) (j - 1) r (v²)
    j = 1 + f8 + u L/D

Le réservoir et l'extrémité C de la canalisation étant à l'air libre, on a par ailleurs :
(A19)    pA = patm
(A19')    pC = patm

D'où l'équation générale du mouvement [LAN 34][OBR 11][BER 65] [REN 4][OUZ 116] :
(A20)    h = zA - zC = (1/2) j (1/g)(v²) + L (1/g)(dv/dt)

Après résolution de cette équation différentielle (voir Théorie - Phase 6), la vitesse (v) est donc une fonction croissante du temps t :
(A21)    v(t) = vm (e^y - 1) / (e^y + 1)
avec :
(A21')    vm = (2 (1/j) g h)^1/2
(A21'')    y = j (vm / L) t + ln[ (1 + v(t = 0) / vm) / (1 - v(t = 0) / vm) ]

Pour un bélier hydraulique, ce résultat modélise bien la phase N°6 d'éjection de l'eau durant l'ouverture complète du clapet de choc (voir Théorie - Phase 6).

4.2. Colonne résistante constante ( Sous-paragraphe Précédent / Suivant )

Reprenons le cas N°1 précédent, mais avec une canalisation qui communique à travers un clapet anti-retour avec un réservoir aval, et non à l'air libre (voir Figure A2).
On suppose que le niveau d'eau (zG) du réservoir aval est constant et supérieur au niveau d'eau (zA) du réservoir amont (hypothèse de colonne résistante constante (H - h)).
A l'instant t = 0, on suppose qu'une vanne ou un clapet situé en aval (point D) de la canalisation se ferme instantanément et que le clapet anti-retour s'ouvre également instantanément.
Les relations (A17)(A18)(A19) du cas N°1 précédent sont alors applicables en y rajoutant la relation suivante :

Régime permanent entre C et G, d'où :
(A40)    XC = XG
avec :
(A40')    XG = pG + r g zG + (1/2) r (vG²)
(A40'')    vG = v (le réservoir aval ayant une section S' = S au point G)

D'où l'équation générale du mouvement [BER 85][REN 25][OBR 27] :
(A22)    H = zG - zC = h - (1/2) j (1/g)(v²) - L (1/g)(dv/dt)

Après résolution de cette équation différentielle (voir Théorie - Phase 3), la vitesse (v) est donc une fonction décroissante de t :
(A23)    v(t) = v'm ( (v(t = 0) / v'm) - tg[ (1/2) j (v'm / L) t ] ) / ( 1 + (v(t = 0) / v'm) tg[ (1/2) j (v'm / L) t ] )
avec :
v'm = ( 2 (1/j) g (H - h) )^1/2

Pour un bélier hydraulique, ce résultat modélise bien la phase N°5 de mise en vitesse de l'eau sans éjection (voir Théorie - Phase 5).
Ce résultat pourrait modéliser également la phase N°3 de refoulement de l'eau dans la cloche à air. Néanmoins, pour être plus proche du phénomène réel (variation rapide de la vitesse et de la pression pendant cette phase), nous opterons pour le modèle du coup de bélier dit "d'ondes", avec comparaison toutefois avec le modèle ci-dessus du coup de bélier dit "de masse" (voir Théorie - Phase 3).

4.3. Cheminée d'équilibre ( Sous-paragraphe Précédent / Suivant )

Reprenons le cas N°2 précédent, mais sans le clapet anti-retour et avec une cheminée d'eau de grande section (S') en guise de réservoir aval (voir Figure A3). Ce dispositif anti-bélier est souvent utilisé dans les circuits de pompage industriel ou dans les centrales hydrauliques afin d'absorber les variations brutales de pression dues à la panne subite d'une pompe ou à l'arrêt d'urgence d'un turbo-alternateur situé en aval sur la canalisation [OUZ 136].
A l'instant t = 0, on suppose qu'une vanne située en D se ferme instantanément.
Les relations (A17)(A18)(A19)(A40)(A40') des cas N°1 et n°2 précédents sont alors applicables en y rajoutant les deux relations :
(A18')    j remplacé par j* = 1 + (f8 + u L/D) Signe[v] (l'écoulement pouvant changer de sens dans la canalisation)
(A40''')    vG = 0 (la cheminée étant de grande section)

D'où l'équation générale du mouvement [FRE 3] :
(A24)    H(t) = zG(t) - zC = h - (1/2)(j* - 1)(1/g)(v²) - L (1/g)(dv/dt)

Par ailleurs, pour un coup de bélier dit "de masse", la conservation du débit massique dans l'ensemble canalisation-cheminée fournit l'équation supplémentaire suivante :
(A25)    r S v = r S' dH/dt

Dans le cas simplifié où les pertes de charge sont négligeables (j* = 1) dans toute la canalisation, l'équation générale du mouvement s'écrit :
(A26)    d2v / dt2 = -(g/L) (S/S') v
Et on trouve alors que la vitesse (v) dans la canalisation est une fonction sinusoidale de t et de période T :
(A27)    v(t) = v(t = 0) cos[ A + t (2 π / T) ] / cos[ A ]
avec :
2 π / T = ( (g/L) (S/S') )^1/2
sin(A) = Ks / K
cos(A) = Kc / K
Ks = H(t = 0) - h
Kc = v(t = 0) ( (L/g)(S/S') )^1/2
K = ( (Ks²) + (Kc²) )^1/2

Pour un bélier hydraulique, ce modèle de cheminée d'équilibre pourrait éventuellement modéliser la phase de refoulement de l'eau de la cloche dans la conduite de refoulement, sous réserve de rendre constante la hauteur H et variable la pression amont (pA), cette dernière diminuant rapidement pendant la détente de l'air dans la cloche. Cette adaptation est étudiée dans un chapitre ad hoc (voir Théorie - Phase 8).

4.4. Pompe ( Sous-paragraphe Précédent / Suivant )

Prenons le cas d'une pompe motorisée qui refoule l'eau dans une canalisation depuis un grand réservoir inférieur (point G en surface) vers un grand réservoir supérieur (point A en surface) (voir Figure A4)

4.4.1. Relations pour une pompe

Les différentes relations sont les suivantes :
    (A28) :
XA = charge au point A = pA + r g zA + (1/2) r vA²
XG = charge au point G = pG + r g zG + (1/2) r vG²
Xs + Xl = pertes de charge singulière + pertes de charge linéaire = (1/2) (j - 1) r v²
j - 1 = f8 + u L/D
f8 = coefficient global de perte de charge singulière dans la canalisation.
L = longueur totale de la canalisation
D = diamètre intérieur de la canalisation
S = section intérieure de la canalisation = (π/4) D²
Q = débit volumique refoulé = S v
Xn = gain de charge nette de la pompe = Pn/Q
Pn = puissance nette de la pompe fournie au fluide
Pa = puissance sur l'arbre de la pompe = Pn/R
R = rendement global de la pompe hors actionneur
Pm = puissance absorbée par le moteur de la pompe = Pa/Rm
Rm = rendement du moteur

Chaque réservoir étant de grande section, on a :
(A29)    vA = vG = 0

Chaque réservoir étant à l'air libre, on a :
(A30)    pressions statiques en A et G : pA = pG = patm

Le sens de l'écoulement va du point G au point A (pompe refoulante). En conséquence, en régime permanent, l'équation généralisée de Bernoulli appliquée à l'eau en mouvement s'écrit :
(A31)    XG + Xn = XA + Xs + Xl

Compte-tenu des relations (A28)(A29)(A30)(A31), la puissance hydraulique (Pn) de la pompe est alors la suivante :
(A32)    Pn = Q r g HMT_pompe
avec :
(A33)    HMT_pompe = Hauteur Manométrique Totale en mètre = (zA - zG) + (1/2) (1/g) (j - 1) (Q/S)²

Dans le cas fréquent où vG = 0 et pG = patm, les constructeurs de pompes présentent HMT_pompe sous une forme équivalente :
HMT_pompe = P_gravitaire + P_dynamique + P_service
avec :
P_gravitaire en mètre = zA - zG
    P_gravitaire est la pression de pesanteur produite par la différence d'altitude entre les points A et G.
P_dynamique en mètre = (1/2) (1/g) (j - 1) (Q/S)²
    P_dynamique est une pression cinétique subie, produite par les pertes de charge Xl et Xs.
    P_dynamique se détermine souvent sur une abaque en fonction de Q et de D par tranche de longueur L (1 m ou 100 m selon l'abaque).
    Aux pertes de charge singulière près, P_dynamique vaut k L avec k = (8 / π²) (1/g) u Q²/D⁵
    Pour des vitesses v inférieures à 2 m/s et des diamètres D supérieurs à 2", k peut être pris à 0,1 approximativement.
P_service en mètre (ou pression de sortie ou pression d'utilisation ou pression utile)
    P_service, quand elle existe, est la pression souhaitée (statique et cinétique), produite en sortie de la canalisation (point A) :
    P_service en mètre = (pA - patm)/(r g) + (1/2) (1/g) (vA)² = 10 m pour chaque tranche de pression de 1 bar
    La pression pA dépend de la pression statique au point A. Elle vaut pA = patm   quand la canalisation débouche à l'air libre.
    La vitesse vA dépend de la section (SA) au point A. Elle vaut vA = Q / SA   compte-tenu de la conservation du débit massique (qm = r Q) dans la canalisation. Elle vaut vA = 0   quand SA est très grand.
Dans le cas d'une lance d'incendie pour pompiers, on voit donc qu'augmenter la vitesse d'éjection en sortie de lance, la hauteur de la lance, le débit volumique ou les pertes de charge exige que la pompe fournisse une puissance plus élevée.

On calcule ensuite la puissance absorbée (Pm) par le moteur de la pompe, comme suit :
(A34)    Pm = (1/R) (1/Rm) Pn
Compte-tenu des relations (A32)(A34), les constructeurs de pompes présentent souvent la formule équivalente suivante : Pm_{en kW} = (1 / (R Rm)) (1 / 367) Q_{en m³/heure} HMT_{en m}

4.4.2. Application numérique (puissance de la pompe)

Installation : zA - zG = 15 m ; L_refoulement = 120 m ; L_aspiration = 4 m ; D = 0,019 m ;
Pompe : Q = 2 m³/heure = (2 / 3600) m³/s ; f8 = 15 (vannes, coudes, raccords, clapet anti-retour, crépine) ; R = 0,6 ; Rm = 0,9 (cas d'une pompe électrique)
Constantes : u = 0,02 ; r = 1000 kg.m^-3 pour de l'eau ; g = 9,81 m.s^-2 à Paris
L = L_refoulement + L_aspiration = 124 m
j - 1 = f8 + u L/D = 146
P_gravitaire en mètre = zA - zG = 15 m
P_dynamique en mètre = (1/2) (1/g) (j - 1) (Q/S)² = 29 m
P_service en mètre = 0 m (cas d'un refoulement en partie basse d'un grand réservoir)
HMT_pompe = P_gravitaire + P_dynamique + P_service = 44 m
Pn = Q r g HMT_pompe = 240 W
Pm = (1/R) (1/Rm) Pn = 450 W

4.4.3. Cavitation dans une pompe

Si E désigne le point d'entrée de la pompe sur l'axe de sa bride d'aspiration, il peut y avoir cavitation en E lorsque la pression totale (ptE) devient inférieure à la pression de vapeur saturante de l'eau (p_V) selon la relation suivante :
    (A35) NPSH_d < NPSH_r
avec :
    (A35') :
NPSH (Net Positive Suction Head) = hauteur de charge nette absolue à l'aspiration (en mètre)
NPSH_d = NPSH disponible = marge de pression totale au-dessus de p_V disponible au point E = (ptE - p_V) / (r g)   par définition
ptE = pression totale (statique et cinétique) au point E = pE + (1/2) r vE²
p_V = pression de vapeur saturante de l'eau = {1,23 ; 4,24 ; 19,9 ; 70,1 ; 101,325} en kPa pour de l'eau à la pression atmosphérique et pour des températures respectives de {10 ; 30 ; 60 ; 90 ; 100} en °C
NPSH_r = NPSH requis par la constructeur de la pompe. NPSH_r est donné en fonction du débit volumique Q, pour un fluide donné (masse volumique et viscosité) et pour une pompe donnée fonctionnant à une vitesse de rotation donnée.

En régime permanent, l'équation généralisée de Bernoulli appliquée à l'eau en mouvement allant du point G du réservoir au point E de la pompe, s'écrit :
(A36)    XG = XE + (Xs + Xl)_{entre G et E}
avec :
XG = charge au point G = pG + r g zG + (1/2) r vG²
XE = charge au point E = pE + r g zE + (1/2) r vE²
(Xs + Xl)_{entre G et E} = pertes de charge (singulière et linéaire) entre G et E

Le réservoir étant de grande section et à l'air libre, on a :
(A37)    vG = 0
(A38)    pG = patm

Compte-tenu des relations (A35')(A36)(A37)(A38), le NPSH disponible se calcule alors comme suit :
(A39)    NPSH_d pour une pompe = (patm - p_V)/(r g) - (zE - zG) - (Xs + Xl)_{entre G et E} /(r g)
Attention : la hauteur d'aspiration (zE - zG) est positive pour une pompe montée en aspiration et négative pour une pompe montée en charge.

La cavitation survient si la relation (A35) est vérifiée.
On constate que la cavitation est d'autant plus évitée que :
- la température de l'eau est basse (p_V plus petit),
- la hauteur d'aspiration est petite, voire négative (pompe montée en charge),
- les pertes de charges entre G et E sont petites (notamment en augmentant le diamètre de la canalisation à l'aspiration),
- le débit volumique (Q) est réduit (NPSH_r plus petit).

4.4.4. Application numérique (cavitation dans une pompe)

Installation : zE - zG = 2 m ; D = 0,019 m
Pompe : Q = 2 m³/heure = (2 / 3600) m³/s ; f8 = 13 (vannes, clapet anti-retour, crépine) ; NPSH_r du constructeur = 1,10 + 101250 Q²
Constantes : r = 1000 kg.m^-3 pour de l'eau ; patm = 101,325 kPa ; p_V = 4,24 kPa pour de l'eau à 30°C et à pression atmosphérique ; g = 9,81 m.s^-2 à Paris
(Xs + Xl)_{entre G et E} = (1/2) f8 (Q/S)² = 25,0 Pa
NPSH_d = (patm - p_V) / (r g) + (zG - zE) - (Xs + Xl)_{entre G et E} / (r g) = 7,9 m
lequel est supérieur à NPSH_r = 1,10 + 101250 Q² = 1,13 m
Donc, l'écoulement en aspiration de pompe ne subit pas de cavitation.

4.5. Turbine ( Sous-paragraphe Précédent / Début )

Prenons le cas d'une turbine placée entre un grand réservoir supérieur (point A en surface) et un grand réservoir inférieur (point G en surface) (voir Figure A4)

4.5.1. Relations pour une turbine

Les différentes relations sont les suivantes :
    (A40) :
XA = charge au point A = pA + r g zA + (1/2) r (vA²)
XG = charge au point G = pG + r g zG + (1/2) r (vG²)
Xs + Xl = pertes de charge singulière + pertes de charge linéaire = (1/2) (j - 1) r v²
j - 1 = f8 + u L/D
f8 = coefficient global de perte de charge singulière dans la canalisation.
L = longueur totale de la canalisation
D = diamètre intérieur de la canalisation
S = section intérieure de la canalisation = (π/4) D²
Q = débit volumique produit = S v
Xn = perte de charge nette de la turbine = Pn/Q
Pn = puissance nette de la turbine fournie par le fluide
Pa = puissance sur l'arbre de la turbine = Pn R
R = rendement global de la turbine

Chaque réservoir étant de grande section, on a :
(A41)    vA = vG = 0

Chaque réservoir étant à l'air libre, on a :
(A42)    pressions statiques en A et G : pA = pG = patm

Le sens de l'écoulement va du point A au point G. En conséquence, en régime permanent, l'équation généralisée de Bernoulli appliquée à l'eau en mouvement s'écrit :
(A43)    XA = XG + Xn + Xs + Xl

Compte-tenu des relations (A40)(A41)(A42)(A43), la puissance hydraulique (Pn) de la turbine est alors la suivante :
(A44)    Pn = Q r g HMT_turbine
avec :
(A45)    HMT_turbine = Hauteur Manométrique Totale en mètre = (zA - zG) - (1/2) (1/g) (j - 1) (Q/S)²

On calcule ensuite la puissance (Pa) fournie sur l'arbre de la turbine, comme suit :
(A46)    Pa = Pn R

On constate que cette puissance ne dépend pas de la position de la turbine au sein de la canalisation, la vitesse de l'écoulement (v = Q/S) étant la même dans toute la canalisation.

4.5.2. Cavitation dans une turbine

La cavitation est un phénomène d'érosion en sortie de toute turbine, qu'elle soit à réaction (type Francis ou Kaplan ou pompe inversée) ou à action (type Pelton ou Crossflow).
On examine le cas courant d'une turbine à réaction [NBTEL][GUITON Cavitation][PACER].
Si E désigne le centre de la roue, point de sortie de la turbine et aussi point d'entrée du diffuseur, il peut y avoir cavitation en E lorsque la pression totale (ptE) devient inférieure à la pression de vapeur saturante de l'eau (p_V) selon la relation suivante :
    (A50) σ_T < σ_Tc
avec :
    (A51) σ_T = NPSH_d / HMT_turbine = coefficient de Thoma au point E qui est sans dimension
Attention : σ_T est souvent confondu avec le nombre de cavitation σ = (p - p_V) / ( (1/2) r v² )
NPSH_d = NPSH disponible au point E (voir relation (A35') ci-dessus au paragraphe Pompe - Cavitation)
HMT_turbine = Hauteur Manométrique Totale en mètre (voir relation (A45) ci-dessus)
σ_Tc = coefficent de Thoma critique, donné par le constructeur de la turbine au point E = ( (patm - pE)/(r g) + (zG - zE) ) / HMT_turbine
σ_Tc varie de 0,1 à 0,64 pour les turbines Francis et de 0,4 à 1,5 pour les turbines Kaplan.

En régime permanent, l'équation généralisée de Bernoulli appliquée à l'eau en mouvement allant du point E de la turbine au point G du réservoir, s'écrit :
(A52)    XE = XG + (Xs + Xl)_{entre E et G}
avec :
XE = charge au point E = pE + r g zE + (1/2) r vE²
XG = charge au point G = pG + r g zG + (1/2) r vG²
(Xs + Xl)_{entre E et G} = pertes de charge (singulière et linéaire) entre E et G

Le réservoir étant de grande section et à l'air libre, on a :
(A53)    vG = 0
(A54)    pG = patm

Compte-tenu des relations (A35')(A52)(A53)(A54), le NPSH disponible se calcule alors comme suit :
(A55)    NPSH_d pour une turbine à réaction = (patm - p_V)/(r g) - (zE - zG) + (Xs + Xl)_{entre E et G} /(r g)
Les pertes de charges (Xs + Xl)_{entre E et G} étant souvent négligeables, la relation se simplifie en :
(A56)    NPSH_d pour une turbine à réaction = (patm - p_V)/(r g) - (zE - zG)
Attention : la hauteur d'aspiration (zE - zG), généralement positive, peut être négative (turbine installée en-dessous du niveau de restitution).

On calcule ensuite σ_T selon la relation (A51).

La cavitation survient si la relation (A50) est vérifiée.
On constate que la cavitation est d'autant plus évitée que :
- la température de l'eau est basse (p_V plus petit),
- la hauteur d'aspiration est petite, voire négative,
- la puissance nette (Pn) est réduite (HMT_turbine plus petit).

5. Dimensionnement d'une turbomachine ( Paragraphe Précédent / Début )

Le dimensionnement d'une turbomachine (pompe, turbine, ventilateur ou compresseur) fait appel a deux concepts issus de l'étude des lois de similitude des turbomachines : la vitesse spécifique et le diamètre spécifique.
Ils sont très utiles pour la conception de machines similaires (homothétiques) appartenant à une même famille et constituent une base pour le classement de chaque appareil.

5.1. Vitesse spécifique

Tous les traités de turbomachines étudient la variation de la forme du rotor en fonction de la "vitesse spécifique" définie comme suit [OUZ Contributions][EDF] :

(A60)    Ω ou C_v ou N_s = coefficient de vitesse angulaire (en rad, et considéré usuellement sans dimension) = ω_rad/s Q_m³/s^1/2 / (g H_m)^3/4
avec :
    ω = vitesse angulaire du rotor (en rad/s)
    Q = débit volumique (en m³/s)
    g = 9,81 m.s^-2 à Paris
    H = Hauteur nette de la machine (en m)
Le coefficient Ω est indépendant des dimensions de la machine et de la masse volumique du fluide [EDF].

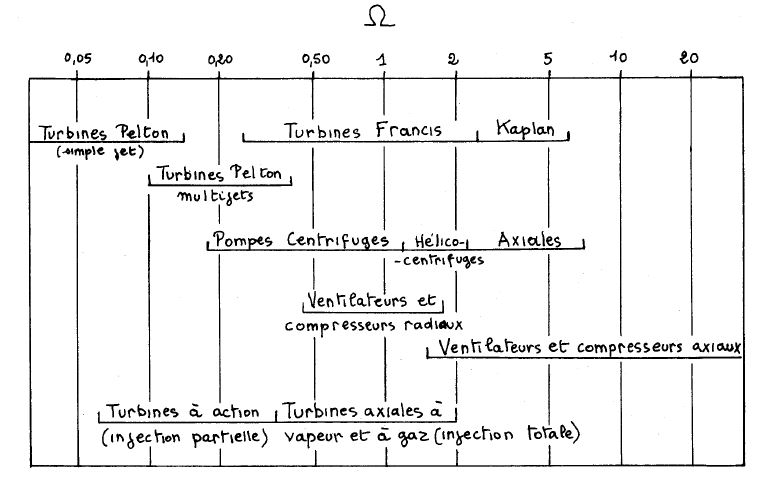
L'expérience montre que chaque famille de turbomachines, caractérisée par la forme de son rotor, a son maximum de rendement dans une gamme très étroite de valeurs de Ω, et sa connaissance permet donc de choisir le type de machine à employer [CAI]. La Figure 1 ci-dessus illustre la correspondance entre Ω et le type de turbomachine au point de rendement maximal [CAI][OUZ Contributions].
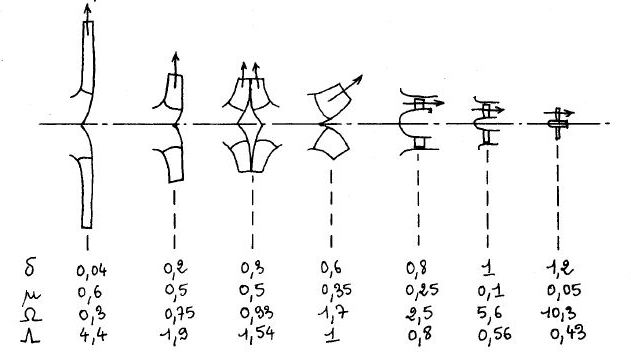
La forme géométrique du rotor à utiliser pour se situer dans un domaine de bon rendement est également déterminée à partir de la connaissance de Ω [CAI]. La Figure 2 ci-dessus illustre la correspondance entre Ω et la forme géométrique du rotor des pompes, ventilateurs et compresseurs [CAI][OUZ Contributions].

De façon équivalente à Ω, sont définis deux autres coefficients, l'un en débit, l'autre en puissance [OUZ Contributions] :

(A61)    n_sq = nombre de tours spécifique de débit (ou fonction de Brauer) = n_tr/min Q_m³/s^1/2 / (H_m)^3/4
avec :
    n = nombre de tours par minute du rotor = (30 / π) ω
Conversion : Ω = n_sq (π / 30) / g^3/4 = (1/ 53) n_sq

En notation américaine, on a l'équivalence suivante :
(A62)    N_sq = nombre de tours spécifique de débit = N_tr/min Q_ft³/s^1/2 / (H_ft)^3/4
avec :
    N = nombre de tours par minute du rotor = (30 / π) ω
Conversion (avec 1 ft = 0,305 m) : Ω = N_sq (π / 30) (0,305)^3/4 / g^3/4 = (1/ 129) N_sq

(A63)    n_sp = nombre de tours spécifique de puissance (ou fonction de Cammerer) = n_tr/min P_ch^1/2 / (H_m)^5/4
avec :
    n = nombre de tours par minute du rotor = (30 / π) ω
    P = puissance sur l'arbre de la machine en chevaux (1 ch = 735 W)
Compte-tenu de la relation (A15) : P_n = r Q g H_n, en supposant que le fluide est de l'eau froide de masse volumique r = 1000 kg/m³ et en négligeant l'influence du rendement de la machine (P_n = P), on a la conversion suivante :
Conversion : Ω = n_sp (π / 30) (735 / r)^1/2 / g^5/4 = (1/ 193,4) n_sp

Attention : il existe dans le domaine industriel d'autres coefficients équivalents ayant une définition différente.

5.2. Diamètre spécifique

Le "diamètre spécifique" d'une turbomachine est défini comme suit [OUZ contributions] :

(A70)    Λ = coefficient de rayon (sans dimension) = R_m (g H_m)^1/4 / Q_m³/s^1/2
    ou   D_s = coefficient de diamètre spécifique (sans dimension) = D_m (g H_m)^1/4 / Q_m³/s^1/2 = 2 Λ
avec :
    R = rayon extérieur du rotor (en m)
    D = diamètre extérieur du rotor (en m) = 2 R
    g = 9,81 m.s^-2 à Paris
    H = Hauteur nette de la machine (en m)
    Q = débit volumique (en m³/s)
Le coefficient Λ est indépendant de la vitesse de rotation de la machine et de la masse volumique du fluide.

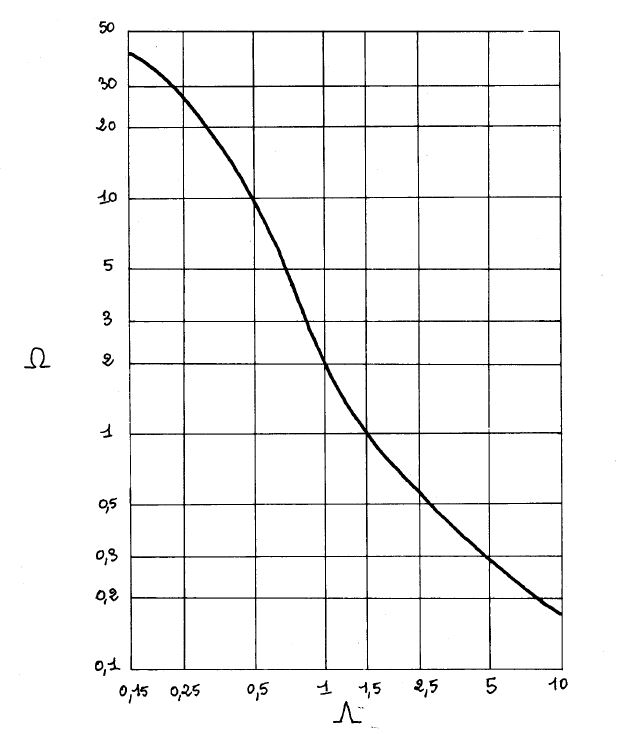
Pour une turbomachine située à son rendement maximum, le coefficient Λ est relié au coefficient Ω selon le diagramme (ou courbe) de Cordier [COR, pp.337-340] revu par Csanady [CSA] puis par Lewis [LEW, p.17] (voir Figure 3 ci-dessus tirée de [OUZ Contributions, p.75]).
Ce diagramme est une courbe moyenne empirique issue des mesures réalisées au début des années 1950 sur un très grand nombre de machines tournantes.
La connaissance de Ω permet le calcul de Λ. Formule approximative : Λ = (1/5)(1 + 8/Ω)
Attention : il existe plusieurs courbes de Cordier en fonction des axes (abscisse et ordonnée), des définitions pour la vitesse spécifique et le diamètre spécifique, et aussi de leurs unités.

De façon équivalente à Λ, sont définis deux autres coefficients, l'un en débit, l'autre en puissance [OUZ Contributions] :

(A71)    d_sq = diamètre spécifique de débit = d_m (H_m)^1/4 / Q_m³/s^1/2
avec :
    d = diamètre extérieur du rotor (en m)
Conversion : Λ = d_sq (1/2) g^1/4 = 0,885 d_sq

En notation américaine, on a l'équivalence suivante :
(A72)    D_sq = diamètre spécifique de débit = D_ft (H_ft)^1/4 / Q_ft³/s^1/2
avec :
    D = diamètre extérieur du rotor (en ft)
Conversion (avec 1 ft = 0,305 m) : Λ = D_sq (1/2) (0,305)^-1/4 g^1/4 = 1,19 D_sq

(A73)    d_sp = diamètre spécifique de puissance = d_m (H_m)^3/4 / P_ch^1/2
avec :
    d = diamètre extérieur du rotor (en m)
    P = puissance sur l'arbre de la machine en chevaux (1 ch = 735 W)
Compte-tenu de la relation (A15) : P_n = r Q g H_n, en supposant que le fluide est de l'eau froide de masse volumique r = 1000 kg/m³ et en négligeant l'influence du rendement de la machine (P_n = P), on a la conversion suivante :
Conversion : Λ = d_sp (1/2) g^3/4 / (735 / r)^1/2 = 3,23 d_sp

Attention : il existe dans le domaine industriel d'autres coefficients équivalents ayant une définition différente.

5.3. Utilisation pratique

En pratique, pour dimensionner une turbomachine en projet [OUZ Contributions][CAI] :
- On calcule le coefficient Ω en fonction des conditions d'utilisation ω, Q et H (relation (A60)), ce qui donne la forme géométrique du rotor à utiliser (Figure 2).
- On calcule ensuite le coefficient Λ (cf courbe de Cordier ou sa formule approximative), ce qui donne le rayon extérieur R du rotor (relation (A70)).

En général, on a intérêt à choisir la vitesse de rotation la plus élevée possible, Ω étant proportionnelle à ω, ce qui diminue le coefficient de rayon Λ et, par conséquent, les dimensions de la machine projetée et son prix de revient [OUZ Contributions].

Copyright © 2005 Régis Petit.               Dernière mise à jour de la page : 11 août 2024.